Графическое изображение теории производства
Теория производства, изложенная в этой главе Теория производства и предельных продуктов, может быть представлена графически. В табл. 26-2 приведен числовой пример простой функции производства, характеризующей отношение между затратами двух факторов производства (труда и капитала) и выпуском продукции. Таблица составлена в форме расчерченного в двух направлениях квадрата, она напоминает таблицу игр между бейсбольными командами или карту, показывающую расстояние в милях между различными городами.
В функции производства обобщаются результаты различных технических процессов:
Таблица 26-2
Функция производства устанавливает соотношения между изменяющимися сочетаниями затрат труда и капитала и количеством выпускаемой продукции. Если вы располагаете 3 единицами капитала и 2 единицами труда, инженер скажет вам, что максимально возможный выпуск продукции будет составлять 346 единиц. Заметьте, что можно различным образом изготовить 346 и 490 единиц продукции.
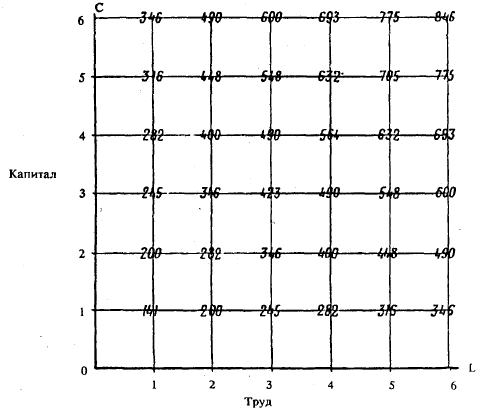
На вертикальной оси нанесены данные, характеризующие величину используемого капитала, от 1 единицы и до 6 единиц. На горизонтальной оси указывается количество применяемого труда, от 1 единицы до 6 единиц. Размеры выпуска продукции при использовании определенного сочетания между капиталом и трудом показаны внутри квадрата на месте пересечения соответствующих строки и колонки.
Если вы хотите точно определить выпуск продукции при наличии 5 единиц капитала и 2 единиц труда, вы отсчитываете по вертикальной оси 5 единиц капитала, а затем по горизонтальной — 2 единицы труда. Ответ можно видеть на пересечении соответствующих строки и столбца — 448 единиц продукта. Аналогичным образом мы находим, что 3 единицы капитала и 6 единиц труда произведут 600 единиц продукции. Таким образом, для любого сочетания труда и капитала функция производства покажет максимально возможный объем выпускаемой продукции (разумеется, при условии использования наилучших методов производства в соответствии с указаниями технического специалиста).
Закон убывающего физического объема предельного продукта
Закон убывающей доходности может быть хорошо проиллюстрирован данными табл. 26-2.
Во-первых, напомним, что мы назвали «физическим объемом предельного продукта труда» дополнительную продукцию, получаемую в результате использования одной добавочной единицы труда при неизменной величине применяемого капитала. Для любой точки в табл. 26-2 физический объем предельного продукта труда можно исчислить путем вычитания данного числа (представляющего размеры выпускаемой продукции при соответствующих затратах факторов производства) из числа, расположенного справа от него в том же ряду. Так, если имеются 2 единицы капитала и 4 единицы труда, физический объем предельного продукта для дополнительного рабочего составляет 48 единиц, или 448 единиц минус 400 единиц.
Под «физическим объемом предельного продукта капитала» мы понимаем, разумеется, дополнительный продукт, полученный в результате использования добавочной единицы капитала; при этом количество применяемого труда остается неизменным. Для определения физического объема предельного продукта капитала необходимо сравнить между собой смежные цифры в данной графе. Так, если имеются 2 единицы капитала и 4 единицы труда, то физический объем предельного продукта капитала составляет 90 единиц, или 490 единиц минус 400 единиц. Читатель должен уметь определять физический объем предельного продукта труда или капитала для любой точки, нанесенной на таблице.
Определив то, что мы называем физическим объемом предельного продукта, производимого с помощью данного фактора производства, мы теперь можем сформулировать закон убывающей доходности по-новому.
Если мы расширяем использование одного какого-либо фактора производства и сохраняем при этом неизменными затраты всех остальных факторов, то физический объем предельного продукта, производимого с помощью переменных затрат указанного фактора, станет, по крайней мере начиная с какой-то определенной стадии, убывать.
Это положение можно иллюстрировать следующим примером. Предположите в табл. 26-2 величину капитала неизменной, рассматривая тем самым лишь те данные, которые относятся к одной и той же строке, — допустим, например, что размеры капитала составляют 2 единицы. Теперь давайте увеличим количество используемого труда с 1 до 2 единиц, с 2 до 3 единиц и так далее. Как будут изменяться размеры выпускаемой продукции на каждой из этих стадий?
Поскольку количество труда возрастает с 1 до 2 единиц, продукт увеличивается с 200 до 282 единиц, или на 82 единицы. Но последующее добавление еще 1 единицы труда прибавит только 64 единицы, или 346-282. Началось постепенное убывание доходности. Дальнейшее прибавление к используемому количеству труда по единице будет обеспечивать нам соответственно только 54 единицы, 48 единиц и, наконец, только 42 единицы дополнительной продукции. Читатель может рассмотреть какую-нибудь другую строку и проверить, что закон убывающей доходности сохраняет силу и в этом случае. Он может также проверить следующее обстоятельство: этот же закон остается верным и в том случае, когда количество труда не изменяется, а размеры капитала последовательно увеличиваются. (Проверьте вдоль любой колонки изменения в размерах выпускаемой продукции.)
В этой связи уместно напомнить о приводившейся выше трактовке закона убывающей доходности. В главе 2 убывающая доходность связывалась со следующим фактом: когда один из факторов производства используется в неизменном масштабе, его затраты сокращаются по отношению к увеличивающимся затратам другого фактора. Каждая новая единица переменного фактора производства может взаимодействовать лишь с относительно уменьшающимися затратами постоянного фактора, поэтому естественно ожидать, что и размеры дополнительного продукта должны начать сокращаться.
Если такое рассуждение справедливо для всех случаев, то при увеличении затрат обоих факторов производства в соответствующих пропорциях не должно происходить никакого убывания доходности. Если количество применяемого труда возрастает с 1 до 2 единиц и размеры используемого капитала соответственно увеличиваются с 1 до 2 единиц, то мы должны получить такое же увеличение размеров выпускаемой продукции, как и в случае одновременного увеличения затрат обоих факторов производства с 2 до 3 единиц. Это можно проверить по табл. 26-2. В первом случае выпуск продукции увеличивается с 141 до 282, а во втором случае размеры продукции возрастают с 282 до 423, что составляет расширение производства опять-таки на 141 единицу.
Не всякие функции производства, с которыми мы сталкиваемся в реальной экономической жизни, должны обладать такими особыми свойствами — так называемым «постоянным соотношением между масштабами производства и размерами доходов». Вспомните рассматривавшиеся в главе 2 положения об увеличении доходов по мере расширения производства и об экономии, обеспечиваемой массовым производством.
Кроме того, подобная трактовка закона убывающей доходности, сводящаяся к изменению в пропорциях между затратами отдельных факторов производства, должна привести нас к следующему предположению. Если увеличить размеры капитала, то это приведет к увеличению физического объема предельного продукта труда. Это опять-таки можно проверить по нашей таблице: при использовании 2 единиц капитала 5-я единица труда произведет 48 единиц продукта, а при наличии 3 единиц капитала 5-я единица труда увеличит выпуск продукции на 58 единиц.
Сочетание факторов производства, обеспечивающее наименьшие издержки при данных масштабах производства
Числовые значения функции производства показывают, что инженер не может дать однозначный ответ на вопрос о том, как следует изготовлять данное количество продукции. Существует не один, а несколько способов убить кота. Точно так же и произвести любое заранее заданное количество продукции можно несколькими способами. Так, данные, приведенные в табл. 26-2, свидетельствуют о том, что 346 единиц продукции могут быть произведены любым из способов, указанных в табл. 26-3.
Вы можете и вам следовало бы самостоятельно составить аналогичную таблицу для выпуска продукции, равного 490 единицам или какому-либо другому количеству.
Таблица 26-3
Различные сочетания факторов производства при выпуске одного и того же количества продукции. При производстве одного и того же количества продукции (346 единиц) большее количество труда может быть замещено меньшим количеством капитала. Исчислите общую сумму издержек на заработную плату плюс расходы на приобретение капитала при предположении, что цена труда Pl = 2 долл., а цена капитала Рс = 3 долл. На основе этих расчетов покажите, что при различных сочетаниях указанных факторов производства наименьшие издержки достигаются в точке С. Покажите, что понижение затрат на капитал Рс до 1 долл. за единицу вызывает необходимость замещения труда капиталом, в результате чего вы передвигаетесь вдоль кривой от точки С к точке В.
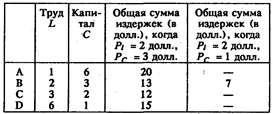
Что касается инженера, то, с его точки зрения, каждая из этих комбинаций затрат различных факторов производства одинаково хороша при изготовлении 346 единиц продукции. Но бухгалтер, который следит за поддержанием прибылей на максимально высоком уровне и обеспечением наименьшей величины издержек производства, знает, что наименьших издержек можно достигнуть с помощью лишь одного из этих четырех сочетаний. Какое из этих четырех сочетаний будет выбрано,— это, конечно, будет зависеть от соотношения между ценами на оба фактора производства.
Предположим, что цена единицы труда составляет 2 долл., а цена единицы капитала — 3 долл.
Тогда сумма затрат на труд и капитал в случае А будет составлять 20 долл. (1x2 долл. + 6x3 долл.), а в случаях В, С и D будет составлять соответственно 13, 12 и 15 долл. При таких заранее заданных ценах не может возникнуть никаких вопросов: способ С является наилучшим способом для производства данного количества продукции!
Как отыскать с помощью графических методов точку наименьших издержек? Во-первых, при изготовлении одного и того же объема продукции факторы производства могут замещать друг друга:
Во-вторых, различные сочетания факторов производства при одном и том же количестве выпускаемой продукции также могут быть изображены графически:
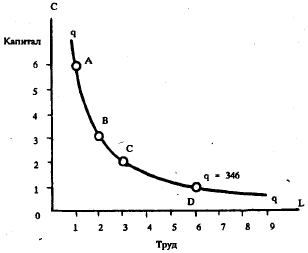
Рис. 128. Кривая равного продукта. Все точки на, кривой равного продукта представляют различные сочетания капитала и труда, которые могут быть использованы для выпуска одного и того же объема, продукции — в 346 единиц.
Если цены на каждый из факторов производства изменяются, то пропорции между ними, определяющие условия равновесия, всегда будут изменяться таким образом, чтобы использовать в меньшей степени тот фактор производства, у которого цена повысилась наиболее значительно в сравнении с ценами остальных факторов. Это в точности соответствует эффекту замещения, описанному в главе 21. Так, например, если цена на труд остается на уровне 2 долл. за единицу, а цена на капитал снижается до 1 долл. за единицу, то новым оптимальным сочетанием явится способ В, при котором используется большее количество капитала и Меньшее количество труда, а общая сумма издержек в этом случае составляет только 7 долл. Читателю следовало бы проверить это, подсчитав новые суммы издержек производства по всем другим сочетаниям, и убедиться в том, что все остальные методы производства обходятся дороже. (Рассчитайте и впишите в табл. 26-3 пропущенные данные об издержках производства.)
Точно такие же расчеты можно проделать по любым другим видам продукции; если цены на все факторы производства известны, то мы можем экспериментировать до тех пор, пока не найдем такое сочетание между различными факторами производства, при котором достигаются наименьшие издержки. (Для того чтобы закрепить ваши знания в данной области, решите вопрос об оптимальном сочетании факторов производства, обеспечивающем наименьшие издержки, когда цена на единицу труда составляет 2 долл. и цена единицы капитала — 3 долл.)
Кривые равного выпуска продукции и равных издержек. Графическое решение вопроса о наименьших издержках
Те повседневные арифметические расчеты, с помощью которых подбирается сочетание факторов, обеспечивающее для фирмы наименьшие издержки производства, можно сделать еще более наглядными, если использовать графики. Исходя из приведенных в таблице значений функции производства, мы можем графически изобразить различные сочетания факторов производства, которые обеспечат выпуск данного количества продукции. Рис. 128 представляет точное воспроизведение данных, приведенных в табл. 26-3, плавная линия кривой на графике показывает различные сочетания затрат труда и капитала, которые обеспечивают выпуск 346 единиц продукции. Эту линию можно назвать «кривой безразличия производства» по аналогии с кривой безразличия потребителя, о которой мы говорили в приложении к главе 21 Теория спроса и полезности. Но более точно можно было бы назвать ее кривой «равного продукта». (Вы должны суметь нанести на рис. 128 пунктирную кривую, соответствующую кривой равного продукта для выпуска в 490 единиц. Вам следует представить, что можно начертить бесчисленное множество такого рода кривых равного продукта, так же как на топографической или метеорологической карте можно нанести бесконечно большое число кривых одинаковых высот или равных барометрических давлений.)
Если даны цены на труд и капитал, фирма может рассчитать общую сумму издержек производства для точек А, В, С и D или для любой другой точки, находящейся на кривой равного продукта. Очевидно, что эти расчеты покажут максимум прибыли для фирмы только в том случае, когда на кривой равного продукта будет обнаружена точка оптимального сочетания факторов, при которой обеспечиваются наименьшие издержки производства.
Фирма может попытаться избавить себя от утомительных арифметических расчетов, используя более простой, чисто графический прием: один раз рассчитать и нанести на график общую сумму издержек производства для каждого возможного сочетания между собою факторов — капитала и труда. Это проделано при составлении графика на рис. 129, где семейство параллельных отрезков прямых линий представляет все возможные кривые равных издержек при цене труда в 2 долл. за единицу и цене капитала в 3 долл. за единицу (см. рис. 129).
В-третьих, линии равных издержек выражаются отрезками параллельных прямых:
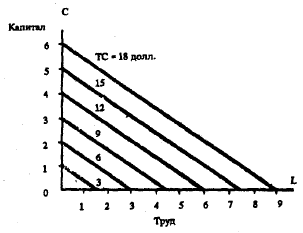
Рис. 129. Линии равных издержек. Каждая точка на данной линии выражает одну и ту же общую сумму издержек производства. Линии равных издержек являются прямыми потому, что цены на факторы производства сохраняют постоянные значения. Все эти линии имеют одинаковый угол наклона к оси абсцисс, численно равный отношению цены на рабочую силу к цене капитала, то есть 2 долл./3 долл., поэтому все они расположены параллельно друг другу.
Чтобы найти общую сумму издержек производства для любой точки, мы должны просто прочесть число, обозначающее проходящую через эту точку линию равных издержек. Все линии равных издержек изображены прямыми и параллельными, так как предполагается, что фирма может купить по постоянным ценам любое количество тех факторов производства, которые она пожелает приобрести. Угол наклона этих линий к оси абсцисс составляет несколько менее 45, так как цена единицы труда Pl несколько ниже цены единицы капитала Рс. Точнее говоря, мы всегда можем утверждать, что числовое значение угла наклона каждой линии равных издержек по отношению к оси абсцисс должно равняться отношению цены единицы труда к цене единицы капитала, то есть в данном случае должно составлять 2/3.
Внимательный читатель может заметить сходство между геометрическими построениями, описанными в этом разделе, и методами геометрического анализа потребительского равновесия, изложенными в приложении к главе 21. Каждая линия равных издержек показывает все возможности приобретения фирмой различных количеств труда и капитала при заранее данной общей величине издержек производства. Каждая линия является отрезком прямой, так как ее уравнение записано в виде ТС = 2 долл. х L + 3 долл. x С. Потребитель, о котором шла речь в приложении к главе 21, тоже покупает, только не услуги факторов производства, а товары. Другими словами, его «линия возможного потребительского спроса» расположена в точности параллельно линиям равных издержек, которые мы сейчас рассматриваем. Подобным образом мы можем объяснить также, почему в обоих случаях угол наклона линии рапных расходов к оси абсцисс выражает отношение между уровнями цен рассматриваемых товаров. Однако следует отметить и различия: мы предполагаем, что бюджет потребителя является величиной постоянной; отсюда для потребителя существовала только одна линия возможного потребительского спроса. Что касается фирмы, то она не ограничена какой-либо одной суммой издержек производства, следовательно, для того чтобы обнаружить условия равновесия, она должна проанализировать многочисленные линии равных издержек.
Теперь нетрудно обнаружить условия оптимального сочетания затрат различных факторов производства, — условия равновесия, при котором общая сумма издержек фирмы на производство данного количества продукции сводится к минимуму. На семейство линий равных издержек налагается одна кривая равного продукта. Это показано на рис. 130. Фирма всегда будет подбирать сумму издержек производства, двигаясь вдоль сильно вогнутой кривой на рис. 130, до тех пор, пока эта кривая не пересечет линию наиболее низких издержек производства. Равновесие поэтому будет достигаться не в точках А, В и D. Оно будет достигаться в точке С, еде кривая равного продукта касается (но не пересекает) той линии равных издержек, которая имеет наименьшую величину. Эта точка является и точкой касания, где угол наклона касательной к кривой равного продукта, конечно, в точности равен углу наклона линии равных издержек и кривые соприкасаются между собой только в одной точке.
В-четвертых, мы подвигаемся по кривой равного продукта к линии, характеризующей наименьшую общую сумму издержек:
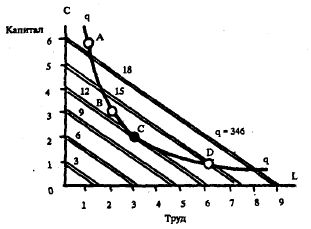
Рис. 130. Замещение факторов производства с целью обеспечения минимальных издержек производства. Точка, в которой кривая равного продукта касается (но не пересекает) линии, характеризующей наименьшую общую сумму издержек, выражает оптимальные условия обеспечения наименьших издержек. Соприкосновение с касательной означает, что отношения цен факторов производства пропорциональны соответствующим отношениям физических объемов предельного продукта (или «коэффициенты замещаемости» пропорциональны).
Мы уже знаем, что угол касательной к кривым равных издержек выражает отношение Pl : Рс. Но что же выражает угол наклона кривой равного продукта? Последний представляет своего рода «коэффициент замещаемости» для двух факторов производства. Этот «коэффициент замещаемости» зависит от относительной величины физических объемов предельного продукта двух факторов производства, точно так же, как и описанный ранее коэффициент замещаемости по двум товарам на кривой безразличия потребительских расходов, который равен отношению между предельными или добавочными полезностями двух товаров (см. приложение к главе 21 Графический анализ равновесия в потреблении).
Условия обеспечения наименьших издержек
Итак, наше равновесие, при котором достигаются наименьшие издержки, может быть определено любым из описанных ниже эквивалентных между собой соотношений.
1. Отношение физических объемов предельного продукта для любых двух факторов производства должно равняться отношению цен на эти факторы. Это можно выразить следующим образом: Koэффициент замещаемости, или отношение:
| Физический объем предельного продукта труда | = | Цена единицы труда |
| Физический объем предельного продукта капитала | Цена единицы капитала |
2. Физический объем предельного продукта в расчете на последний доллар издержек должен быть равным для каждого из факторов производства. Это можно выразить следующим образом:
| Физический объем предельного продукта труда | = | Физический объем предельного продукта капитала |
| Цена труда | Цена капитала |
Это условие сохраняет силу при любом количестве факторов производства. Содержание условия (2) подробно рассматривалось в основном тексте данной главы. (Оно могло бы быть выведено из условия (1) путем перестановки членов из числителя одной дроби в знаменатель другой дроби, то есть путем «коммутативного перемещения», которое всегда справедливо для алгебраических расчетов.)
Но исследователь не должен удовлетворяться любым абстрактным объяснением такого рода. Ему следует всегда помнить повседневный экономический смысл, содержащийся в этих соотношениях: данные соотношения показывают, как фирма перераспределяет свои затраты между различными факторами производства в том случае, если какой-либо фактор обещает принести более высокий доход в расчете на последний доллар, израсходованный на покупку этого фактора производства. Наконец, мы можем выразить указанные условия обеспечения наименьших издержек в следующей форме:
3. Цены на отдельные факторы производства должны быть пропорциональны соответствующим физическим объемам производимых с их помощью предельных продуктов, при атом коэффициентом пропорциональности будут предельные издержки производства. Почему каждый из этих физических объемов предельного продукта в расчете на 1 долл. издержек производства равен обратной величине предельных издержек, или 1/МС? Потому, что дополнительный выпуск продукции, приходящийся на 1 долл. издержек, представляет собой не что иное, как обратную величину дополнительных денежных затрат в долларах в расчете на единицу продукции, то есть величину, которую мы на протяжении всей книги называем предельными издержками, МС. Это можно выразить так:
Предельные издержки МС для выпускаемой продукции, умноженные на физический объем предельного продукта труда, равны цене единицы труда.
Предельные издержки МС для выпускаемой продукции, умноженные на физический объем предельного продукта капитала, равны цене единицы капитала.
И так далее для любого количества факторов производства.
Условия (1), (2) и (3) обеспечения наименьших издержек эквивалентны между собой. Каждое из них сохраняет силу для любой точки, расположенной на кривой общей суммы затрат, независимо от того, в каких размерах выпускается продукция. Они ничего не говорят фирме о том, в какой точке кривой она должна наконец приступить к производству.
Соотношения для дохода от предельного продукта, обеспечивающие получение наибольшей прибыли
Теперь, однако, мы дополнительно введем в анализ условие обеспечения наивысшей прибыли, которое выражается формулой MR = МС. При этом вспомним определение дохода от предельного продукта: он равен физическому объему предельного продукта, умноженному на предельный доход. Теперь мы можем сочетать между собой отношение (3), характеризующее условия достижения наименьших издержек с условием обеспечения наивысшей прибыли; благодаря этому нам удается получить окончательную формулу, характеризующую условия равновесия:
Доход от предельного продукта труда = Цене единицы труда.
Доход от предельного продукта капитала = Цене единицы капитала.
и так далее для любого числа факторов производства.
Таким образом, наш графический анализ привел нас в конечном счете к тому же выводу, к какому мы пришли в основном тексте данной главы Теория производства и предельных продуктов на основе обычных здравых рассуждений. Этот вывод заключается в том, что мы перестанем расширять использование определенного фактора производства только тогда, когда доход от предельного продукта, производимого с помощью этого фактора, снизится до уровня рыночной цены на единицу данного фактора. Именно это соотношение и лежит в основе кривой, характеризующей спрос фирмы на факторы производства.
