Ряды динамики
Понятие о рядах динамики
Одним из основных положений научной методологии является необходимость изучать все явления и процессы в развитии, во времени, т.е. в динамике. Для этого используется система статистических методов, основанных на построении рядов динамики.
Ряд динамики (хронологический ряд, динамический ряд, временной ряд) – это последовательность упорядоченных во времени числовых значений показателей, характеризующих уровень развития изучаемого явления.
Ряд динамики включает два обязательных элемента: время (t) и конкретное значение показателя, или уровень ряда (у).
Многообразие видов статистических показателей предопределяет возможность классифицировать ряды динамики на основании признаков, приведенных в таблице 9.1.
Таблица 9.1
| Классификационный признак | Название ряда динамики | Характеристика ряда динамики |
|---|---|---|
| По отношению показателя (уровня ряда) ко времени | Моментные | Последовательность уровней ряда, показывающих фактическое наличие изучаемого явления в конкретный момент времени. |
| Интервальные | Последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. | |
| По форме представления уровней | Ряды абсолютных, относительных и средних величин | |
| По расстоянию между датами или интервалами времени | Полные | Имеют место если даты регистрации или окончания периодов следуют друг за другом с равными интервалами (равноотстоящие ряды динамики). |
| Неполные | Имеют место, если принцип равных интервалов не соблюдается. | |
| По числу показателей | Изолированные | Имеют место, если ведется анализ во времени одного показателя. |
| Комплексные (многомерные) | Имеют место, если в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления. | |
Уровни интервальных рядов динамики абсолютных величин можно суммировать, так как сумма уровней интервального ряда дает вполне реальный показатель. Например, общая сумма доходов и расходов бюджета, общий выпуск продукции, общие затраты времени, общий объем продаж ценных бумаг и т.д. за обусловленный период.
Уровни моментного ряда суммированию не подлежат потому, что полученная сумма реального содержания, как правило, не имеет. В этом состоит важное аналитическое отличие интервальных рядов абсолютных величин от моментных.
При построении рядов динамики необходимо соблюдать определенные правила, приведенные на рис. 9.1.
1. Периодизация развития, т.е. ряд динамики должен быть расчленен во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития
2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методике расчета и т.д.
Сопоставимость данных по указанным параметрам означает то, что уровни показателя в каждый момент или интервал времени исчислены в единых территориальных границах, охватывают равное число объектов, рассчитаны по одной методике и в одинаковых единицах измерения, и т.д.
3. Величины временных интервалов рядов динамики должны соответствовать интенсивности изучаемых процессов
Чем больше вариация уровней во времени, тем чаще следует делать замеры значений показателей. Соответственно для стабильных процессов интервалы фиксации данных можно увеличить
4. Числовые уровни рядов динамики должны быть упорядоченными во времени
Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями
Рисунок 9.1 – Правила построения рядов динамики
Территориальная, количественная, методическая сопоставимость уровней ряда обеспечивается смыканием рядов динамики. Чтобы провести смыкание двух рядов динамики в один, необходимо, чтобы для переходного периода имелись уровни, исчисленные по разной методике, в разных границах и т.п. Недостающие уровни сопоставимого ряда получают путем пересчета несопоставимых уровней ряда в условные уровни, для чего подбирают методику исходя из особенностей показателей смыкаемых рядов.
Пример смыкания рядов динамики данных, отличающихся друг от друга по числу включаемых в исследуемую совокупность единиц
Данные, отражающие розничный товарооборот города N за 2013-2018 гг., приведены в таблице 9.2. Для анализа динамики розничного товарооборота города N за обусловленный период необходимо привести уровни хронологического ряда к сопоставимому виду, так как объемы продаж без мелкого опта и с мелким оптом количественно отличаются и не могут быть использованы для анализа.
Таблица 9.2
| Розничный товарооборот | 2013 г. | 2014 г. | 2015 г. | 2016 г. | 2017 г. | 2018 г. |
|---|---|---|---|---|---|---|
| Без мелкого опта | 277 | 281 | 292 | – | – | – |
| С мелким оптом | – | – | 347 | 416 | 474 | 498 |
Решение
Для приведения ряда динамики к сопоставимому виду определим для 2015 года коэффициент соотношения уровней двух рядов: 347 : 292 = 1,188. Умножая этот коэффициент на уровни ряда, отражающие розничный товарооборот, не учитывающий мелкий опт, получаем их значения, сопоставимые с уровнями ряда, показывающими данные продаж товара розничными продавцами, включающие объемы реализации мелкими оптовыми партиями. Так, для 2013 года объем розничного товарооборота, включающего мелкий опт, равен 277 × 1,188 = 329 млн. руб., а для 2014 года – 281 × 1,188 = 334 млн. руб. (рассчитанные значения – условные данные). Полученный сопоставимый ряд динамики розничного товарооборота города N приведен в таблице 9.3.
Таблица 9.3
| Годы | 2013 г. | 2014 г. | 2015 г. | 2016 г. | 2017 г. | 2018 г. |
|---|---|---|---|---|---|---|
| Розничный товарооборот (с мелким оптом), млн. руб. | 329 | 334 | 347 | 416 | 474 | 498 |
Пример смыкания рядов динамики данных, отличающихся друг от друга методикой расчета показателей
В таблице 9.4 приведены данные, отражающие стоимость основных производственных фондов (ОПФ) предприятий отрасли на начало 2013-2018 гг. и их среднегодовую стоимость за соответствующие годы. Необходимо провести смыкание рядов динамики, данные которых, исчислены по разным методикам и, следовательно, не сопоставимы.
Таблица 9.4
| Стоимость ОПФ | 2013 г. | 2014 г. | 2015 г. | 2016 г. | 2017 г. | 2018 г. |
|---|---|---|---|---|---|---|
| На начало года | 1,2 | 1,4 | 1,8 | 1,6 | – | – |
| Среднегодовая | – | – | – | 1,8 | 2,1 | 2 |
Решение
Между показателями таблицы 9.4 существует функциональная зависимость: среднегодовая стоимость основных производственных фондов рассчитывается по формуле 4.21 как сумма стоимостей основных производственных фондов на начало и конец года, деленная пополам. Отметим, что стоимость основных производственных фондов на конец одного периода соответствует стоимости ОПФ на начало следующего за ним периода.
Данные таблицы 9.4 позволяют привести каждый из представленных рядов в сопоставимый вид по методике исчисления показателей, сомкнув их следующим образом.
Так, зная стоимость основных производственных фондов на начало и конец года, получаем их среднегодовую стоимость в 2013 г.: ОПФ2013 = 1,3 млрд. руб.; в 2014 г. – ОПФ2014 = 1,6 млрд. руб.; в 2015 г. – 1,7 млрд. руб.
Для того чтобы определить стоимость основных производственных фондов на начало 2017 г. и 2018 г. найдем соответственно стоимость основных производственных фондов на конец 2011 г. и 2012 г., предварительно преобразовав формулу расчета среднегодовой стоимости ОПФ.
По результатам расчетов проведем смыкание рядов динамики стоимости основных производственных фондов на начало 2013-2018 гг. и среднегодовой стоимости основных производственных фондов в исследуемом периоде, построив два самостоятельных ряда с сопоставимыми данными, представленных в таблице 9.5.
Таблица 9.5
| Стоимость ОПФ | 2013 г. | 2014 г. | 2015 г. | 2016 г. | 2017 г. | 2018 г. |
|---|---|---|---|---|---|---|
| На начало года | 1,2 | 1,4 | 1,8 | 1,6 | 2,0 | 2,2 |
| Среднегодовая | 1,3 | 1,6 | 1,7 | 1,8 | 2,1 | 2 |
Статистические характеристики рядов динамики
При изучении развития явления во времени оценивается интенсивность развития и рассчитываются средние показатели динамики, соответствующие определенным интервалам (моментам) исследуемого периода.
Для характеристики интенсивности изменения явления во времени рассчитываются показатели абсолютного прироста, коэффициента роста, темпа роста, темпа прироста, абсолютного значения одного процента прироста, методики расчета которых приведены в таблице 9.6. В основе расчета этих показателей лежит сравнение определенных уровней ряда с уровнями, принятыми за базу сравнения.
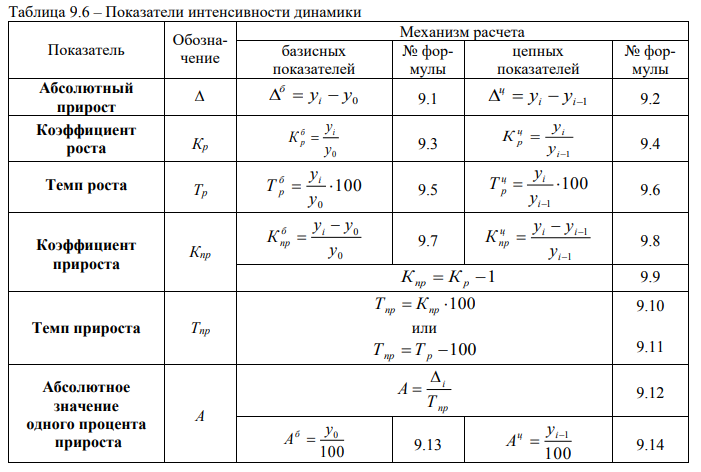
Уровни показателей, соответствующие определенному i-ому периоду (моменту) времени, обозначаются уi; уровни показателей, соответствующие периоду (моменту) времени, предшествующему i-ому периоду (моменту) времени, – уi-1; уровни показателей, соответствующие периоду (моменту) времени, начальному в ряду динамики, – у0.
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели динамики, характеризующие окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень до конкретного i-го периода.
Если же сравнение проводится с предыдущим периодом или моментом времени, то получают цепные показатели динамики, характеризующие интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
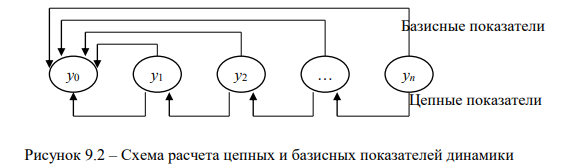
Схематично механизм расчета базисных и цепных показателей динамики показан на рис. 9.2.
Абсолютный прирост показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
Коэффициент роста показывает, во сколько раз данный уровень превышает уровень, принятый за базу сравнения.
Темп роста показывает, сколько процентов составляет данный уровень по сравнению с уровнем принятым за базу сравнения.
Темп прироста показывает, на сколько процентов определенный уровень ряда больше (меньше) уровня, принятого за базу сравнения.
Базисный абсолютный прирост равен сумме цепных абсолютных приростов в исследуемом периоде, а базисный коэффициент роста равен произведению цепных коэффициентов роста в исследуемом периоде.
Зависимость между базисными и цепными показателями динамики характеризуется формулами:

и

Макет таблицы, в которой приводятся результаты расчетов показателей интенсивности динамики соответствующего социально-экономического явления (показателя), представлен с помощью таблицы 9.7
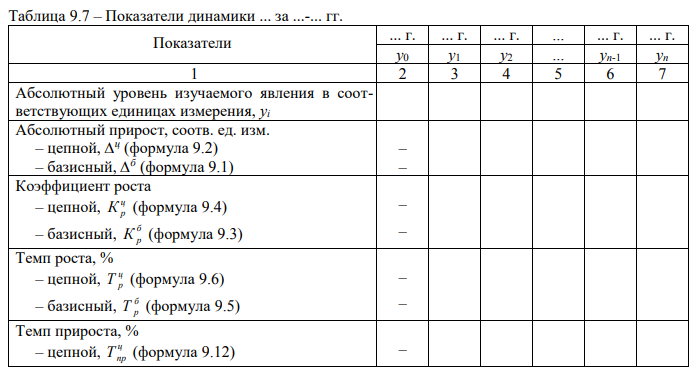
Наряду с показателями интенсивности динамики, для характеристики ряда динамики используют систему средних показателей динамики: средний уровень ряда; средний абсолютный прирост; средний темп роста; средний темп прироста, методики расчета которых приведены в таблице 9.8.
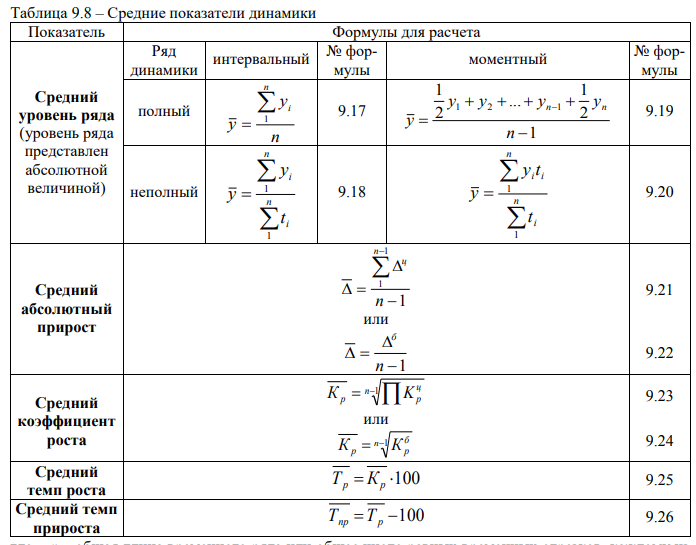
Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал (момент) из имеющейся временной последовательности.
Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.
Пример расчета среднего уровня неполного интервального ряда динамики
В таблице 9.9 приведены данные, характеризующие объем реализации новогодних и рождественских подарков в магазинах и других торговых точках города N в декабре прошедшего года.
Необходимо определить среднесуточный объем продаж новогодних и рождественских подарков в городе N в декабре прошедшего года.
Таблица 9.9
| Период | 01.12-10.12 | 11.12-17.12 | 18.12-27.12 | 28.12-31.12 |
| Количество дней в периоде | 10 | 7 | 10 | 4 |
| Объем продаж новогодних и рождественских подарков, млн. руб. | 0,2 | 0,5 | 1,6 | 1,4 |
Решение
По формуле 9.18 средний уровень продаж новогодних и рождественских подарков в день в декабре прошедшего года составил: 0,12 млн. руб.
Пример расчета среднего уровня полного моментного ряда динамики
По данным о стоимости основных производственных фондов предприятий отрасли на начало 2013-2018 гг. (см. табл. 9.5) необходимо определить их среднегодовую стоимость за период 2013-2017 гг.
Решение
По формуле 9.19 среднегодовая стоимость основных производственных фондов предприятий отрасли в исследуемом периоде (с 2013 г. по 2017 г. включительно) равна: 1,7 млрд. руб.
Пример расчета среднего уровня неполного моментного ряда динамики
По данным таблицы 9.10 необходимо рассчитать среднюю численность работников предприятия в феврале текущего года.
Таблица 9.10
| Дни февраля | 01-05 | 06-08 | 09-12 | 13-19 | 20-21 | 22-26 | 27-28 |
| Число дней, в течение которых списочный состав работников не менялся | 5 | 3 | 4 | 7 | 2 | 5 | 2 |
| Состояло в списках предприятия, чел. | 128 | 130 | 129 | 130 | 131 | 130 | 132 |
Решение
По формуле 9.20 среднедневная численность работников предприятия в феврале составила 129,7 чел.
Сравнительный анализ взаимосвязанных рядов динамики
Для оценки интенсивности изменения уровней показателей взаимосвязанных рядов динамики проводят их сравнительный анализ.
Под взаимосвязанными рядами динамики понимают такие, в которых уровни одного ряда в какой-то степени определяют уровни другого. Например: ряд, отражающий внесение удобрений на 1 га, связан с временным рядом урожайности; ряд средней выработки связан с рядом динамики заработной платы работников и т. д.
В простейших случаях для характеристики взаимосвязи двух и более рядов их приводят к общему основанию, для чего берут в качестве базисных уровни за один и тот же период, как правило, начальный в ряду динамики, и исчисляют коэффициенты опережения по темпам роста или прироста.
Коэффициенты опережения по темпам роста представляют собой отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда и рассчитываются по формуле:

Аналогично находятся и коэффициенты опережения по темпам прироста.
Пример сравнительного анализа взаимосвязанных рядов динамики
По данным таблицы 9.11 необходимо провести сравнительный анализ рядов динамики среднемесячной номинальной начисленной заработной платы работников по полному кругу организаций в целом по экономике Российской Федерации (ЗПРФ) и в сфере рыболовства и рыболовства (ЗПрр) в 2000-2018 гг.
Взаимосвязанный характер представленных рядов динамики обусловлен тем, что общий уровень заработной платы в целом по стране представляет собой среднюю величину оплаты труда работников по видам экономической деятельности.
Таблица 9.11
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
|---|---|---|---|---|---|---|---|---|---|---|
| Экономика в целом | 2223 | 3240 | 4360 | 5499 | 6740 | 8555 | 10634 | 13593 | 17290 | 18638 |
| Рыболовство, рыбоводство | 2846 | 3839 | 5031 | 5445 | 7085 | 10234 | 12311 | 14797 | 19499 | 22914 |
| Годы | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|
| Экономика в целом | 20952 | 23369 | 26629 | 29792 | 32495 | 34030 | 36709 | 39167 | 43724 |
| Рыболовство, рыбоводство | 23782 | 25940 | 29201 | 32437 | 37062 | 46676 | 54927 | 68032 | 75766 |
Решение
Для сравнительного анализа рядов динамики среднемесячной номинальной начисленной заработной платы работников по полному кругу организаций в целом по экономике Российской Федерации и в сфере рыболовства и рыболовства в 2000-2018 гг. по формуле 9.27 рассчитаем соответствующие коэффициенты опережения по темпам роста. Результаты расчетов сведены в таблицу 9.12.
Таблица 9.12
| Годы | Показатели, руб. | Цепные темпы роста (Тцр), % | Kопер.поТцр | Базисные темпы роста (Тбр), % | Kопер.поТбр | |||
|---|---|---|---|---|---|---|---|---|
| ЗПРФ | ЗПрр | ЗПРФ | ЗПрр | ЗПРФ | ЗПрр | |||
| 2000 | 2223 | 2846 | – | – | – | – | – | – |
| 2001 | 3240 | 3839 | 145,7 | 134,9 | 0,926 | 145,7 | 134,9 | 0,926 |
| 2002 | 4360 | 5031 | 134,6 | 131,0 | 0,973 | 196,1 | 176,8 | 0,902 |
| 2003 | 5499 | 5445 | 126,1 | 108,2 | 0,858 | 247,4 | 191,3 | 0,773 |
| 2004 | 6740 | 7085 | 122,6 | 130,1 | 1,061 | 303,2 | 248,9 | 0,821 |
| 2005 | 8555 | 10234 | 126,9 | 144,4 | 1,138 | 384,8 | 359,6 | 0,935 |
| 2006 | 10634 | 12311 | 124,3 | 120,3 | 0,968 | 478,4 | 432,6 | 0,904 |
| 2007 | 13593 | 14797 | 127,8 | 120,2 | 0,941 | 611,5 | 519,9 | 0,850 |
| 2008 | 17290 | 19499 | 127,2 | 131,8 | 1,036 | 777,8 | 685,1 | 0,881 |
| 2009 | 18638 | 22914 | 107,8 | 117,5 | 1,090 | 838,4 | 805,1 | 0,960 |
| 2010 | 20952 | 23782 | 112,4 | 103,8 | 0,923 | 942,5 | 835,6 | 0,887 |
| 2011 | 23369 | 25940 | 111,5 | 109,1 | 0,978 | 1051,2 | 911,5 | 0,867 |
| 2012 | 26629 | 29201 | 114,0 | 112,6 | 0,988 | 1197,9 | 1026,0 | 0,856 |
| 2013 | 29792 | 32437 | 111,9 | 111,1 | 0,993 | 1340,2 | 1139,7 | 0,850 |
| 2014 | 32495 | 37062 | 109,1 | 114,3 | 1,048 | 1461,8 | 1302,2 | 0,891 |
| 2015 | 34030 | 46676 | 104,7 | 125,9 | 1,202 | 1530,8 | 1640,1 | 1,071 |
| 2016 | 36709 | 54927 | 107,9 | 117,7 | 1,091 | 1651,3 | 1930,0 | 1,169 |
| 2017 | 39167 | 68032 | 106,7 | 123,9 | 1,161 | 1761,9 | 2390,4 | 1,357 |
| 2018 | 43724 | 75766 | 111,6 | 111,4 | 0,998 | 1966,9 | 2662,2 | 1,354 |
Данные таблицы 9.12 показывают, что от года к году на протяжении 2000-2018 гг. среднемесячная номинальная начисленная заработная плата работников по полному кругу организаций в целом по экономике Российской Федерации росла опережающими темпами по сравнению с ростом среднемесячной номинальной начисленной заработной платы в рыболовстве и рыбоводстве в десяти случаях из восемнадцати, притом, что абсолютный уровень заработной платы в рыбоводстве и рыболовстве в 2018 году по сравнению с 2000 годом вырос в 27,6 раз, тогда как по стране в целом – в 19,7 раз. Опережение базисными темпами роста среднемесячной заработной платы в рыбохозяйственном секторе базисные темпы роста среднемесячной заработной платы по экономике страны в целом началось с 2015 года и продолжалось до конца анализируемого периода.
