Методические подходы к измерению взаимосвязей
Понятие о статистических связях
Все явления общественной жизни существуют не изолированно, они органично связаны между собой, зависят друг от друга, обусловливают одно другое и находятся в постоянном движении и развитии. Раскрывая взаимосвязи и взаимозависимости между явлениями, можно познать их суть и законы развития.
Причинная зависимость является основной формой закономерных связей, действующих в определенных условиях места и времени. Поэтому, для появления следствия необходимы и причины, и условия, т.е. соответствующие факторы.
Общественные явления или отдельные их признаки, оказывающие влияние на другие явления или свойства и определяющие их изменения, называются факторными, а общественные явления или отдельные их признаки, которые изменяются под влиянием соответствующих факторов, называются результативными.
По характеру зависимости явлений различают функциональные (жестко детерминированные) и статистические (или стохастически детерминированные) связи.
Функциональной называется связь, при которой определенному значению факторного признака всегда соответствует, как правило, одно значение результативного признака. Функциональные связи характеризуются полным соответствием между причиной и следствием. Вследствие этого функциональная зависимость всегда выражается точною математической формулой. При этом не обязательно, чтобы одному результативному признаку строго соответствовал только один факторный признак, как, например, в случае связи между длиной окружности и радиусом описываемой формулой: l = 2πR. Существуют функциональные связи, при которых результативный признак является функцией нескольких факторных признаков. Например, площадь земельного участка будет зависеть от длин его сторон: S = a×b. Функциональные зависимости изучаются точными науками, такими как математика, физика, химия и др. Они очень редко используются для исследования общественных явлений.
Статистическая связь не имеет ограничений и условий, присущих функциональной связи.
Связь является статистической, если с изменением значения факторного признака результативный признак может в определенных пределах принимать любые значения с некоторыми вероятностями, но его среднее значение или иные статистические характеристики (показатели вариации, асимметрии, эксцесса и т. п.) изменяются по определенному закону.
Важнейшим частным случаем статистической связи является корреляционная связь.
Слово «корреляция» (от английского correlation) означает соотношение, соответствие. Оно удачно отражает особенность зависимости, при которой определенному значению одного факторного признака может соответствовать несколько значений результативного признака, на основе которых можно определить среднюю величину результативного признака, соответствующую каждому конкретному значению факторного признака.
Связь, при которой разным значениям факторного признака соответствуют различные средние значения результативного признака, называется корреляционной связью. Именно корреляционные зависимости наиболее часто используются при исследовании общественных явлений.
Суть корреляционной зависимости сводится к тому, что, с изменением значения факторного признака х закономерным образом изменяется среднее значение результативного признака у, в то время как в каждом отдельном случае значение результативного признака у (с различными вероятностями) может принимать множество различных значений.
Корреляционная связь между признаками может возникать разными путями:
– во-первых, как причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, зависимость заработной платой работников от стажа их работы, себестоимости продукции от объемов производства продукции, урожайности зерновых от внесения удобрений и т.п.;
– во-вторых, как связь между двумя следствиями общей причины. Классический пример такого рода корреляционной связи приведен А. Чупровым, крупнейшим российским статистиком ХХ века определившим, что прямая зависимость между убытками от пожара и числом пожарных команд в городе обусловлена общей причиной их величины – размером города;
– в-третьих, как взаимосвязь признаков, каждый из которых и причина, и следствие. Такова, например, корреляция между уровнями производительности труда рабочих и уровнем оплаты одного часа труда (часовой тарифной ставкой).
Характеристика основных разновидностей корреляционных связей представлена в таблице 7.1.
Таблица 7.1
| Классификационный признак | Название корреляции | Характеристика корреляционной связи |
|---|---|---|
| По направлению связи | Прямая | С ростом факторного признака растет и результативный признак. Например, с ростом производительности труда растет объем выпущенной продукции при прочих равных условиях |
| Обратная | С увеличением факторного признака результативный признак уменьшается или наоборот. Например, рост производительности труда приводит к снижению себестоимости единицы продукции при прочих равных условиях | |
| В соответствии с аналитическим выражением (по формуле) | Прямолинейная | Равным изменениям значений факторного признака соответствуют приблизительно равные изменения средних значений результативного признака |
| Криволинейная | Равным изменениям значений факторного признака соответствуют неравные изменения средних значений результативного признака | |
| По числу факторных показателей, учитываемых для оценки степени их влияния на результативный показатель | Парная | Связь между двумя показателями, один из которых является факторным, а другой – результативным |
| Множественная | Связь, возникающая от взаимодействия нескольких факторов с результативным показателем. Например, на урожайность зерновых культур влияют качество семян, количество внесенных удобрений, степень механизации сельхозпроизводства и др. В свою очередь, урожайность зерновых культур, количество внесенных удобрений, производительность труда и т.п. влияют на уровень себестоимости 1 ц зерновых культур |
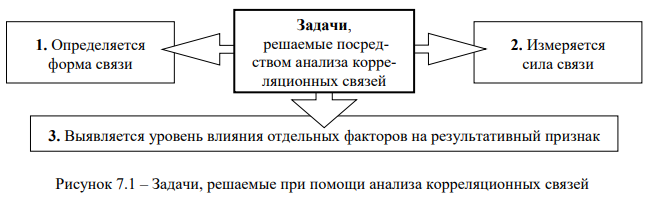
Задачи, решаемые при помощи анализа корреляционных связей, приведены на рис. 7.1.
Так как факторные и результативные признаки могут быть количественными и описательными (атрибутивными), т.е. не имеющими численного выражения, то выделяют параметрические и непараметрические методы измерения связей и соответствующие им параметрические и непараметрические показатели связи.
К параметрическим методам измерения связей относятся, например, методы аналитической группировки и корреляционно-регрессионного анализа, а к непараметрическим методам – методы сравнения параллельных рядов и измерения связи между атрибутивными признаками.
Метод сравнения параллельных рядов
Суть метода сравнения параллельных рядов состоит в том, что полученные в результате группировки и счетной обработки материалы статистического наблюдения располагаются ранжированными по факторному признаку параллельными рядами. Параллельно записываются значения результативного признака. Это дает возможность, сравнивая значения факторных и результативных показателей, проследить их соотношение, выявить наличие связи и ее направление.
Пример параллельных рядов, позволяющих оценить характер зависимости между стоимостью основных производственных фондов предприятия (факторным признаком) и объемом его товарной продукции (результативным признаком), приведен в таблице 7.2.
Таблица 7.2
| Показатели | Номер предприятия | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Стоимость основных производственных фондов (х), млрд. руб. | 5,3 | 6,4 | 7,9 | 8,3 | 9,2 | 10,1 | 12,5 | 13,0 | 14,6 | 15,7 |
| Товарная продукция (у), млрд. руб. | 5,8 | 7,6 | 8,7 | 9,1 | 11,9 | 12,3 | 13,8 | 14,0 | 15,2 | 17,6 |
Из данных таблицы 7.2 видно, что с увеличением стоимости основных производственных фондов выпуск продукции увеличивается.
Направление и силу корреляционной связи по данным параллельных рядов рассчитывают при помощи коэффициентов корреляции знаков (коэффициента Фехнера) и корреляции рангов (коэффициента корреляции рангов Спирмена).
Коэффициент Фехнера, предложенный немецким психологом Г.Т. Фехнером еще в XIX в., оценивает силу связи на основе сравнения знаков отклонений значений вариант от их среднего значения по каждому признаку. Совпадение знаков по факторному и результативному признакам означает согласованную вариацию, несовпадение – нарушение согласованности между признаками.
Коэффициент Фехнера (КФ), представляющий собой коэффициент корреляции знаков, рассчитывается по формуле:

где ΣС – сумма знаков, которые совпали в обоих рядах; ΣН – сумма не совпавших знаков.
Коэффициент Фехнера изменяется в пределах от -1 до +1. При приближении этого коэффициента к +1 наблюдается прямая и сильная согласованность между исследуемыми признаками, к – 1 имеет место сильная, однако обратная согласованность. При нуле согласованность между исследуемыми признаками отсутствует.
Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента Фехнера
По данным таблицы 7.2 необходимо оценить направление и силу связи между стоимостью основных производственных фондов и товарной продукцией предприятий одной отрасли с помощью коэффициента Фехнера.
Решение
По формуле 4.21 средняя стоимость основных производственных фондов предприятий отрасли равна: x = 10,3 млрд. руб.
По формуле 4.21 средний объем товарной продукции на одно предприятие отрасли равно: y = 11,6 млрд. руб.
Знаки отклонений от средней величины по признакам х и у приведены в таблице 7.3. Знак «минус» означает, что значение признака меньше средней величины, знак «плюс» – больше.
Таблица 7.3
| Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Знак отклонения от средней величины | x-x | - | - | - | - | - | - | + | + | + | + |
| y-y | - | - | - | - | + | + | + | + | + | + | |
| С или Н | С | С | С | С | Н | Н | С | С | С | С | |
Итак, в восьми случаях знаки совпали, в двух – не совпали, т.е. ΣС = 8, ΣН = 2.
По формуле 7.1 коэффициент Фехнера: 0,6, т.е. наблюдается достаточно сильная прямая связь между стоимостью основных производственных фондов предприятий и выпуском их продукции, предназначенной для реализации.
Более точно оценивает силу связи коэффициент корреляции рангов.
Ранги – это порядковые номера единиц совокупности в ранжированном ряду. Коэффициент корреляции рангов учитывает согласованность рангов, соответствующих отдельным единицам совокупности по каждому из двух исследуемых признаков.
Совокупность ранжируется по факторному признаку в порядке возрастания и единицам совокупности присваиваются соответствующие ранги. Параллельно проставляются ранги тех же единиц совокупности, какие они заняли бы в ранжированном ряду по результативному признаку.
Коэффициент корреляции рангов (ρ), предложенный американским ученым К. Спирменом, рассчитывается по формуле:

где d2 – квадрат разницы между величинами рангов в сравниваемых рядах; n – число рангов.
Коэффициент ранговой корреляции может принимать значения в пределах: -1 ≤ ρ ≤ 1. Когда ранги факторного признака полностью совпадают с рангами результативного признака, тогда имеет место почти прямая связь между признаками и ρ = 1. Если ранги расположились строго в противоположном направлении, то наблюдается полная обратная корреляция рангов и ρ = -1. При ρ = 0 корреляция рангов отсутствует.
Необходимо иметь в виду, что этот эмпирический показатель менее точен по сравнению с линейным коэффициентом корреляции и эмпирическим корреляционным отношением, а поэтому, когда он принимает крайние значения ±1 или 0, то это не означает, что существует функциональная связь или зависимость абсолютно отсутствует. Во всех других случаях, когда коэффициент ранговой корреляции не принимает крайних значений, он интерпретируется так же, как и коэффициент линейной корреляции и обладает такими же особенностями (п. 8.2, с. 131).
Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена
По данным таблицы 7.4 необходимо определить направление и силу связи между стоимостью основных производственных фондов (ОПФ) и выработкой продукции на одного рабочего по десяти предприятиям отрасли при помощи коэффициента корреляции рангов Спирмена.
Таблица 7.4
| Показатели | Номер предприятия | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Стоимость ОПФ (х), тыс. руб. | 26540 | 27800 | 23480 | 32400 | 28910 | 39150 | 31250 | 40000 | 41370 | 51990 |
| Выработка продукции (у), тыс. руб./чел. | 320 | 410 | 200 | 240 | 430 | 370 | 180 | 390 | 440 | 450 |
Решение
В таблице 7.5 проранжируем предприятия отрасли по стоимости основных производственных фондов (факторному признаку) в порядке возрастания и присвоим им соответствующие ранги. Параллельно проставим ранги тех же предприятий, какие они заняли бы в ранжированном ряду по выработке продукции на одного рабочего (результативному признаку). Вспомогательные данные для расчета коэффициента корреляции рангов Спирмена также приведены в таблице 7.5.
Таблица 7.5
| № по порядку | Стоимость ОПФ (х), тыс. руб. | Выработка продукции (у), тыс. руб./чел | Ранги предприятий (R) по признакам х и у | Разность рангов d = Rх - Rу |
d2 | |
|---|---|---|---|---|---|---|
| Rх | Rу | |||||
| 1 | 23480 | 200 | 1 | 2 | -1 | 1 |
| 2 | 26540 | 320 | 2 | 4 | -2 | 4 |
| 3 | 27800 | 410 | 3 | 7 | -4 | 16 |
| 4 | 28910 | 430 | 4 | 8 | -4 | 16 |
| 5 | 31250 | 180 | 5 | 1 | 4 | 16 |
| 6 | 32400 | 240 | 6 | 3 | 3 | 9 |
| 7 | 39150 | 370 | 7 | 5 | 2 | 4 |
| 8 | 40000 | 390 | 8 | 6 | 2 | 4 |
| 9 | 41370 | 440 | 9 | 9 | 0 | 0 |
| 10 | 51990 | 450 | 10 | 10 | 0 | 0 |
| Всего | х | х | х | х | х | 70 |
По формуле 7.2 коэффициент корреляции рангов Спирмена = 0,576, что указывает на заметную прямую связь между стоимостью основных производственных фондов предприятий отрасли и выработкой продукции на одного рабочего.
Существует правило, касающееся повторяющихся вариант, ранг которых определяется как средняя арифметическая соответствующих рангов, например, ранг одинаковых величин, занимающих 4 и 5 место, равен 4,5 («четыре целых пять десятых»). Соответственно одинаковым по порядку четвертому и пятому значениям признака будут присвоены одинаковые ранги 4,5.
В таком случае коэффициент корреляции рангов Спирмена вычисляется по формуле:
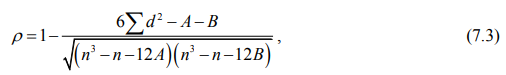
где А и В рассчитываются соответственно по формулам:

j – номера связок (совпадений значений) по порядку для признака х;
Аj – число одинаковых рангов в j-й связке по х;
k – номера связок (совпадений значений) по порядку для признака у;
Вk – число одинаковых рангов в k-й связке по у.
Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена в случае совпадения их значений
По данным таблицы 7.6 необходимо определить направление и силу связи между численностью работников 10 предприятий одного региона и величиной их основных производственных фондов (ОПФ).
Таблица 7.6
| Показатели | Номер предприятия | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Среднесписочная численность персонала, чел. | 90 | 350 | 1000 | 350 | 200 | 350 | 28 | 90 | 2500 | 850 |
| Среднегодовая стоимость ОПФ, млрд. руб. | 0,24 | 2,98 | 5,65 | 1,26 | 1,20 | 1,20 | 0,50 | 2,15 | 80,50 | 5,65 |
Решение
В таблице 7.7 проранжируем предприятия региона по стоимости основных производственных фондов (факторному признаку, так как численность работников предприятия зависит от количества эксплуатируемого на предприятии оборудования и других объектов основных фондов) в порядке возрастания и присвоим им соответствующие ранги. Параллельно проставим ранги тех же предприятий, какие они заняли бы в ранжированном ряду по среднесписочной численности работников (результативному признаку). Вспомогательные данные для расчета коэффициента корреляции рангов Спирмена также приведены в таблице 7.7.
Таблица 7.7
| № по порядку | Среднегодовая стоимость ОПФ (х), млрд. руб. | Среднесписочная численность персонала (у), чел. | Ранги предприятий (R) по признакам х и у | Разность рангов d = Rх - Rу | d2 | |
|---|---|---|---|---|---|---|
| Rх | Rу | |||||
| 1 | 0,24 | 90 | 1 | 2,5 | -1,5 | 2,25 |
| 2 | 0,5 | 28 | 2 | 1 | 1 | 1 |
| 3 | 1,2 | 200 | 3,5 | 4 | -0,5 | 0,25 |
| 4 | 1,2 | 350 | 3,5 | 6 | -2,5 | 6,25 |
| 5 | 1,26 | 350 | 5 | 6 | -1 | 1 |
| 6 | 2,15 | 90 | 6 | 2,5 | 3,5 | 12,25 |
| 7 | 2,98 | 350 | 7 | 6 | 1 | 1 |
| 8 | 5,65 | 850 | 8,5 | 8 | 0,5 | 0,25 |
| 9 | 5,65 | 1000 | 8,5 | 9 | -0,5 | 0,25 |
| 10 | 80,5 | 2500 | 10 | 10 | 0 | 0 |
| Всего | х | х | х | х | х | 24,5 |
В ранжированном ряду по факторному признаку повторяются варианты, стоящие на 3 и 4 месте и на 8 и 9 месте, следовательно, ранги этих вариант соответственно будут равны 3,5 ((3+4):2) и 8,5 ((8+9):2).
В ранжированном ряду по результативному признаку повторяются варианты, стоящие на 2 и 3 месте и на 5, 6 и 7 месте, следовательно, ранги этих вариант соответственно будут равны 2,5 ((2+3):2) и 6 ((5+6+7):3).
По формуле 7.4: A = 1.
По формуле 7.5: B = 2,5.
По формуле 7.3 коэффициент корреляции рангов Спирмена равен: 0,852.
Полученное значение коэффициента корреляции рангов Спирмена свидетельствует о тесной прямой зависимости между величиной основных производственных фондов и численностью работников предприятия.
Метод аналитической группировки. Таблицы взаимной сопряженности
Наличие зависимости между показателями, характеризующими статистическую совокупность, можно выявить с помощью аналитической группировки. Напомним, что статистические группировки, при помощи которых выявляют взаимосвязи между признаками общественных явлений, называются аналитическими.
Метод аналитических группировок как способ выявления корреляционной зависимости между показателями относится к числу наиболее важных методов исследования взаимосвязей.
Результаты группировки единиц совокупности оформляются в виде таблицы, в которой приводится комбинационное распределение единиц совокупности по двум признакам. Такие таблицы называют таблицами взаимной сопряженности. Примером таблицы взаимной сопряженности можно рассматривать таблицу 5.11, в которой приведена группировка сельскохозяйственных предприятий с разной урожайностью зерновых культур по организационно-правовой форме.
Если в таблице оба признака, по которым дано распределение единиц совокупности, количественные, то такая таблица взаимной сопряженности называется корреляционной.
Корреляционная таблица строится по типу «шахматной», т.е. в подлежащем таблицы выделяются группы по факторному признаку х, в сказуемом – по результативному у или наоборот, а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у.
Для выявления зависимости между непрерывными количественными признаками в сформированных группах по факторному и результативному признакам в качестве х и у принимаются середины соответствующих интервалов.
Макет корреляционной таблицы показан с помощью таблицы 7.8.
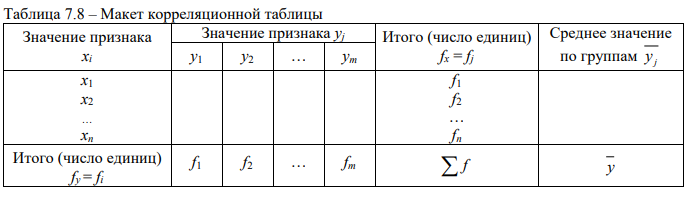
Корреляционная связь существует, если по мере увеличения значения х групповые средние значений у (yj) тоже увеличиваются (или уменьшаются) от группы к группе. Таким образом, сравнивая изменения средних значений результативного признака с изменением средних значений факторного признака, выявляют характер связи между ними.
О наличии и направлении связи можно судить и по «внешнему виду» таблицы, т.е. по расположению в ней частот.
Так, если числа (частоты) расположены (разбросаны) в клетках таблицы беспорядочно, то это чаще всего свидетельствует либо об отсутствии связи между группировочными признаками, либо об их незначительной зависимости. Если же частоты сконцентрированы ближе к одной из диагоналей и центру таблицы, образуя своего рода эллипс, то это почти всегда свидетельствует о наличии зависимости между х и у, близкой к линейной. Диагональ из верхнего левого угла в нижний правый свидетельствует о прямой линейной зависимости между показателями х и у, а из нижнего левого угла в верхний правый – об обратной.
Наглядно проиллюстрировать наличие и форму зависимости между показателями х и у по данным корреляционной таблицы можно и графически.
При построении эмпирической линии регрессии по данным корреляционной таблицы на графике по оси абсцисс отражают значения факторного признака (или середины соответствующих интервалов) х, а по оси ординат – групповые средние результативного показателя, т.е. yj. Для большей наглядности на графике по исходным данным можно построить «корреляционное поле», а затем на его фоне – эмпирическую линию регрессии.
Корреляционное поле представляет, по существу, ту же корреляционную таблицу, в клетках которой вместо чисел проставлено соответствующее число точек. Корреляционное поле отражает не только общую зависимость между х и у, но и концентрацию индивидуальных точек вокруг линии регрессии показателя yj.
На рис. 7.2 показаны варианты распределения корреляционного поля.
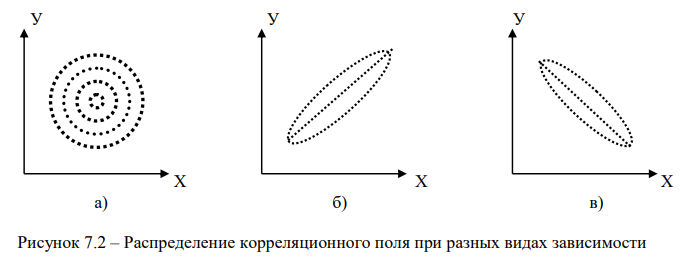
Если точки расположены хаотично по всему полю, то это свидетельствует об отсутствии зависимости между двумя признаками (рис. 7.2, а); если они сконцентрированы около оси, идущей от нижнего левого угла к верхнему правому (рис. 7.2, б), – это прямая зависимость между исследуемыми признаками; если точки будут сконцентрированы около оси, пролегающей от верхнего левого угла к нижнему правому (рис. 7.2, в) – имеет место обратная зависимость.
Пример корреляционной таблицы, в которой приведено распределение работников предприятия по уровню квалификации, характеризующегося их тарифным разрядом, и уровню месячной заработной платы, показан с помощью данных таблицы 7.9.
Таблица 7.9
| Разряд работников (xi) | Месячная заработная плата, руб. (yj) | Итого (fx = fj) | Среднемесячный заработок по группам, руб. (yj) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 6000- 8000 | 8000- 10000 | 10000- 12000 | 12000- 14000 | 14000- 16000 | 16000- 18000 | 18000- 20000 | |||
| 7000 | 9000 | 11000 | 13000 | 15000 | 17000 | 19000 | |||
| I | 3 | 8 | 1 | – | – | – | – | 12 | 8667 |
| II | 2 | 6 | 14 | 3 | – | – | – | 25 | 10440 |
| III | – | 1 | 4 | 20 | 5 | – | – | 30 | 12930 |
| IV | – | – | 1 | 6 | 9 | 4 | – | 20 | 14600 |
| V | – | – | – | 1 | 1 | 5 | 3 | 10 | 17000 |
| VI | – | – | – | – | – | 1 | 2 | 3 | 18330 |
| Итого (fy = fi) | 5 | 15 | 20 | 30 | 15 | 10 | 5 | 100 | 12700 |
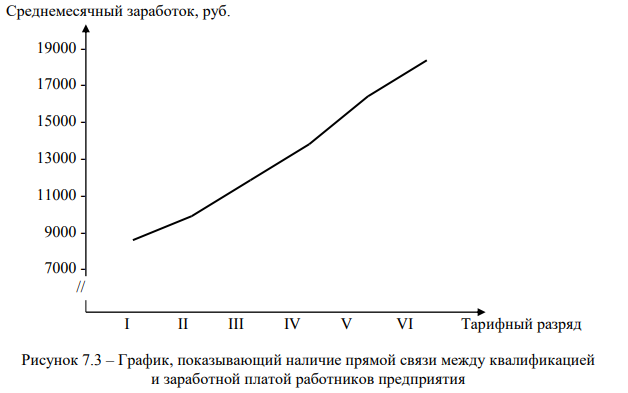
По данным таблицы 7.9 наблюдается наличие прямой корреляционной связи между квалификацией работников и их заработной платой.
Графически зависимость между квалификацией и заработком работников предприятия по данным таблицы 7.9 показана на рис. 7.3.
Аналитические группировки характеризуют только общие черты исследуемой связи между признаками, ее тенденцию, однако не дают количественной оценки силы связи. На основе аналитических группировок и корреляционных таблиц задача оценки тесноты связи между двумя коррелируемыми показателями решается при помощи расчета эмпирического корреляционного отношения, методика расчета которого рассмотрена в п. 5.4 (с. 83).
Уточним формулу 5.20 с учетом обозначений значений признаков, введенных в данной теме.
Эмпирическое корреляционное отношение рассчитывается по формуле:

где σ2м гр. и σ2y – соответственно, межгрупповая и общая дисперсии результативного признака.
Межгрупповая дисперсия результативного признака рассчитывается по формуле:

где n – число групп по факторному признаку х;
yj – среднее значение результативного признака по группам;
y – общее среднее значение результативного признака;
fj = fx – частота в i-й группе х.
Общая дисперсия результативного признака рассчитывается по формуле:

где m – число групп по результативному признаку у;
yi – индивидуальные значения результативного признака (середины интервалов);
fi = fy – частота в j-й группе у.
Пример расчета эмпирического корреляционного отношения
По данным таблицы 7.9 следует оценить тесноту связи между квалификацией работников предприятием и оплатой их труда.
Решение
По формуле 7.7 межгрупповая дисперсия заработной платы работников предприятия равна: 6768.
По формуле 7.8 общая дисперсия заработной платы работников предприятия равна: 8910.
По формуле 7.6 эмпирическое корреляционное отношение равно: 0,87, что свидетельствует о тесной связи между уровнем квалификации работников предприятия и их заработной платой (см. табл. 5.10).
Следует отметить, что η > 0 не является доказательством наличия корреляционной связи между признаками. Отличное от нуля корреляционное отношение может появиться при неправильном распределении исследуемой совокупности на группы.
Эмпирическое корреляционное отношение должно иметь высокий уровень надежности.
Для оценки надежности корреляционных характеристик (т.е. истинности причин отклонений групповых средних от общей средней) используют критерии Фишера (F-критерий) или Стьюдента (t-критерий), разработанные математической статистикой.
Критерий Фишера (FФ) определяется по формуле:

где σ2м гр. – межгрупповая дисперсия;
σ2ост – остаточная (средняя из внутригрупповых) дисперсия;
k1, k2 – степени свободы для межгрупповой и средней из внутригрупповых дисперсий.
Р. Фишер, английский статистик, установил распределение отношений дисперсий и разработал соответствующие математические таблицы (фрагмент такой таблицы приведен в таблице 7.10). В них приводится F-критерий теоретический (Fт) при двух вероятностях 0,95 и 0,99. Если Fф > Fт, то с принятой степенью вероятности можно утверждать о наличии влияния исследуемого фактора на результативный признак. Если же Fф ≤ Fт, можно утверждать, что разница между дисперсиями обусловлена влиянием случайных факторов.
Таблица 7.10
| k2 | k1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 20 | |
| 1 | 161,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234 | 238,9 | 242 | 248 |
| 2 | 18,51 | 19 | 19,16 | 19,25 | 19,3 | 19,33 | 19,37 | 19,39 | 19,44 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,78 | 8,66 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,96 | 5,8 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,74 | 4,56 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,06 | 3,87 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,63 | 3,44 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,34 | 3,15 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,13 | 2,93 |
| 10 | 4,96 | 4,1 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,97 | 2,77 |
| 11 | 4,82 | 3,98 | 3,59 | 3,63 | 3,2 | 3,09 | 2,95 | 2,86 | 2,65 |
| 12 | 4,75 | 3,88 | 4,49 | 3,26 | 3,11 | 3 | 2,85 | 2,76 | 2,54 |
| 14 | 4,6 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,7 | 2,6 | 2,39 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,49 | 2,28 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,41 | 2,19 |
| 20 | 4,35 | 3,49 | 3,1 | 2,87 | 2,71 | 2,6 | 2,45 | 2,35 | 2,12 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,16 | 1,93 |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,12 | 1,84 |
| 60 | 4 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,1 | 2,04 | 1,75 |
| 120 | 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,02 | 1,9 | 1,65 |
Распределение отношений дисперсий в таблицах Фишера для поиска Fт зависит от степеней свободы k1 и k2. В аналитической группировке они рассчитываются по формулам:
k1 = n - 1; (7.10)
k2 = N - n, (7.11)
где n – число групп по факторному признаку;
N – число единиц исследуемой совокупности.
К аналогичному выводу можно прийти при оценке надежности корреляционного отношения по критерию Стьюдента, который определяется по формуле:

где μη – средняя ошибка корреляционного отношения, рассчитываемая по формуле:

Если критерий Стьюдента tη ≥ 3, показатель корреляционного отношения считают вероятным (т.е. связь между исследуемыми явлениями доказана). Если tη < 3, то нельзя делать выводы о вероятности связи между исследуемыми явлениями.
Пример оценки степени надежности эмпирического корреляционного отношения с помощью критериев Фишера и Стьюдента
Необходимо проверить степень надежности эмпирического корреляционного отношения, рассчитанного по данным таблицы 7.9 в предыдущем примере.
Решение
Полученное по формуле 7.6 значение η = 0,87, позволило предположить наличие тесной связи между уровнем квалификации работников предприятия и их заработной платой.
По формуле 7.7 была рассчитана межгрупповая дисперсия месячного заработка работников предприятия (σ2м гр. = 6768), по формуле 7.8 – общая дисперсия (σ2y = 8910).
На основании правила сложения дисперсий (формула 5.18) найдем остаточную (среднюю их внутригрупповых) дисперсию: σ2ост = 8910 – 6768 = 2142.
Анализируемая совокупность включала 100 рабочих, для которых исследовалось наличие связи между их заработком и уровнем квалификации, отсюда N = 100. По уровню квалификации (тарифному разряду) было сформировано 6 групп, т. е. n = 6.
По формуле 7.10 рассчитаем значение степени свободы для межгрупповой дисперсии: k1 = 6 – 1 = 5.
По формуле 7.11 рассчитаем значение степени свободы для средней из внутригрупповых дисперсий: k2 = 100 – 6 = 94.
По формуле 7.9 значение критерия Фишера равно: 59,4.
С вероятностью 0,95 (при k1 = 5 и k2 = 94) F-критерий теоретический равен: Fт ≈ 2,29 (см. табл. 7.10). Так как Fф > Fт, то, с принятой степенью вероятности, можно утверждать о влиянии уровня квалификации работников предприятия на размер их заработной платы, т.е. о наличии связи между рассматриваемыми признаками работников предприятия.
По формуле 7.13 средняя ошибка корреляционного отношения равна: 0,024.
По формуле 7.12 значение критерия Стьюдента равно 36,25. Так как критерий Стьюдента tη ≥ 3, то связь между исследуемыми показателями (признаками) доказана.
Полученные значения критерия Фишера и критерия Стьюдента позволяют считать значение эмпирического корреляционного отношения 0,87 надежным для оценки тесноты связи между уровнем квалификации и заработком работников предприятия по данным таблицы 7.9.
Показатели тесноты связи между двумя атрибутивными признаками
Построение таблиц, в которых дается комбинационное распределение единиц совокупности по двум признакам применимо и к атрибутивным признакам. Взаимосвязи между атрибутивными признаками, их влияние на другие показатели, в том числе и количественные, особенно часто приходится изучать при проведении различных социологических исследований.
Простейшей формой таблицы взаимной сопряженности двух атрибутивных признаков является таблица «четырех полей» (четырехклеточная). В ней по каждому признаку выделяются только две группы, чаще всего по альтернативному принципу («да»-«нет», «хорошо»-«плохо» и т.д.).
Для измерения тесноты связи между двумя атрибутивными признаками, имеющими альтернативное выражение, используется коэффициент ассоциации, рассчитываемый с помощью таблицы взаимной сопряженности, которая состоит из четырех клеток, обозначенных латинскими буквами a, b, c, d. Каждая клетка таблицы соответствует определенной альтернативе того или иного признака, как это показано в таблице 7.11.
Таблица 7.11
| Признак | А | не А | ΣВ |
| В | a | b | а + b |
| не В | c | d | c + d |
| ΣА | a + c | b + d | a + b + c + d |
Коэффициент ассоциации (Касс) определяется по формуле:

Его существенный недостаток состоит в том, что если в одной из четырех клеток отсутствует частота (т.е. равна 0), коэффициент ассоциации всегда будет равен по модулю 1, и тем самым будет преувеличена мера действительной связи. Чтобы этого избежать, предложен другой показатель – коэффициент контингенции.
Коэффициент контингенции (Кконт) рассчитывается по формуле
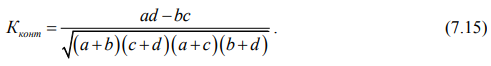
Коэффициент контингенции всегда меньше коэффициента ассоциации.
Связь считается достаточно значительной и подтвержденной, если |Касс| > 0,5 или |Кконт| >0,3.
Для исследования корреляции атрибутивных альтернативных признаков предложен также коэффициент колигации.
Коэффициент колигации (Ккол) рассчитывается по формуле:

Коэффициент колигации, как и коэффициент контингенции, оценивает связь между признаками более сдержанно, чем коэффициент ассоциации, причем всегда: Касс > Ккол > Кконт.
Пример расчета показателей тесноты связи между атрибутивными признаками
По результатам опроса студентов второго курса экономических специальностей, целью которого было выявление связи между курением студентов и курением родителей в их семьях, приведенным в таблице 7.12, необходимо оценить связь между курением родителей и их детей.
Таблица 7.12
| Семьи, в которых | Студенты, которые | Итого | |
|---|---|---|---|
| не курят | курят | ||
| родители не курят | 1 | 6 | 7 |
| родители курят | 8 | 1 | 9 |
| Итого | 9 | 7 | 16 |
Решение
По формуле 7.14: Касс = -0,96.
По формуле 7.15: Кконт = -0,75.
По формуле 7.16:
Ккол = -0,75.
Полученные значения коэффициентов ассоциации, контингенции и колигации свидетельствуют о наличии тесной связи между курением детей и их родителей. Правда, результаты опроса показали, что дети поступали с точностью «до наоборот»: в курящих семьях дети не курили и наоборот.
В том случае, когда оба взаимосвязанных признака разделены более чем на две группы, для измерения тесноты связи используются показатели взаимного сочетания (сопряжения), предложенные К. Пирсоном и А. Чупровым.
Коэффициент взаимной сопряженности Пирсона (КП) рассчитывается по формуле:
 где φ2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки, рассчитывается по формуле:
где φ2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки, рассчитывается по формуле:

Коэффициент взаимной сопряженности Чупрова (КЧ) рассчитывается по формуле:

где n1 и n2 – соответственно, количество групп в графах и количество групп в строках.
Результат оценки тесноты связи, полученный на основании коэффициента взаимной сопряженности Чупрова, более точен, поскольку он учитывает количество групп по каждому из исследуемых признаков. Его выгодно использовать и при большем разделении единиц совокупности на группы по взаимосвязанным признакам. Коэффициент взаимной сопряженности Пирсона используется в основном в случае квадратной таблицы, тогда как Чупрова – пригоден для измерения связи и в прямоугольных таблицах.
Считается, что уже при значении коэффициентов взаимной сопряженности 0,3 можно говорить о тесной связи между вариацией исследуемых признаков.
Пример расчета коэффициента взаимной сопряженности Чупрова
С помощью коэффициента взаимной сопряженности Чупрова необходимо определить тесноту связи между урожайностью зерновых культур сельскохозяйственных предприятий региона и их организационно-правовой формой по данным таблицы 5.11. Напомним, что рассчитанное в п. 5.4 по данным таблицы 5.11 эмпирическое корреляционное отношение (η = 0,66) характеризует связь между урожайностью зерновых культур сельскохозяйственных предприятий региона и их организационно-правовой формой как достаточно тесную.
Решение
Преобразуем таблицу 5.11 в более удобную для расчета коэффициента взаимной сопряженности Чупрова форму (таблица 7.13).
Таблица 7.13
| Группы предприятий | по урожайности зерновых культур (ц/га) | Итого | Средняя урожайность по группе, ц/га | |||||
|---|---|---|---|---|---|---|---|---|
| по организационно-правовой форме хозяйствования | 15,8- 18,97 | 18,97- 22,14 | 22,14- 25,31 | 25,31- 28,48 | 28,48- 31,65 | 31,65- 34,82 | ||
| 17,4 | 20,6 | 23,7 | 26,9 | 30,1 | 33,2 | |||
| Государственные предприятия | 2 | – | 3 | 1 | – | – | 6 | 22,14 |
| Общества с ограниченной ответственностью | 1 | 4 | 8 | 3 | 1 | – | 17 | 23,54 |
| Фермерские хозяйства | – | – | – | 3 | 3 | 1 | 7 | 29,16 |
| Итого | 3 | 4 | 11 | 7 | 4 | 1 | 30 | 24,57 |
По формуле 7.18 показатель средней квадратической сопряженности равен: φ2= 0,693.
По формуле 7.19 коэффициент взаимной сопряженности Чупрова равен: КЧ = 0,263. Так как это значение приближается к 0,3, то можно говорить о наличии достаточно тесной связи между урожайностью зерновых культур и организационно-правовой формой сельскохозяйственных предприятий, что подтверждает ранее сделанные выводы.
