Выборочный метод
Общая характеристика выборочного метода
Обобщающие статистические характеристики, как один из результатов статистического исследования, предполагают предварительный сбор данных в ходе статистического наблюдения.
Наиболее распространенным в практике несплошного статистического обследования является выборочный метод, при котором характеристика всей совокупности дается по некоторой ее части, отобранной в случайном порядке.
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. В частности, если проверка качества отдельных видов продукции может быть связана с ее уничтожением; исследуемые совокупности настолько велики, что было бы физически невозможно собрать данные в отношении каждого из их членов.
Выборочное наблюдение используют также для проверки результатов сплошного наблюдения.
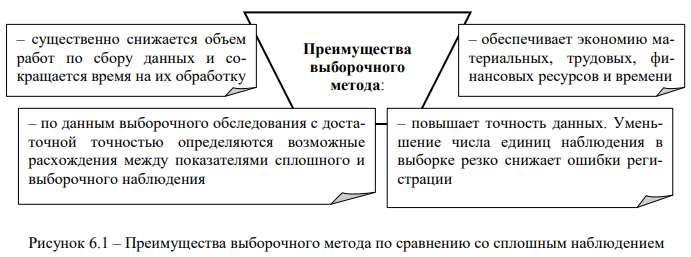
В случае научно обоснованного и достаточного отбора единиц, выборочный метод имеет ряд преимуществ по сравнению со сплошным наблюдением, приведенных на рис. 6.1.
Выборки используются как в официальной статистике, например в статистике населения, рынка труда, занятости и заработной платы, так и при социально-экономических исследованиях, в частности, при опросах общественного мнения и выяснении потребительских предпочтений, в маркетинговых исследованиях и т.д.
Совокупность, из которой производится отбор, называется генеральной совокупностью
Преимущества выборочного метода:
- существенно снижается объем работ по сбору данных и сокращается время на их обработку
- повышает точность данных. Уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации
- по данным выборочного обследования с достаточной точностью определяются возможные расхождения между показателями сплошного и выборочного наблюдения
- обеспечивает экономию материальных, трудовых, финансовых ресурсов и времени (N). Отобранные данные составляют выборочную совокупность (n). Как правило, объем выборки не должен быть менее 5 % генеральной совокупности.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки полно и адекватно представляет свойства генеральной совокупность, иначе говоря, от того, насколько выборка репрезентативна. Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц.
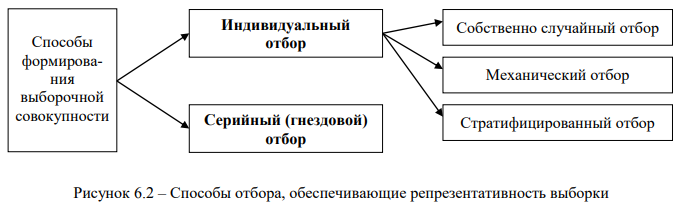
Различают два подхода к формированию выборочной совокупности, обеспечивающие репрезентативность выборки: индивидуальный отбор, включающий собственно случайный, механический и стратифицированный отбор, и серийный отбор, схематично представленные на рис. 6.2.
Собственно случайный отбор, или случайная выборка, осуществляется с помощью жеребьевки либо по таблице случайных чисел.
В первом случае всем элементам генеральной совокупности присваивается порядковый номер и на каждый элемент заводится жребий – пронумерованные шары или карточки-фишки, которые перемешиваются и помещаются в ящик, из которого затем отбираются на удачу.
Во втором случае производится выбор случайных чисел из специальных таблиц, образующих порядковые номера для отбора. Для удобства чтения числа в таблицах обычно печатаются в виде блоков цифр, причем эти объединения в блоки не имеют статистического значения. Так, это могут быть числа: 5489, 5583, 3156, 0835, 1988, 3912 и т.д. Чтобы произвести отбор по таблице случайных чисел, нужно выбрать начальную точку, например, закрыв глаза и поставив наугад точку в таблице карандашом. Единица с выпавшим номером будет являться первой в выборке.
Применение комбинаций цифр в таблице случайных чисел зависит от размера совокупности: если в совокупности 1000 единиц, то порядковый номер каждой единицы должен состоять из трех цифр от 000 до 999. В данном случае приведенные выше случайные числа дали бы первые 8 номеров единиц выборочной совокупности: 548, 955, 833, 156, 083, 519, 833, 912. Дополнительные номера могут быть получены из последующих блоков тем же способом. Процесс формирования случайных чисел и определения номера отбираемой единицы продолжается до тех пор, пока не будет получен заданный объем выборочной совокупности.
Несколько сложнее выглядит процедура назначения номеров, отбираемых в выборочную совокупность, для случая произвольного объема генеральной совокупности. В данном случае из случайных чисел таблиц формируется последовательность случайных величин, равномерно распределенных в интервале от 0 до 1. В рассматриваемом примере такими числами можно было бы считать 0,5489; 0,5583; 0,3156; 0,0835; 0,1988; 0,3912 и т. д. Предположим, что генеральная совокупность состоит из 7328 единиц. Тогда, в выборочную совокупность должны войти единицы с номерами: 7328 × 0,5489 = 4022; 7328 × 0,5583 = 4091; 7328 × 0,3156 = 2313; 7328 × 0,0835 = 612; 7328 × 0,1988 = 1457; 7328 × 0,3912 = 2867.
При механическом способе отбора отбирается каждый (N/n)-й элемент генеральной совокупности. N/n – шаг механического отбора. Если единицы в совокупности не ранжированы относительно изучаемого признака, то первый элемент выбирается наугад, произвольно, а если ранжированы, то из середины первой группы, т. е. отступив полшага.
Механическое формирование выборочной совокупности, не связанное с процедурами получения случайных чисел, наиболее часто применяют на практике.
При стратифицированном (расслоенном) отборе генеральную совокупность предварительно разбивают на однородные группы с помощью типологической группировки, после чего производят отбор единиц из каждой группы в выборочную совокупность случайным или механическим способом. Этот метод гарантирует, что единицы разных групп (слоев) включаются в выборку пропорционально их численности в генеральной совокупности, т. е. выборка отражает структуру генеральной совокупности. Стратифицированный способ отбора применяется при отборе единиц из неоднородной совокупности.
При серийном отборе в порядке случайной или механической выборки выбирают не единицы, а определенные районы, серии (гнезда), внутри которых производится сплошное наблюдение.
Особенности обследуемых объектов определяют два метода отбора единиц в выборочную совокупность – повторный и бесповторный.
При повторном отборе (отборе по схеме возвращенного шара) каждая попавшая в выборку единица или серия возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность всех единиц генеральной совокупности остается одинаковой.
Бесповторный отбор (отбор по схеме невозвращенного шара) означает, что каждая отобранная единица (или серия) не возвращается в генеральную совокупность и не может подвергаться вторичной регистрации, а потому для остальных единиц вероятность попасть в выборку увеличивается. Бесповторный отбор дает более точные результаты по сравнению с повторным, так как при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности. Поэтому он находит более широкое применение в статистической практике. И только в тех случаях, когда бесповторный отбор провести нельзя, используется повторная выборка (при обследовании потребительского спроса, пассажирооборота и т. п.).
Ошибки выборки
На основании зарегистрированных в соответствии с программой статистического наблюдения значений признаков единиц выборочной совокупности, рассчитываются обобщающие выборочные характеристики:
- выборочная средняя (х~);
- выборочная доля (w) единиц, обладающих каким-либо интересующим исследователей признаком, в общей их численности.
Доля единиц, являющихся носителем определенного признака в генеральной совокупности, обозначается р.
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки.
Ошибки выборки, как ошибки любого другого вида статистического наблюдения, подразделяются на ошибки регистрации и ошибки репрезентативности. Основной задачей выборочного метода является изучение и измерение случайных ошибок репрезентативности.
Пример расчета ошибок репрезентативности показателей выборки
В таблице 6.1 представлено распределение студентов по уровню успеваемости в генеральной и двух десятипроцентных выборочных совокупностях.
Следует определить ошибки выборки для средней и для доли, т.е. насколько выборочный средний балл успеваемости и выборочная доля студентов, получивших при тестировании оценки «хорошо» и «отлично», отличаются от среднего балла успеваемости и доли хорошо и отлично успевающих студентов, рассчитанных по данным генеральной совокупности.
Таблица 6.1
| Оценка | Число студентов, чел. | ||
|---|---|---|---|
| Генеральная совокупность | Первая выборка | Вторая выборка | |
| Неудовлетворительно | 100 | 9 | 12 |
| Удовлетворительно | 300 | 27 | 29 |
| Хорошо | 520 | 54 | 52 |
| Отлично | 80 | 10 | 7 |
| Всего | 1000 | 100 | 100 |
Решение
Ошибки репрезентативности среднего балла успеваемости студентов, исчисленного по данным выборок, и выборочной доли студентов, получивших при тестировании оценки «отлично» и «хорошо», определяются на основе расхождений между соответствующими выборочными и генеральными показателями.
Средний балл тестирования студентов рассчитывается по формуле средней арифметической взвешенной (4.22).
По генеральной совокупности средний балл равен: x = 3,58; по первой выборке x1 = 3,65; по второй выборке x2 = 3,54.
Доля студентов, получивших оценки «хорошо» и «отлично», рассчитывается по формуле 4.11.
По генеральной совокупности она равна: p=0,6 или 60 %; по первой выборке – w1 = 0,64 или 64 %; по второй выборке – w2 = 0,59 или 59 %.
Ошибки репрезентативности для средней:
– по первой выборке: x1 - x = 3,65 – 3,58 = +0,07;
– по второй выборке: x2 - x = 3,54 – 3,58 = -0,04.
Ошибки репрезентативности для доли:
- по первой выборки: w1 – р = 0,64 – 0,6 = +0,04;
- по второй выборки: w2 – р = 0,59 – 0,6 = -0,01.
Таким образом, по результатам обработки данных первой выборки получили, что средний балл успеваемости студентов на 0,07 выше, чем средний балл, исчисленный по генеральной совокупности, и, соответственно, доля студентов, получивших при тестировании оценки «хорошо» и «отлично» на 0,04 долей единицы выше, чем этот же показатель в генеральной совокупности. Во второй выборке показатели средней и доли, соответственно, на 0,04 балла и 0,01 долей единицы ниже, чем в генеральной совокупности.
Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок.
Средняя ошибка выборки для средней величины (μx) рассчитывается по формуле:

где σх – среднее квадратическое отклонение значений признака х от его средней величины; n – объем (число единиц) выборочной совокупности.
Средняя ошибка выборки для доли единиц определенных значений признака (μp) рассчитывается по формуле:

В формулах 6.1 и 6.2, соответственно, σх2 и р×(1 – р) являются характеристиками генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность при ее большом объеме достаточно точно воспроизводит характеристики генеральной совокупности.
Формулы для расчета средних ошибок выборки для средней и для доли при повторном и бесповторном методах отбора, приведены в таблице 6.2.
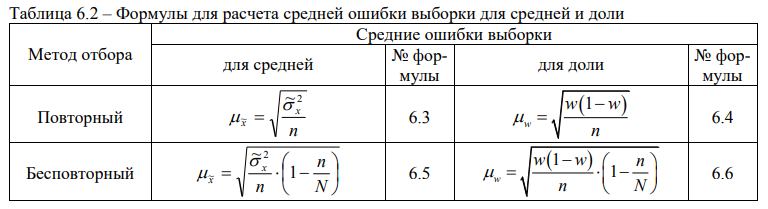
Величина (1 - n/N) всегда меньше единицы, поэтому величина средней ошибки выборки при бесповторном отборе оказывается меньше, чем при повторном отборе. В тех случаях, когда доля выборки незначительна и множитель (1 - n/N) близок к единице, поправкой можно пренебречь.
Пример расчета средних ошибок выборки
По данным таблицы 6.1 следует определить средние ошибки для выборочной средней оценки тестирования студентов и для выборочной доли студентов, получивших «хорошо» и «отлично», при повторном и бесповторном способах отбора студентов в первую выборочную совокупность.
Решение
По формуле 5.7 дисперсия оценок, полученных студентами первой выборочной совокупности, равна: 0,6.
При повторном отборе средняя ошибка оценки тестирования студентов первой выборки (для среднего балла успеваемости), рассчитанная по формуле 6.3, равна: 0,08 (балла), а средняя ошибка для доли студентов, получивших при тестировании «хорошо» и «отлично», в первой выборке по формуле 6.4 равна: 0,048 (4,8%).
При бесповторном отборе средняя ошибка оценки тестирования студентов первой выборки, рассчитанная по формуле 6.5, равна: 0,07 (балла), а средняя ошибка для доли студентов, получивших при тестировании «хорошо» и «отлично», в первой выборке по формуле 6.6, равна: 0,046 (4,6 %).
Утверждать, что генеральная средняя значения признака или генеральная доля не выйдет за границы средней ошибки выборки можно лишь с определенной степенью вероятности. Поэтому, для характеристики ошибки выборки кроме средней ошибки рассчитывается предельная ошибка выборки (Δ), которая зависит от уровня вероятности, гарантирующего, что предельная ошибка не превысит t-кратную среднюю ошибку.
Уровень вероятности (Р) определяет величина нормированного отклонения (t), и наоборот.
Наиболее часто используемые сочетания t и Р приведены в таблице 6.3.
Таблица 6.3
| t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
| Р | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
Нормированное отклонение t – коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t-кратную среднюю ошибку. Этот коэффициент показывает, сколько средних ошибок содержится в предельной ошибке. Так, если t = 1, то с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки.
Формулы для расчета предельных ошибок выборки приведены в таблице 6.4.

После расчета предельных ошибок выборки находят доверительные интервалы для генеральных показателей.
Вероятность, которая принимается при расчете ошибки выборочной характеристики, называется доверительной. Доверительный уровень вероятности 0,95 означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы; вероятности 0,954 – в 46 случаях из 1000, а при 0,999 – в 1 случае из 1000.
Для генеральной средней наиболее вероятные границы, в которых она будет находиться с учетом предельной ошибки репрезентативности, будут определяться следующим образом:

Наиболее вероятные границы, в которых будет находиться генеральная доля, будут определяться следующим образом:

Формулы 6.7-6.10 применяются при определении ошибок выборки, осуществляемой собственно случайным и механическим методами.
Пример расчета предельных ошибок выборки и доверительных интервалов для характеристик генеральной совокупности
По данным первой выборочной совокупности студентов, проходивших тестирование, (см. табл. 6.1) определим с вероятностью 0,954 пределы (доверительные интервалы), в которых находится средний балл студентов генеральной совокупности и доля студентов в общей численности студентов генеральной совокупности, получивших при тестировании «хорошо» и «отлично». Отбор студентов был проведен методом случайной бесповторной выборки.
Решение
По данным таблицы 6.3 коэффициент доверия t, показывающий, сколько с вероятностью 0,954 средних ошибок содержится в предельной ошибке, равен 2, т.е. предельная ошибка выборки с вероятностью 0,954 не превысит двух средних ошибок.
По формуле 6.9 предельная ошибка выборочной средней с вероятностью 0,954 будет равна 0,146 (балла), а границы, в которых будет находиться средний балл тестирования студентов генеральной совокупности, в соответствии с выражением 6.11, имеют вид 3,65-0,15 ≤ x ≤ 3,65+0,15, т.е. 3,5 ≤ x ≤ 3,8 или средний балл тестирования студентов генеральной совокупности будет находиться в пределах от 3,5 до 3,8 баллов.
По формуле 6.10 предельная ошибка выборочной доли студентов, получивших при тестировании «хорошо» и «отлично», с вероятностью 0,954 будет равна: Δw = 0,092, а границы, в которых будет находиться доля студентов аттестованных на «хорошо» и «отлично» в генеральной совокупности, в соответствии с выражением 6.12, будут равны: 0,64-0,092 ≤ р ≤ 0,64 + 0,092, т.е. 0,548 ≤ р ≤ 0,732. Таким образом, доля студентов генеральной совокупности, протестированных на «хорошо» и «отлично», будет находиться в пределах от 54,8 до 73,2 процентов.
При стратифицированном отборе в выборку обязательно попадают представители всех групп и обычно в тех же пропорциях, что и в генеральной совокупности. Поэтому ошибка выборки в данном случае зависит, в основном, от средней из внутригрупповых дисперсий. Исходя из правила сложения дисперсий можно сделать вывод, что ошибка выборки для стратифицированного отбора всегда будет меньше, чем для собственно случайного отбора.
При серийном (гнездовом) отборе мерой колеблемости будет межгрупповая дисперсия.
Определение численности выборки
Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность средней и доли.
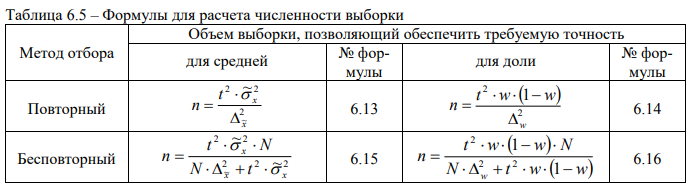
Формулы для определения объема (численности) выборки, позволяющего обеспечить требуемую точность значений соответствующих показателей, в зависимости от метода отбора для средней и доли приведены в таблице 6.5. Они следуют из формул предельных ошибок выборки.
Формулы 6.13-6.16 используются для определения численности выборки при собственно случайном и механическом отборе.
Пример расчета численности выборки, обеспечивающей заданную точность результатов исследования, формируемой посредством случайного бесповторного отбора
Как и в предыдущих примерах, рассмотрим результаты тестирования 1000 студентов. В порядке случайной бесповторной выборки предлагается определить средний балл тестирования при условии, что ошибка выборочной средней не должна превысить 0,2 балла с вероятностью 0,997 и при среднем квадратическом отклонении 0,5 балла. Кроме того, предполагается определить долю студентов получивших при тестировании «хорошо» и «отлично», при условии, что в выборочной совокупности доля студентов аттестованных на «хорошо» и «отлично» составит 30%, а предельная ошибка для доли с вероятностью 0,997 не превысит 5%.
Следует определить, какова должна быть численность студентов, попавших в выборочную совокупность, позволяющая обеспечить заданную точность среднего балла тестирования и доли студентов, результат тестирования которых составил «хорошо» и «отлично».
Решение
По данным таблицы 6.3 коэффициент доверия t, показывающий, сколько с вероятностью 0,997 средних ошибок содержится в предельной ошибке, равен 3.
По формуле 6.15 число студентов, которое следует включить в выборочную совокупность для того, чтобы обеспечить заданную точность среднего балла тестирования, при бесповторном отборе равно: 53 чел., т.е. для того, чтобы средний балл тестирования студентов с вероятностью 0,997 при условии бесповторного отбора, в выборку должно быть включено 53 студента.
По формуле 6.16 число студентов, которое следует включить в выборочную совокупность для того, чтобы обеспечить заданную точность доли студентов, получивших при тестировании «хорошо» и «отлично», при бесповторном отборе равно: 431 чел. Таким образом, для того, чтобы доля студентов, получивших при тестировании «хорошо» и «отлично» с вероятностью 0,997 была равна p = w ± 5 = 30 ± 5% при бесповторном отборе, в выборку должен быть включен 431 студент.
Значения Δ и t определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки, и наоборот. Например, увеличение ошибки выборки в 2 раза уменьшит численность выборки n в 4 раза.
Вариация (σ2) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна.
Приближенно σ2 определяют следующими способами:
- берут из предыдущих исследований;
- устанавливается исходя из того, что общий размах вариации укладывается в 6 сигм (R ≈ 6σ), σ ≈ R/6. Для большей точности R делят на 5;
- если хотя бы приблизительно известна средняя величина изучаемого признака, то σ ≈ x/3;
- исходя из того, что при большой численности выборочной совокупности сомножитель (n-1)/n ≈1, можно принять выборочную дисперсию в качестве генеральной дисперсии, и наоборот.
При стратифицированном отборе, не пропорциональном объему групп, общее число отбираемых единиц делится на количество групп. Полученная величина даст объем выборки из каждой группы.
При стратифицированном отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется по формуле:

где ni – объем выборки из i-й группы;
n – общий объем выборки;
Ni – объем i-й группы генеральной совокупности;
N – объем генеральной совокупности.
При серийном (гнездовом) отборе необходимую численность отбираемых серий определяют так же, как и при собственно случайном, только вместо N, n, σ2 подставляют R, r и σ2м. гр, где R – число серий в генеральной совокупности; r – число отобранных серий; σ2м. гр – межсерийная (межгрупповая) дисперсия.
Пример расчета численности стратифицированной выборки, а также границ, в которых находится среднее значение признака единицы генеральной совокупности
В условном регионе проживает десять тысяч семей, из которых в 5000 семей трудоспособные члены семьи заняты в промышленности, в 4000 семей – в сельским хозяйством и в 1000 семей – в нематериальной сфере (в сфере различных услуг). Для определения среднего числа детей в семье, в регионе была проведена десятипроцентная стратифицированная выборка с отбором единиц пропорционально численности групп, сформированных по принадлежности их трудоспособных членов к определенным сферам экономики. Внутри групп применялся механический отбор.
В таблице 6.6 приведены данные о числе семей в генеральной совокупности, сгруппированных по принадлежности их работающих членов к той или иной отрасли экономики, а также о среднем числе детей в семьях региона и их вариации, рассчитанные по соответствующим выборочным совокупностям.
Необходимо с вероятностью 0,997 определить пределы, в которых находится среднее число детей в семье в регионе.
Таблица 6.6
| Группы семей по принадлежности их трудоспособных членов к отраслям экономики | Число семей в генеральной совокупности | Среднее число детей в семье, чел. | Среднее квадратическое отклонение, чел. |
|---|---|---|---|
| Промышленность | 5000 | 2,3 | 1,2 |
| Сфера услуг | 1000 | 1,8 | 0,5 |
| Сельское хозяйство | 4000 | 2,8 | 2,5 |
| Всего | 10000 | – | – |
Решение
Численность стратифицированной выборки будет равна 1000 семей.
По формуле 6.17 объем выборки в каждой типологической группе равен: n1 = 500 семей; n2 = 100 семей; n3 = 400 семей.
По формуле 4.22 выборочное среднее значение числа детей в семьях региона равно: 2,45 чел.
По формуле 5.17 среднее значение внутригрупповых дисперсий равно 3,24.
По формуле 6.9 найдем предельную ошибку выборочной средней при стратифицированном отборе единиц совокупности = 0,16 чел.
Таким образом, с вероятностью 0,997 можно утверждать, что в регионе среднее число детей в семье находится в пределах 2,45 - 0,16 ≤ x ≤ 2,45 + 0,16 или 2,3 ≤ x ≤ 2,6.
