Статистические показатели
Общая характеристика статистического показателя
На этапе статистической сводки от индивидуальных значений признаков единиц совокупности переходят к обобщающим характеристикам свойств исследуемых совокупностей или их частей – показателям.
Под статистическим показателем понимается количественная характеристика изучаемого объекта (социально-экономического явления) или его свойства.
Поскольку статистика изучает массовые явления, статистический показатель – это обобщающая характеристика какого-то свойства совокупности, группы. Этим он отличается от индивидуальных значений, которые, как отмечалось, называются признаками. Например, средняя продолжительность ожидаемой жизни родившегося поколения людей в стране – статистический показатель, продолжительность жизни конкретного человека – признак.
Основные характеристики статистического показателя представлены на рис. 4.1.
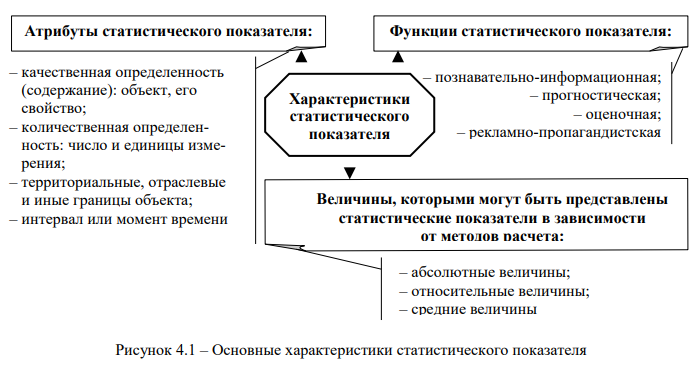
Статистический показатель всегда имеет качественную определенность (содержание), т.е. характеризует социально-экономические явления и свойственные им категории или признаки. Как количественная характеристика исследуемого явления он имеет числовое значение и соответствующие единицы измерения. Количественные размеры статистического показателя зависят от территориальных, отраслевых и иных границ объекта и времени исследования. В частности, валовой внутренний продукт (ВВП) Российской Федерации за 2018 год, как статистический показатель, характеризуется следующим образом:
- его качественная определенность состоит в том, что ВВП отражает рыночную стоимость всех товаров и услуг, предназначенных для конечного потребления и произведенных на территории страны за определенный период времени;
- его количественная определенность состоит в том, что ВВП равен 103 трлн. 626,6 млрд. рублей;
Атрибуты статистического показателя:
Величины, которыми могут быть представлены статистические показатели в зависимости от методов расчета:
- качественная определенность (содержание): объект, его свойство;
- количественная определенность: число и единицы измерения;
- территориальные, отраслевые и иные границы объекта;
- интервал или момент времени
- познавательно-информационная;
- прогностическая;
- оценочная;
- рекламно-пропагандистская
Характеристики статистического показателя
Функции статистического показателя:
- абсолютные величины;
- относительные величины;
- средние величины
- его территориальные границы определены границами Российской Федерации;
- его временной интервал соответствует 2018 году.
Статистический показатель выполняет познавательно-информационную; прогностическую; оценочную и рекламно-пропагандистскую функции.
В зависимости от методов расчета статистические показатели могут быть абсолютными, относительными и средними величинами.
Абсолютные величины
Изучая массовые общественные явления, статистика в своих выводах опирается на числовые данные, полученные в конкретных условиях места и времени.
Основой всех форм учета и приемов количественного анализа являются абсолютные величины, отражающие уровень развития явления (его размер или объем).
В статистике абсолютные величины:
- являются поименованными, т.е. имеют наименования;
- измеряются в конкретных единицах (рублях, штуках, человеко-часах и т.д.);
- в отличие от математического понятия абсолютной величины, могут быть как положительными, так и отрицательными, например: убытки, потери и т. п.
Единицы измерения абсолютных величин могут быть натуральными, трудовыми, демографическими и стоимостными.
Натуральные единицы измерения используются для определения количества соответствующих единиц совокупности, веса, объема, расстояния и т.д. Они могут быть простыми (т, м, км, шт.), сложными, представляющими собой комбинацию двух разноименных величин (например, киловатт-час, тонно-километр), и условными (условно-натуральными).
Условно-натуральные единицы измерения применяют для получения суммарных абсолютных величин в случае, когда индивидуальные величины характеризуют разновидности продукции, близкие по своим потребительским свойствам, но различающиеся, например, объемом упаковки, жирностью, калорийностью, удельной теплотворностью и т.д.
Для получения условно-натуральных единиц измерения определяют коэффициенты пересчета (перевода) натуральных единиц измерения в условно-натуральные.
Для определения коэффициентов пересчета одна из разновидностей продукции по своим потребительским свойствам или другим значимым характеристикам принимается за условную единицу и с ее параметрами соотносятся значения аналогичных индивидуальных показателей схожей продукции.
Рассчитанные коэффициенты умножают на количество каждой разновидности продукции и путем суммирования получают их общую абсолютную величину в условно-натуральных единицах измерения.
Пример расчета абсолютных величин в условно-натуральных единицах измерения
Консервный завод выпускает разные по емкости банки консервов. Поэтому простой их подсчет в штуках (физических банках) не даст правильного представления об объеме производства в натуральном выражении. Продукцию консервных заводов принято измерять в тубах, т. е. в тысячах условных банок. За условную банку принята банка № 8 емкостью 353,4 см3. Значит, если выпущено 300 тысяч банок консервов емкостью 801,0 см3(банок № 3), то объем производства составит 678 туб (300 × 2,26, где 2,26 – коэффициент перевода банок № 3 в условно-натуральные банки № 8; 2,26 = 801,0 : 353,4).
Демографические и трудовые единицы измерения используются для показателей, характеризующих численность населения, его состав, трудовые ресурсы, а также затраты труда на производство продукции (чел., человеко-день, человеко-час).
Стоимостные (денежные) единицы измерения используются для характеристики многих стоимостных показателей: товарной продукции, заработной платы, прибыли и т.п. Эти единицы измерения являются универсальными, т.е. с их помощью можно обобщить разнородные натуральные единицы измерения.
С точки зрения конкретного исследования совокупность абсолютных величин может состоять из показателей индивидуальных, характеризующих размер признака у отдельных единиц совокупности, и суммарных, характеризующих итоговое значение признака по определенной части или всей совокупности. Таким образом, суммарные (итоговые) показатели могут быть как групповыми, так и общими по всей совокупности.
Отметим, что сама по себе абсолютная величина не дает полного представления об изучаемом явлении, так как ее уровень зависит от многих факторов, и, что воспринимается как «много», в одном случае, может показаться как «мало» в другом. Вопрос слоненка, обращенный к попугаю в рассказе Г. Остера «Как лечить удава», «три ореха – это куча?», отлично характеризует оценочную неоднозначность абсолютных величин.
Кроме того, абсолютная величина не позволяет оценить структуру исследуемого явления, соотношение между отдельными его частями, развитие во времени и т.д.
Относительные величины
Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых величин.
Знаменатель отношения, т.е. та величина, с которой сравнивают другую величину, называется основанием или базой сравнения.
В зависимости от базы сравнения относительные величины могут быть выражены в форме:
- коэффициентов, если база сравнения принята за 1;
- процентов (%), если база сравнения принята за 100;
- промилле (‰), если база сравнения принята за 1000;
- продецимилле (о/ооо), если база сравнения принята за 10000.
Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями.
По содержанию выражаемых количественных соотношений выделяют следующие виды относительных величин:
- относительная величина динамики;
- относительная величина задания (планового задания);
- относительная величина выполнения задания;
- относительная величина структуры;
- относительная величина координации;
- относительная величина сравнения;
- относительная величина интенсивности.
Относительная величина динамики характеризует изменение уровня развития какоголибо явления во времени и может быть выражена коэффициентом (индексом) роста, темпом роста или темпом прироста.
Коэффициент (индекс) роста (kр (iр)) получается в результате деления уровня показателя в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент, и рассчитывается, например, по формуле:
kр = Ф1 / Ф0, (4.1)
где Ф1 и Ф0 – соответственно фактические уровни показателя в текущем и предыдущем периодах.
Темп роста (Тр) – это коэффициент роста, выраженный в процентах, рассчитывается по формуле:
Тр = kр * 100, (4.2)
Темп прироста (Тпр) – разность между величиной темпа роста и 100 %, рассчитывается по формуле:
Тпр = Тр - 100, (4.3)
Пример расчета относительных величин динамики
В таблице 4.1 приведены показатели, частично характеризующие социально-экономическое развитие Республики Крым и г. Севастополя в 2017 и 2018 годах. По ее данным следует охарактеризовать динамику доходов и расходов бюджета Республики Крым в 2018 году по сравнению с 2017 годом.
Таблица 4.1
| Показатель | 2017 г. | 2018 г. | |
|---|---|---|---|
| факт | план | факт | |
| Доходы бюджета Республики Крым, всего, млн. руб. | 148170,2 | 170812,8 | 161686,4 |
| в том числе: | |||
| – налоговые доходы | … | 36435,4 | 36246,5 |
| – неналоговые доходы | … | 4114,5 | 4408,0 |
| – безвозмездные поступления | … | 130262,9 | 121031,9 |
| Расходы бюджета Республики Крым, млн. руб. | 149100,6 | 172682,0 | 161382,5 |
| Расходы консолидированного бюджета, млн. руб.: | |||
| – Республики Крым | 161718,1 | 187484,4 | 175470,5 |
| – г. Севастополя | 33549,5 | … | 35713,5 |
| Среднегодовая численность населения Республики Крым, тыс. чел. | 1912,9 | – | 1913,5 |
| Валовой региональный продукт Республики Крым, млн. руб. | 382355,0 | – | 415880,0 |
Примечание: Консолидированный бюджет субъекта РФ – это свод бюджетов всех уровней на соответствующей территории (в частности, бюджетов муниципальных образований и республиканского).
Решение
Решение задачи оформлено с помощью таблицы 4.2.
Таблица 4.2
| Показатель | Формула | Расчет | Значение |
|---|---|---|---|
| Коэффициент роста доходов бюджета РК (kр) | 4.1 | 161686,4 : 148170,2 | 1,091 |
| Темп роста доходов бюджета РК (Тр), % | 4.2 | 1,091 × 100 | 109,1 |
| Темп прироста доходов бюджета РК (Тпр), % | 4.3 | 109,1 – 100 | 9,1 |
| Коэффициент роста расходов бюджета РК (kр) | 4.1 | 161382,5 : 149100,6 | 1,082 |
| Темп роста расходов бюджета РК (Тр), % | 4.2 | 1,082 × 100 | 108,2 |
| Темп прироста расходов бюджета РК (Тпр), % | 4.3 | 108,2 – 100 | 8,2 |
Таким образом, по данным таблицы 4.2 видно, что фактические доходы бюджета Республики Крым в 2018 году по сравнению с 2017 годом выросли в 1,091 раза, т.е. их темп роста в обусловленный период составил 109,1%. Это означает, что доходы бюджета Республики за рассматриваемый период выросли на 9,1%. Соответственно, фактические расходы бюджета Республики Крым в 2018 году по сравнению с 2017 годом выросли в 1,082 раза, т.е. их темп роста составил 108,2 %, а темп прироста – 8,2 %.
Относительная величина планового задания характеризует изменение планового уровня показателя на предстоящий период по сравнению с фактически сложившимся его уровнем в предыдущем периоде и может быть представлена коэффициентом (индексом) планового роста, плановым темпом роста и плановым темпом прироста.
Коэффициент (индекс) планового роста (kр.пл.з (iр.пл.з)) представляет собой отношение уровня показателя, запланированного на предстоящий период, к уровню этого же показателя, фактически сложившемуся в предыдущем периоде и рассчитывается по формуле:
kр.пл.з = П1 / Ф0, (4.4)
где П1 – уровень показателя, запланированный на текущий (предыдущий) период.
Плановый темп роста (Тр.пл.з) – это коэффициент планового роста, выраженный в процентах, рассчитывается по формуле:
Тр.пл.з = kр.пл.з × 100. (4.5)
Плановый темп прироста (Тпр.пл.з) – разность между величиной планового темпа роста и 100% , рассчитывается по формуле:
Тпр.пл.з - 100. (4.6)
Пример расчета относительных величин планового задания
По данным таблицы 4.1 следует охарактеризовать плановые показатели доходов и расходов бюджета Республики Крым в 2018 году по сравнению с их фактическим уровнем, сложившимся в 2017 году.
Решение
Решение задачи оформлено с помощью таблицы 4.3.
Таблица 4.3
| Показатель | Формула | Расчет | Значение |
|---|---|---|---|
| Коэффициент планового роста доходов бюджета РК (kр.пл.з) | 4.4 | 170812,8 : 148170,2 | 1,153 |
| Плановый темп роста доходов бюджета РК (Тр.пл.з), % | 4.5 | 1,153 × 100 | 115,3 |
| Плановый темп прироста доходов бюджета РК (Тпр.пл.з), % | 4.6 | 115,3 – 100 | 15,3 |
| Коэффициент планового роста расходов бюджета РК (kр.пл.з) | 4.4 | 172682,0 : 149100,6 | 1,158 |
| Плановый темп роста расходов бюджета РК (Тр.пл.з), % | 4.5 | 1,158 × 100 | 115,8 |
| Плановый темп прироста расходов бюджета РК (Тпр.пл.з), % | 4.6 | 115,8 – 100 | 15,8 |
Данные таблицы 4.3 свидетельствуют о том, что доходы и расходы бюджета Республики Крым планировалось в 2018 году по сравнению с их фактическим уровнем 2017 года увеличить, соответственно, в 1,153 и 1,158 раза. Это означает, что плановый темп прироста составлил, соответственно, 115,3% и 115,8%. Таким образом, планировалось в 2018 году по сравнению с 2017 годом увеличить доходы республиканского бюджета на 15,3%, а его расходы на 15,8%, т.е. практически пропорционально.
Относительная величина выполнения задания характеризует степень выполнения задания (плана) и может быть выражена коэффициентом (индексом) выполнения задания (плана), процентом выполнения задания (плана) и процентом перевыполнения задания (плана).
Коэффициент (индекс) выполнения планового задания (kвып.пл.з (iвып.пл.з)), представляет собой отношение уровня показателя, фактически достигнутого в текущем периоде, к запланированному, и рассчитывается по формуле:
kвып.пл.з = Ф1 / П1. (4.7)
Процент выполнения планового задания (%вып.пл.з) – это коэффициент выполнения планового задания, выраженный в процентах, рассчитывается по формуле:
%вып.пл.з = kвып.пл.з × 100. (4.8)
Процент перевыполнения планового задания (%перевып.пл.з) рассчитывается по формуле:
%перевып.пл.з = %вып.пл.з - 100. (4.9)
Пример расчета относительных величин выполнения планового задания
По данным таблицы 4.1 следует охарактеризовать выполнение плана по доходам и расходам бюджета Республики Крым в 2018 году.
Решение
Решение задачи оформлено с помощью таблицы 4.4.
Таблица 4.4
| Показатель | Формула | Расчет | Значение |
|---|---|---|---|
| Коэффициент выполнения планового задания по доходам бюджета РК (kвып.пл.з) | 4.7 | 161686,4 : 170812,8 | 0,947 |
| Процент выполнения планового задания по доходам бюджета РК (%вып.пл.з), % | 4.8 | 0,947 × 100 | 94,7 |
| Процент перевыполнения планового задания по доходам бюджета РК (%перевып.пл.з), % | 4.9 | 94,7 – 100 | -5,3 |
| Коэффициент выполнения планового задания по расходам бюджета РК (kвып.пл.з) | 4.7 | 161382,5 : 172682,0 | 0,935 |
| Процент выполнения планового задания по расходам бюджета РК ((%вып.пл.з), % | 4.8 | 0,935 × 100 | 93,5 |
| Процент перевыполнения планового задания по расходам бюджета РК (%перевып.пл.з), % | 4.9 | 93,5 – 100 | -6,5 |
Таким образом, процент выполнения плана доходов и расходов бюджета Республики Крым составил в 2018 году, соответственно, 94,7% и 93,5%. Это свидетельствует о невыполнении плана по формированию доходов на 5,3%, в свою очередь, фактические расходы бюджета оказались на 6,5% ниже плановых.
Относительные величины динамики, планового задания и выполнения плана связаны соотношением, представленным формулой:
kp = kp.пл.з kвып.пл.з. (4.10)
Данное равенство подтверждается значениями соответствующих показателей, приведенных в таблицах 4.2-4.4. В частности, относительно доходов бюджета Республики Крым в 2017-2018 гг.: 1,091 = 1,153 × 0,947 = 1,092; относительно его расходов: 1,082 = 1,158 × 0,935 = 1,083. Разница в значениях показателей возникла за счет округлений.
Представленная модель позволяет рассчитать неизвестное значение одного из трех приведенных в формуле 4.10 показателей при наличии данных о значения двух других.
Пример расчета показателей, основанного на взаимосвязи относительных величин динамики, планового задания и выполнения плана
Темп роста производства продукции отрасли в отчетном году по сравнению с предыдущим (базисным) годом составил 108 %, притом, что прирост производства продукции на отчетный год был запланирован на уровне 5 % по сравнению с предыдущим периодом. Необходимо установить, чему равен процент выполнения отраслевого плана по производству продукции в отчетном году.
Решение
Процент выполнения планового задания в отчетном году определяется по формуле 4.8. В связи с чем, для его расчета, необходимо установить коэффициент выполнения планового задания.
Преобразовав формулу 4.10, получим:
kвып.пл.з = kp / kp.пл.з.
Коэффициент роста производства продукции в отчетном году по сравнению с предыдущим получим, преобразовав формулу 4.2: kp = Tp / 100. Он равен 1,08 (108 : 100).
Коэффициент роста планового задания производства продукции получим, последовательно преобразовав формулы 4.5 и 4.6: kp.пл.з = Tp.пл.з / 100. Tp.пл.з = Tпp.пл.з +100.
Таким образом, темп роста планового задания равен 105 % (5 + 100), а коэффициент роста планового задания 1,05 (105 : 100).
Итак, коэффициент выполнения планового задания по производству продукции в отчетном году равен 1,029 (1,08 : 1,05), а процент выполнения планового задания – 102,9 % (1,029 × 100), т.е. отраслевой план по производству продукции перевыполнен на 2,9 %.
Относительная величина структуры (d) характеризует долю (удельный вес) составляющего элемента в общем итоге совокупности и рассчитывается в форме процента по формуле:
| d = | У | × 100, (4.11) |
| ΣУ |
где У и ΣУ – соответственно уровень части совокупности и суммарный уровень совокупности.
Совокупность относительных величин структуры показывает строение изучаемого явления.
Пример расчета относительных величин структуры
По данным таблицы 4.1 следует охарактеризовать структуру фактических доходов бюджета Республики Крым в 2018 году.
Решение
Решение задачи оформлено с помощью таблицы 4.5.
Таблица 4.5
| Показатель | Сумма, млн. руб. | Расчет по формуле 4.11 | Удельный вес, % |
|---|---|---|---|
| Налоговые доходы | 36246,5 | 36246,5 : 161686,4 × 100 | 22,4 |
| Неналоговые доходы | 4408,0 | 4408,0 : 161686,4 × 100 | 2,7 |
| Безвозмездные поступления | 121031,9 | 121031,9 : 161686,4 × 100 | 74,9 |
| Доходы бюджета Республики Крым, всего | 161686,4 | – | 100,0 |
Таким образом, наибольшую долю доходов бюджета Республики Крым в 2018 году составили безвозмезные поступления в виде дотаций, субсидий, субвенций и иных безвозмезных поступлений (практически 75%). Налоговые поступления составили всего 22,4%, а неналоговые поступления в виде доходов от использования имущества, находящегося в государственной и муниципальной собственности, платежей при использовании природных ресурсов, доходов от продажи активов, штрафов, санкций и т.д. – 2,7%.
Относительная величина координации (ОВК) показывает, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1,10, 100,1000, … единиц другой части и рассчитывается как отношение частей данной совокупности к одной из них, принятой за базу сравнения, по формуле:
| ОВК = | Уi | × 100, (4.12) |
| Уj |
где Уi и Уj – соответственно, уровни i-ой и j-ой частей совокупности.
Относительные величины координации могут рассчитываться как по показателям в абсолютном выражении, так и по относительным величинам структуры.
Пример расчета относительной величины координации
В качестве примера относительной величины координации можно рассматривать показатель, отражающий сумму безвозмездных поступлений, приходящихся на рубль налоговых доходов, рассчитанный по данным таблицы 4.5 по формуле 4.12: ОВКбп/нд = 121031,9 : 36246,5 = 3,34. Это означает, что на каждый рубль налоговых доходов бюджета Республики Крым в рассматриваемом периоде приходилось 3 рубля 34 копейки безвозмездных поступлений.
Относительная величина сравнения (ОВС) характеризует сравнительные размеры одноименных величин (одних и тех же показателей), относящихся к одному и тому же периоду или моменту времени, но к различным объектам или территориям, и рассчитывается как отношение этих величин по формуле:
ОВС = ФА / ФВ, (4.13)
где ФА и ФВ – соответственно, значения показателей, относящихся к одному и тому же периоду или моменту времени, но к объектам (территориям) А и В.
Интерпретация относительных величин сравнения зависит от базы сравнения.
Пример расчета относительной величины сравнения
В качестве примера относительной величины сравнения предлагается показатель, отражающий соотношение расходов консолидированных бюджетов Республики Крым и г. Севастополя в 2018 году, рассчитанный по данным таблицы 4.1 по формуле 4.13: ОВСРК/С = 175470,5 : 35713,5= 4,9. Таким образом, консолидированный бюджет Республики Крым в 2018 году почти в пять раз больше соответственного бюджета г. Севастополь.
Относительная величина интенсивности (ОВИ) характеризует насыщенность изучаемым явлением определенной среды, т.е. степень распространения или уровень развития соответствующего явления в той или иной среде.
Относительные величины интенсивности представляют собой соотношение уровней разноименных, но связанных между собой, показателей и показывают, сколько единиц одной совокупности приходится на единицу другой совокупности. Они рассчитываются по формуле:
ОВИ = ЯХ / СЯХ, (4.14)
где ЯХ – уровень показателя, характеризующего явление Х;
СЯХ – уровень показателя, характеризующего среду распространения явления Х.
Пример расчета относительной величины интенсивности
По данным таблицы 4.1 можно рассчитать валовой региональный продукт Республики Крым на душу населения за 2017 или 2018 год, адаптировав формулу 4.14 к конкретным показателям (табл. 4.6).
Таблица 4.6
| Показатели | 2017 г. | 2018 г. |
|---|---|---|
| Среднегодовая численность населения Республики Крым (ЧН), тыс. чел. | 1912,9 | 1913,5 |
| Валовой региональный продукт Республики Крым (ВРП), млн. руб. | 382355,0 | 415880,0 |
| Валовой региональный продукт Республики Крым на душу населения, млн. руб./тыс. чел. | 199,9 | 217,3 |
К примерам относительных величин интенсивности относятся показатели, характеризующие население (коэффициенты рождаемости и смертности, естественного и механического прироста, показатели потребления продуктов питания на душу населения, обеспеченности населения жильем и т.п.); показатели, характеризующие эффективность использования факторов производства (производительность труда, фондоотдача, коэффициент оборачиваемости, рентабельности и т.д.) и многие другие социально-экономические показатели.
Средние величины. Свойства средней арифметической величины
Абсолютная величина, характеризующая уровень значения признака отдельной единицы совокупности, не позволяет сравнивать значения аналогичных признаков у единиц, относящихся к разным совокупностям. Сравнивать можно лишь средние показатели.
Средняя величина – это обобщающий показатель, характеризующий типичный уровень явления. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.
Средняя величина показывает уровень признака, отнесенный к единице совокупности, например, средняя заработная плата работников отрасли.
Метод средних величин является одним из основных статистических методов.
Главным условием правильного научного использования средних величин в статистике является соблюдение общих принципов расчета средних величин, таких как:
а) при определении средней величины в каждом конкретном случае нужно исходить из качественного содержания усредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета исходные данные;
б) средняя величина должна, прежде всего, рассчитываться по однородной совокупности.
Качественно однородные совокупности позволяет получить метод группировок, который всегда предполагает расчет системы обобщающих показателей;
в) общие средние должны подкрепляться групповыми средними величинами, ибо динамика групповых средних более полно отражает закономерности развития явления, а динамика общей средней показывает лишь общий результат.
Средние величины делятся на два больших класса: степенные средние и структурные средние, представленные на рис. 4.2.
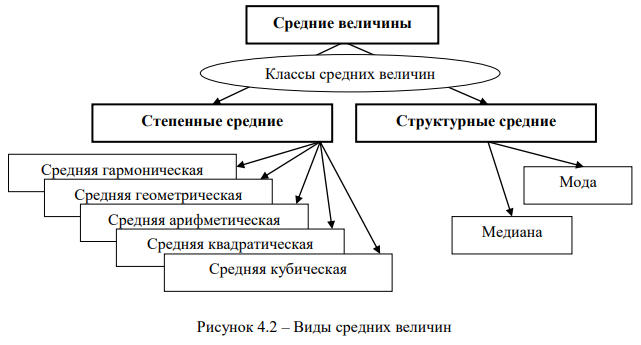
К степенным средним относятся средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая и средняя кубическая величины.
К структурным средним величинам относятся мода и медиана.
Степенные средние величины в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Простая средняя рассчитывается по несгруппированным данным и в общем виде представлена формулой:
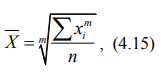
где хi – значение усредняемого признака;
m – показатель степени средней;
n – число вариант (число единиц исследуемой совокупности, равное N).
Взвешенная средняя рассчитывается по сгруппированным данным и в общем виде представлена формулой:
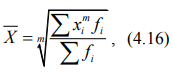
где хi – значение усредняемого признака или серединное значение интервала, в котором оно находися;
m – показатель степени средней;
fi – частота (вес), показывающая, сколько раз встречается i-е значение усредняемого признака.
Веса в формулах средних показывают повторяемость данного значения признака.
Пример расчета средних величин по несгруппированным и сгруппированным данным
Данные для расчета среднего возраста студентов в группе из 20 человек приведены в таблице 4.7.
Таблица 4.7
| № п \ п | Возраст |
|---|---|
| 1 | 18 |
| 2 | 18 |
| 3 | 19 |
| 4 | 20 |
| 5 | 19 |
| 6 | 20 |
| 7 | 19 |
| 8 | 19 |
| 9 | 19 |
| 10 | 20 |
| 11 | 22 |
| 12 | 19 |
| 13 | 19 |
| 14 | 20 |
| 15 | 20 |
| 16 | 21 |
| 17 | 19 |
| 18 | 19 |
| 19 | 19 |
| 20 | 19 |
Средний возраст студентов, рассчитанный по несгруппированным данным, т.е. с использованием методики расчета простой средней величины, равен: (18 + 18 + 19 + 20 + 19 + 20 +...+ 21 + 19 + 19 + 19 + 19) / 20 = 388 / 20 = 19,4 года.
Так как в группе встречаются студенты одного возраста, целесообразно их распределить в группы по возрастному признаку, получив ряд распределения, представленный в таблице 4.8.
Таблица 4.8
| Возраст, лет | 18 | 19 | 20 | 21 | 22 | Всего |
| Число студентов, чел. | 2 | 11 | 5 | 1 | 1 | 20 |
В результате группировки получили новый показатель – частоту, указывающую число студентов определенного возраста. Теперь средний возраст студентов группы можно рассчитать по формуле взвешенной средней: (18 × 2 + 19 × 11 + 20 × 5 + 21 × 1 + 22 × 1) / 20 = 388 / 20 = 19,4 года.
Методики расчета степенных средних величин приведены в таблице 4.9.
Если рассчитать все виды степенных средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних величин: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
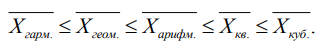
На выбор средней величины влияют содержательные характеристики исходных данных. Так, виды средних величин различаются, прежде всего, тем, какой параметр исходной варьирующей массы индивидуальных значений признака единиц совокупности должен быть сохранен неизменным при его расчете, как на основании фактических данных, так и по усредненным значениям.
Необходимо, чтобы все этапы расчета средней величины имели реальное содержательное обоснование.

Средняя гармоническая величина применяется в тех случаях, когда исходные данные для усреднения значений признака не содержат частот по отдельным значениям признака исследуемой совокупности, а представлены произведением значения признака на частоту (xi×fi = Fi).
Если Fi для всех единиц совокупности будут одинаковы, то применяется формула средней гармонической простой.
Пример расчета средней гармонической величины простой
Ателье по пошиву легкого платья имеет трех закройщиков. Первый закройщик затрачивает на раскрой одного платья в среднем 50 мин, второй – 45 мин, а третий – 40 мин. Необходимо определить среднее время, затрачиваемое на раскрой одного платья в ателье. Время работы каждого работника в течение рабочего дня одинаково и равно 8 × 60 = 480 мин.
Решение
Естественное желание сложить эти три величины и разделить на три (45 мин) было бы оправданным, если бы каждый закройщик за день раскроил только по одному платью. На самом деле в течение восьми часового рабочего дня закройщиками было раскроено разное количество платьев. Число платьев, раскроенных каждым специалистом за рабочий день, можно определить, разделив время, затраченное им в течение рабочего дня на раскрой всех платьев (продолжительность рабочего дня), на среднее время раскроя одного платья.
Среднее время, затрачиваемое на раскрой одного платья в ателье, может быть получено в результате соотнесения всего времени, затраченного на свою работу раскройщиками ателье, к общему числу раскроенных ими платьев.
Отсюда, 44,6 мин.
В результате несложных преобразований пришли к формуле средней гармонической простой (4.17). В приведенном расчете число 3 соответствует числу раскройщиков ателье (n), 8 – продолжительность рабочего дня в часах, 60 – продолжительность часа в минутах (Fi = 8 × 60), 50, 45 и 40 – среднее время в минутах раскроя одного платья отдельными закройщиками (xi).
К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по нескольким предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали и т.п., при условии, что общие затраты соответствующих ресурсов у рассматриваемых единиц совокупности будут одинаковыми.
Средняя гармоническая простая в статистических расчетах встречается редко, в отличие от средней гармонической взвешенной.
Пример расчета средней гармонической величины взвешенной
Общие годовые затраты на производство кондитерских изделий (тортов) и себестоимость единицы продукции по трем кондитерским фабрикам представлены в таблице 4.10. Необходимо рассчитать среднюю себестоимость торта по трем кондитерским фабрикам.
Таблица 4.10
| Номер кондитерской фабрики | Общие издержки производства тортов, тыс. руб. | Себестоимость изготовления одного торта, руб. |
|---|---|---|
| 1 | 2000 | 205 |
| 2 | 4600 | 236 |
| 3 | 1100 | 220 |
Решение
Себестоимость изготовления единицы продукции определяется соотношением общих затрат на выпуск всей продукции с количеством выпущенной продукции. Так как количество продукции показывает как часто встречается та или иная себестоимость единицы продукции, то именно оно выступает частотой ( fi). Затраты на изготовление единицы продукции (себестоимость) являются усредняемым признаком (xi). Общие затраты на производство продукции есть не что иное как xi × if = If. Таким образом, для расчета средней себестоимости торта по трем кондитерским фабрикам применяется формула средней гармонической взвешенной (4.18) и, соответственно, 224,84 руб.
Средняя геометрическая величина применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной, т.е. определяется не суммированием, а умножением индивидуальных значений признака.
В статистических исследованиях развития социально-экономических явлений средняя геометрическая применяется при анализе рядов динамики, в частности, при определении среднего коэффициента роста, когда задана последовательность соответствующих относительных величин динамики. Методика расчета средних относительных величин динамики и соответствующие примеры рассмотрены в теме 9.
Кроме того, средняя геометрическая величина дает наиболее правильный по содержанию результат усреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.
Пример расчета средней геометрической величины простой
Максимальный размер выигрыша в лотерее составляет 1 млн. руб., а минимальный – 100 руб. Какова величина среднего выигрыша? Если сложить эти две величины и разделить пополам, то получим 500050 руб., а это, как и миллион, крупный, и никак не средний, выигрыш; он качественно однороден с максимальным выигрышем и резко отличен от минимального. Расчет по формуле средней гармонической дает среднюю величину в 199,98 руб., что слишком близко к минимальному значению. Только геометрическая средняя величина дает верный с точки зрения экономической логики ответ: 10000 руб. Десять тысяч, действительно, нечто среднее между сотней и миллионом.
Средняя геометрическая величина взвешенная в практических расчетах не применяется.
Средняя арифметическая является наиболее распространенным видом степенных средних.
Средняя арифметическая величина используется в случаях, когда объем усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом, если индивидуальные значения признака у единиц совокупности заменить средней арифметической величиной, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая величина это среднее слагаемое. Примеры расчета простой и взвешенной средних арифметических рассмотрены ранее, по данным таблицы 4.7 (с. 57).
Средняя арифметическая величина обладает рядом свойств:
– первое свойство: сумма отклонений индивидуальных значений признака от его среднего значения равна нулю:
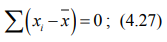
– второе свойство: если каждое индивидуальное значение признака умножить или разделить на постоянное число с, то и средняя величина увеличится или уменьшится во столько же раз:
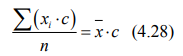
или
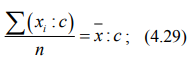
Вследствие этого свойства индивидуальные значения признака можно сократить в с раз, произвести расчет средней величины и результат умножить на с.
– третье свойство: если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число с, то средняя величина возрастет или уменьшится на это же число:
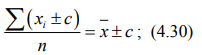
– четвертое свойство: если веса средней взвешенной величины умножить или разделить на постоянное число, средняя величина не изменится. Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерения. Исходя из этого свойства, абсолютные значения весов можно заменить их процентным выражением, приняв Σf = 100;
– пятое свойство: сумма квадратов отклонений индивидуальных значений признака от средней арифметической величины меньше, чем от любого другого числа.
Первое и пятое свойства положены в основание изучения вариации признаков.
Прикладные свойства средней арифметической величины можно проиллюстрировать, применив упрощенный способ расчета значений усредняемого признака, называемый «методом моментов», или способом отсчета от условного начала. Как правило, этот метод применяется для расчета средней арифметической величины по данным интервального вариационного ряда, если варианты и веса имеют большие значения.
Средняя арифметическая величина по данным интервального вариационного ряда (характеристика интервального вариационного ряда представлена в теме 5) рассчитывается по формуле:
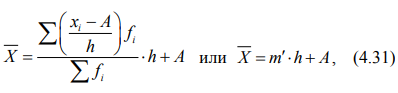
где А – середина одного из центральных интервалов, имеющего, как правило, наибольший вес;
h – величина интервала;
m' – момент первого порядка, рассчитываемый по формуле:
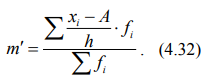
Когда при группировке значения усредняемого признака заданы интервалами, тогда при расчете средней арифметической величины в качестве значения признака в группах применяются середины этих интервалов. Для открытых интервалов в первой и в последней группе, если таковые имеются, значения признака целесообразно определять экспертным путем исходя из сущности свойств признака единицы совокупности. Например, по данным таблицы 4.11 можно минимальный возраст рабочих считать 17 лет, а максимальный возраст – 65 лет. Тогда первый интервал будет от 17 до 20 лет, а последний интервал – 50-65 лет. При отсутствии возможности обосновать четкие границы совокупности, для определения середины открытого интервала исходят из того, что ширина открытого интервала принимается равной ширине смежного с ним интервала, как показано в таблице 4.12.
Таблица 4.11
| Группы рабочих, сформированные по возрасту, лет | Середина интервала |
|---|---|
| До 20 | 18,5 |
| 20-30 | 25 |
| 30-40 | 35 |
| 40-50 | 45 |
| Старше 50 | 57,5 |
Таблица 4.12
| Группы предприятий, сформированные по численности работающих, чел. | Середина интервала |
|---|---|
| До 100 | 50 |
| 100-200 | 150 |
| 200-300 | 250 |
| 300-400 | 350 |
| 400 и выше | 450 |
Пример расчета средней арифметической взвешенной методом моментов
В таблице 4.13 приведены сведения о заработной плате работников предприятия (данные условные). Необходимо рассчитать средний уровень заработной платы персонала предприятия.
Решение
Для оформления решения многих задач в статистике целесообразно использовать таблицы, позволяющие сократить время решения, сэкономить место и наглядно показать последовательность выполняемых действий, путем формирования соответствующих столбцов или строк, следующих один за другим по ходу выполняемых действий.
Для сравнения эту задачу будем решать по формуле средней арифметической взвешенной (формула 4.22) и методом моментов (формула 4.31).
Таблица 4.13
| Группы работников по уровню заработной платы, руб. | Число работников, чел. |
|---|---|
| 8000-10000 | 20 |
| 10000-12000 | 80 |
| 12000-14000 | 160 |
| 14000-16000 | 90 |
| 16000-18000 | 40 |
| 18000 и выше | 10 |
| Всего | 400 |
Результаты промежуточных расчетов для определения средней заработной платы работников предприятия по формуле 4.22 приведены в таблице 4.14.
Таблица 4.14
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | xi × fi |
|---|---|---|---|
| 8000-10000 | 20 | 9000 | 180000 |
| 10000-12000 | 80 | 11000 | 880000 |
| 12000-14000 | 160 | 13000 | 2080000 |
| 14000-16000 | 90 | 15000 | 1350000 |
| 16000-18000 | 40 | 17000 | 680000 |
| 18000 и выше | 10 | 19000 | 190000 |
| Всего | 400 | - | 5360000 |
Средняя заработная плата работников предприятия: 13400 руб.
Результаты промежуточных расчетов для определения средней заработной платы работников предприятия методом моментов по формуле 4.31 приведены в таблице 4.15.
Таблица 4.15
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | xi – А | (xi – А)/h | (xi – А)/h × f/10 |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 8000-10000 | 20 | 9000 | -4000 | -2 | -4 |
| 10000-12000 | 80 | 11000 | -2000 | -1 | -8 |
| 12000-14000 | 160 | 13000 | 0 | 0 | 0 |
| 14000-16000 | 90 | 15000 | 2000 | 1 | 9 |
| 16000-18000 | 40 | 17000 | 4000 | 2 | 8 |
| 18000 и выше | 10 | 19000 | 6000 | 3 | 3 |
| Всего | 400 | х | х | х | 8 |
Сначала воспользуемся третьим свойством средней арифметической взвешенной, которое позволяет исчислить среднюю величину не по фактическим значениям вариант, а по отклонениям вариант от постоянной А, в качестве которой принято брать серединную варианту ряда с наибольшей частотой. А = 13000 руб., так как этому значению варианты соответствует наибольшая частота – 160 человек.
Найдем отклонения вариант от этой величины и получим значения новых вариант (xi – 13000) (стлб. 4 табл. 4.15).
Далее на основании второго свойства средней арифметической уменьшим варианты в несколько раз. В качестве кратного числа возьмем величину интервала ряда распределения, равную 2000. Разделив значения вариант (xi – 13000) на 2000, получим новые значения вариант
(стлб. 5 табл. 4.15).
Используя четвертое свойство, сократим частоты в 10 раз и умножим полученные значения на варианты: cтлб. 6 табл. 4.15).
В формуле 4.32 преобразуем знаменатель в соответствии с выдвинутым условием деления частот на 10 и с учетом установленных А и h получим m' = 0,2 руб.
Средняя заработная плата работников предприятия, исчисленная по формуле 4.31: 13400 руб.
Ощутить преимущества расчета средних арифметических величин методом моментов можно только при достаточно большом массиве исходных усредняемых данных.
Средней средних арифметических величин является средняя хронологическая величина, рассчитываемая по формуле:
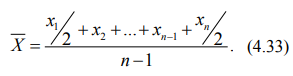
Средняя хронологическая величина используется в том случае, если усредняемые значения признака единиц статистической совокупности заданы на определенный момент времени, т.е. единицы совокупности характеризуются моментными признаками. Пример расчета средней хронологической величины приведен в теме 9.
Средняя квадратическая величина используется, если при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов его исходных значений. Вместе с тем, основной сферой применения методики средней квадратической является измерение степени колеблемости индивидуальных значений признака относительно средней арифметической величины посредством расчета среднего квадратического отклонения.
Пример расчета средней квадратической величины
Имеются три земельных участка со сторонами квадрата: х1 = 100 м; х2 = 200 м; х3 = 300 м.
Необходимо определить среднюю величину стороны участков.
Арифметическая средняя величина (100 + 200 + 300) : 3 = 200 м дает неверный результат, так как общая площадь трех участков со стороной 200 м была бы равна: 3 × 2002 = 120000 м2, в то время как площадь исходных трех участков равна: 1002 + 2002 + 3002 = 140000 м2. Именно эту суммарную площадь участков дает средняя величина, рассчитанная по методике средней квадратической: 216 м.
Если по условию задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, то для расчета средней используют методику определения средней кубической величины.
В статистической практике чаще, чем остальные виды средних взвешенных величин, используются средние арифметические и средние гармонические взвешенные.
В частности, при усреднении относительных величин интенсивности (так называемых, качественных показателей), смысловую основу которых определяет соответствующая логическая формула, эта формула, в зависимости от имеющих исходных данных, может принимать вид средней арифметической или средней гармонической взвешенной величины.
При выборе вида (формулы) средней величины качественного показателя следует придерживаться определенных правил:
а) если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя его логической формулы, а значения числителя не известны, но могут быть найдены как произведение этих показателей, то средняя должна вычисляться по формуле средней арифметической взвешенной;
б) если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя должна вычисляться по формуле средней гармонической взвешенной;
в) в том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя величина вычисляется непосредственно по этой формуле.
Пример применения правила выбора формулы средней величины качественного показателя
При выполнении типологической группировки (табл. 3.4) отмечалось, что среднюю урожайность зерновых культур по группам предприятий и их совокупности в целом рассчитать невозможно из-за отсутствия данных о размерах посевных площадей предприятий. Тем не менее, отталкиваясь от логической формулы урожайности, рассчитаем среднюю урожайность зерновых культур по группам сельскохозяйственных предприятий (государственным предприятиям, обществам с ограниченной ответственностью и фермерским хозяйствам) и совокупности сельхозпредприятий региона в целом.
Урожайность зерновых культур рассчитывается делением суммы валового сбора зерновых культур на величину посевных площадей, с которых снят этот урожай.
Так как валовой сбор известен, а величина посевных площадей – нет, но может быть найдена путем деления валового сбора по конкретному предприятию на урожайность, выращенных им зерновых культур, и суммирования полученных результатов, то для расчета средней урожайности по группе предприятий используется формула средней гармонической взвешенной (правило (б)).
Средняя урожайность зерновых культур государственных предприятий равна: 20,6 ц/га.
Результаты расчетов подтверждают выводы, сделанные по результатам комбинационной группировки в примере к теме 3, относительно того, что урожайность зерновых культур государственных предприятий самая низкая, а фермерских хозяйств – самая высокая.
Для того чтобы показать применение первого (а) и третьего (в) правила выбора формулы средней величины качественного показателя, по результатам расчетов средней урожайности зерновых культур по группам предприятий различных организационно-правовых форм составим таблицу 4.16 с двумя вариантами исходных данных для расчета средней урожайности зерновых культур по всем сельхозяйственным предприятиям региона.
Таблица 4.16
| Группы сельскохозяйственных предприятий по организационно-правовой форме хозяйствования | Вариант 1 | Вариант 2 | ||
|---|---|---|---|---|
| Посевная площадь, га | Средняя урожайность, ц/га | Валовой сбор, ц | Посевная площадь, га | |
| Государственные предприятия | 28227,4 | 20,6 | 580828 | 28227,4 |
| Обшества с ограниченной ответственностью | 41471,1 | 23,3 | 966723,7 | 41471,1 |
| Фермерские хозяйства | 2430,8 | 30,6 | 74275 | 2430,8 |
| Всего | 72129,3 | – | 1621826,7 | 72129,3 |
Первый вариант исходных данных позволяет рассчитать среднюю урожайность зерновых культур по региону по формуле средней арифметической взвешенной (правило (а)), так как известны численные значения знаменателя логической формулы урожайности (посевные площади), а значения числителя (валового сбора) не известны, но могут быть найдены как произведение средней урожайности предприятий соответствующих организационно-правовых форм хозяйствования на размеры их посевных площадей: 22,5 ц/га.
Второй вариант исходных данных позволяет рассчитать среднюю урожайность зерновых культур по региону по логической формуле урожайности (правило (в)), так как известны численные значения и ее числителя (валовой сбор) и ее знаменателя (посевные площади): 22,5 ц/га.
Таким образом, средняя урожайность зерновых культур сельскохозяйственных предприятий региона составила 22,5 ц/га.
