Индексный метод
Понятие о статистических индексах
В переводе с латинского языка слово «индекс» означает «показатель», однако в статистике оно приобретает самостоятельное значение.
Статистический индекс – относительный показатель, отражающий соотношение величин сложного экономического явления, состоящего из соизмеримых или несоизмеримых элементов.
Значительная часть статистических совокупностей, состоит из элементов, которые можно подытожить. Так, для анализа динамики численности рабочих и служащих, занятых в народном хозяйстве страны, всего лишь нужно суммировать соответствующие данные по отдельным отраслям народного хозяйства базисного и отчетного периодов. Соотношение численности всех работников, занятых в народном хозяйстве страны, отчетного и базисного периодов возможно потому, что в основе таких сравнений лежит соизмеримость элементов, из которых складываются сравниваемые совокупности. Однако большинство совокупностей состоит из элементов, непосредственно не суммируемых. Например, с такими совокупностями имеют дело, когда изучают динамику производства продукции или объема товарооборота, которые в натуральной форме складываются из разных потребительских благ и, будучи, выраженными в натурально-вещественной форме, эти элементы не могут непосредственно суммироваться. Нельзя складывать тонны цемента и тонны сахара, или пары обуви и м3 газа и т.д.
Чтобы преодолеть существующую несоизмеримость элементов сложного явления используют соизмеритель, в основе которого лежит то общее, что свойственно всем элементам совокупности независимо от их натурально-вещественной формы. Например, это может быть стоимость продукта, выражаемая ценой. Стоимость разнородной продукции можно складывать, определяя тем самым объем всей продукции, что позволяет рассчитывать обобщающие показатели в виде индексов. Посредством денежного выражения стоимости отдельных видов продукции исчезает (снимается) их несравнимость как потребительных стоимостей.
Перечень задач, решаемых с помощью индексного метода, приведен на рис. 11.1.
С помощью индексного метода решаются следующие задачи:
- получают сравнительную характеристику изменения явления во времени, где индексы выступают как показатели динамики
- характеризуют выполнение установленной нормы, утвержденного стандарта (плана), где индексы выступают как показатели выполнения задания (плана) и являются средством оперативного отражения хода производственного процесса
- дают сравнительную характеристику изменения явления в пространстве, в этом случае индексы обеспечивают территориальное сравнение (территориальные индексы)
- оценивают роль отдельных факторов, формирующих сложное явление
Рисунок 11.1. – Задачи индексного метода
Широкий спектр задач, решаемых с помощью индексного метода, предопределяет формирование и использование целой системы этих показателей, приведенной в таблице 11.1.
Таблица 11.1
| Классификационный признак | Названия индексов | Характеристика индексов |
|---|---|---|
| По характеру исследуемых объектов | Индексы количественных (объемных) показателей | это индексы физического объема продукции, физического объема розничного товарооборота, индексы рабочего времени и др. В них дается характеристика изменения объема того или иного явления |
| Индексы качественных показателей | это индексы цен, себестоимости продукции, производительности труда и фондоотдачи, средней заработной платы и др. С помощью этих индексов дается характеристика изменения качественного признака, который отражает особенности развития явления | |
| По степени охвата единиц совокупности | Индивидуальные индексы | дают сравнительную характеристику отдельных элементов сложного явления |
| Общие индексы | характеризуют изменение совокупности, в которую входят разнородные элементы | |
| В зависимости от методики расчета общих индексов | Агрегатные индексы | основная форма статистических индексов (п. 11.2) |
| Средние из индивидуальных индексов | являются производными индексами, их получают вследствие преобразования агрегатных индексов (п. 11.3) | |
| В зависимости от базы сравнения | Цепные индексы | имеют место, если база сравнения в каждом индексе все время изменяется: принимаются данные предыдущего периода относительно отчетного |
| Базисные индексы | имеют место, если при определении индексов взята постоянная база, например, за первый год исследования | |
| Индексы средних величин | Индексы переменного состава | характеризуют изменение средних величин качественных признаков и отражают изменение собственно индексируемого признака и изменение структуры изучаемого явления |
| Индексы постоянного состава | характеризуют изменение качественного показателя (признака), которое изучается в условиях неизменной структуры совокупности | |
| Индексы структурных сдвигов | характеризуют изменение средних величин качественных признаков только за счет изменение структуры изучаемого явления. Выступают факторами изменения средних значений показателей при изучении влияния сдвигов в структуре весов на изменение индексируемых величин |
Количественные показатели представлены абсолютными величинами, характеризующими объем или уровень развития явления, которые выражаются в определенных (как правило, натуральных, трудовых, демографических) единицах измерения. Качественные показатели, выражены, как правило, относительными величинами интенсивности, и характеризуют уровень изучаемого результативного показателя в расчете на количественную единицу и определяются как отношение данного результативного показателя к связанному с ним количественному показателю, на единицу которого он рассчитывается. Например, себестоимость единицы продукции рассчитывается как отношение суммарных затрат на производство к количеству продукции.
Индивидуальные индексы обозначаются с помощью буквы i. Около основания индекса всегда ставится символ того явления, изменение которого изучают. Показатель, изменение которого изучается, называется индексируемым, и его сопровождают знаком 1, если это данные отчетного периода, и 0, если они представлены за базисный период.
Например, индивидуальный индекс физического объема продукции определенного вида (iq), представленный в форме коэффициента, рассчитывается по формуле:
| iq = | q1 | , (11.1) |
| q0 |
где q0 и q1 – соответственно объем конкретного вида продукции базисного и отчетного периодов в натуральных единицах измерения.
Общие (сводные) индексы обозначаются I. Если индексы охватывают не все единицы совокупности, то такие индексы называют групповыми, или субиндексами.
Выбор формы индекса в зависимости от методологии расчета общих индексов зависит от цели исследования и имеющейся информации.
Индекс как относительная величина может быть выражен в виде коэффициентов или процентов.
Агрегатный индекс как основная форма общего индекса
Агрегатные индексы являются основной формой экономических индексов.
При моделировании агрегатных индексов необходимо придерживаться общепринятого в статистике порядка символического обозначения соответствующих явлений, представленного на рис. 11.2.
- q – количество продукции в натуральных единицах
- p – цена единицы продукции или товара
- z – себестоимость единицы продукции
- t – трудоемкость изготовления единицы продукции
- w – средняя выработка продукции в расчете на одного работника
- Т – средняя численность работников
Рисунок 11.2 – Обозначения показателей, изучаемых с помощью индексов
Для построения общих индексов важно учитывать взаимосвязь приведенных на рис. 11.2 показателей, так:
- pq – стоимость произведенной или реализованной продукции (общий товарооборот);
- zq – общие затраты на производство продукции в денежном выражении;
- tq - общие затраты времени на производство продукции выраженные в трудовых единицах измерения;
- wТ – объем произведенной продукции Q (в натуральном или стоимостном выражении в зависимости от того в каких единицах измерения выражена выработка продукции);
- t = 1/w;
- w = 1/t.
Основная сложность построения общих индексов состоит в преодолении несоизмеримости разных элементов, составляющих совокупность. Одним из возможных способов достижения этого является введение в индекс дополнительного и при этом неизменного показателя, который экономически тесно связан с индексируемой величиной, называемого, как отмечалось в п. 11.1, соизмерителем. Например, для количества продукции таким соизмерителем может быть как цена, так и себестоимость или трудоемкость единицы продукции. Умножив объем каждого вида продукции на соответствующий ему соизмеритель получают показатели, которые можно не только подытожить, но и сопоставить полученные суммы между собой.
Механизм построения общих индексов рассмотрим на примере показателей физического объема реализации отдельных видов продукции (q), их цен (p) и товарооборота (qp).
Сумма произведений количества продукции на его соизмериталь (цену) приводит к образованию объединений или агрегатов Σqp («aggrego» – в переводе с латинского – присоединяю). Построенный на их основе общий индекс, в числителе и в знаменателе которого суммы произведений уровней признаков, получил название агрегатного индекса. Эта форма индекса более 100 лет назад была разработана немецкими статистиками Э. Леспейресом (1874 г.) и Г. Пааше (1864 г.).
Перемножение агрегируемых признаков, позволяет не только решить проблему сопоставимости, а и учесть веса соизмерителей в реальных экономических процессах. Так, если индексируемой величиной является качественный признак, то в общем индексе его уровень умножается на значения связанного с ним количественного показателя, который играет роль веса.
Для определения изменения стоимости реализованной продукции в текущем периоде по сравнению с базисным используется общий индекс, называемый в статистике индексом товарооборота (Ipq), рассчитываемый по формуле:
| Ipq = | Σp1q1 | , (11.2) |
| Σp0q0 |
где p1q1, p0q0 – товарооборот отдельных видов товаров соответственно в отчетном и базисном периодах.
Приведенный индекс характеризует изменение сложного явления – товарооборота под влиянием таких факторов: изменения физического объема продажи отдельных товаров и изменения цен, по которым они реализовывались. Чтобы изучить влияние одного из этих факторов на изменение товарооборота, следует другой принять условно неизменным, т.е. зафиксировать его на уровне определенного периода.
В отечественной статистической практике принят следующий порядок фиксирования созмерителей (весов):
- при построении индексов качественного признака его веса фиксируются на уровне отчетного периода;
- при построении индексов количественных (объемных) признаков – признаки-соизмерители фиксируются на уровне базисного периода.
Этот принцип обеспечивает возможность построения системы взаимозависимых индексов.
Как изменился товарооборот только за счет изменения количества проданных товаров в отчетном периоде по сравнению с базисным периодом, позволяет оценить общий индекс физического объема товарооборота (Iq), рассчитываемый по формуле:
| Iq = | Σp0q1 | , (11.3) |
| Σp0q0 |
Принимая цены на уровне базисного периода при построении индексов физического объема, полностью устраняется влияние цен на величину индекса.
Как изменился товарооборот только за счет изменения цен проданных товаров в отчетном периоде по сравнению с базисным периодом, позволяет оценить общий индекс цен (Ip), рассчитываемый по формуле:
| Ip = | Σp1q1 | , (11.4) |
| Σp0q1 |
При условии фиксирования количества проданных товаров на уровне отчетного периода открывается возможность определить реальную экономию, которую получит население в случае снижения цен, или дополнительные затраты, если цены растут.
Аналогичным образом (формулы 11.2-11.4) строятся агрегатные индексы других показателей.
Пример расчета индивидуальных и агрегатных индексов
По данным таблицы 11.2 следует проанализировать динамику физического объема продаж, цен и выручки от реализации (товарооборота) как отдельных видов товаров, так и всей выделенной товарной группы бакалейных изделий в розничной торговле города N в 2019 г. по сравнению с 2018 г.
Решение
Для изучения динамики физического объема продаж и цен отдельных продуктов бакалейной группы в розничной торговле города N в 2019 г. по сравнению с 2018 г., а также выручки от их реализации, рассчитаем индивидуальные индексы физического объема, цен и товарооборота в соответствии с методикой, представленной формулой 11.1.
Стоимость продаж (выручка от реализации) каждого вида товаров определяется как произведение физического объема его реализации на цену. Результаты расчетов соответствующих показателей приведены в таблице 11.3.
Таблица 11.2
| Наименование товара | Продано товаров, т | Средняя цена за 1 кг, руб. 1) | ||
|---|---|---|---|---|
| 2018 г. | 2019 г. | 2018 г. | 2019 г. | |
| Сахар-песок | 1360 | 1324 | 47,19 | 31,78 |
| Крупа гречневая-ядрица | 1050 | 920 | 37,12 | 61,66 |
| Вермишель | 1240 | 1280 | 64,68 | 67,53 |
| Чай черный байховый | 158 | 142 | 765,56 | 834,71 |
| Кофе натуральный растворимый | 726 | 730 | 2393,6 | 2400,85 |
Примечание: 1) фактические средние цены по Республике Крым за декабрь 2018 г. и 2019 г. [29].
Таблица 11.3
| Наименование товара | Продано товаров, т | Средняя цена за 1 кг, руб. | Стоимость проданных товаров, млн. руб. | Индивидуальные индексы, % | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2018г. | 2019г. | 2018г. | 2019г. | 2018г. | 2019г. | 2019г. в ценах 2018г. | физического объема | цен | стоимости продаж | |
| q0 | q1 | p0 | p1 | p0q0 | p1q1 | q1p0 | iq | ip | iqp | |
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Сахар-песок | 1360 | 1384 | 47,19 | 31,78 | 64,2 | 44,0 | 65,3 | 101,8 | 67,3 | 68,5 |
| Крупа гречневая ядрица | 1050 | 920 | 37,12 | 61,66 | 39,0 | 56,7 | 34,2 | 87,6 | 166,1 | 145,4 |
| Вермишель | 1240 | 1280 | 64,68 | 67,53 | 80,2 | 86,4 | 82,8 | 103,2 | 104,4 | 107,7 |
| Чай черный байховый | 158 | 142 | 765,56 | 834,71 | 121,0 | 118,5 | 108,7 | 89,9 | 109,0 | 97,9 |
| Кофе натуральный растворимый | 726 | 730 | 2393,60 | 2400,85 | 1737,8 | 1752,6 | 1747,3 | 100,6 | 100,3 | 100,9 |
| Всего | х | х | х | х | 2042,2 | 2058,2 | 2038,3 | х | х | х |
Данные столбца 8 таблицы 11.3 свидетельствуют о том, что в 2019 г. по сравнению с 2018 г. физический объем продаж сахара-песка, вермишели и кофе натурального растворимого увеличился соответственно на 1,8% (101,8 – 100,0), 3,2% (103,2 – 100,0) и 0,6% (100,6 –100,0). В то же время, в анализируемом периоде отмечается уменьшение физического объема продаж гречневой крупы на 12,4% (87,6 – 100,0) и чая черного байхового на 10,1% (89,9 – 100,0).
По данным столбца 9 таблицы 11.3 видно, что цены практически на все виды товаров в исследуемом периоде увеличились, в частности: на крупу гречневую-ядрицу на 66,1%; на вермишель на 4,4%; на чай черный байховый на 9,3%; на кофе натуральный растворимый на 0,3 %. Исключение составили только цены на сахар, уменьшившиеся в 2019 г. по сравнению с 2018 г. на 32,7% (67,3 – 100,0).
Соответствующая динамика физического объема продаж и цен отдельных видов бакалейной продукции обусловила рост выручки от реализации в розничной торговле города N в 2019 г. по сравнению с 2018 г. крупы гречневой-ядрицы на 45,4%, вермишели на 7,7% и кофе натурального растворимого на 0,9%, и снижение стоимости проданного сахара-песка на 31,5% и чая черного байхового на 2,1% в розничной торговле города N (по данным столбца 10 таблицы 11.3).
Для характеристики динамики физического объема продаж, цен на продукты питания и товарооборота в целом по бакалейному отделу магазина в 2013 г. по сравнению с 2012 г. исчислим соответствующие общие индексы.
Общий индекс физического объема товарооборота выделенной бакалейной продукции, рассчитанный по формуле 11.3 на основе итоговых данных 7 и 5 столбцов таблицы 11.3, равен: Iq = 99,8%, что свидетельствует о снижении общего физического объема ее продаж в 2019 г. по сравнению с 2018 г. на 0,2% (99,8 – 100).
Общий индекс цен, рассчитанный по формуле 11.4 на основе итоговых данных 6 и 7 столбцов таблицы 11.3, равен: Ip = 101,0%, т.е. в 2019 г. по сравнению с 2018 г. цены на выделенную бакалейную продукцию в розничной торговле города N выросли, в общем, на 1,0 % (101,0 – 100).
Общий индекс товарооборота, рассчитанный по формуле 11.2 на основе итоговых данных 5 и 6 столбцов таблицы 11.3, равен: Iqр = 100,8%, что свидетельствует о росте объема товарооборота выделенной бакалейной продукции в розничной торговле города N в 2019 г. по сравнению с 2018 г. на 0,8%.
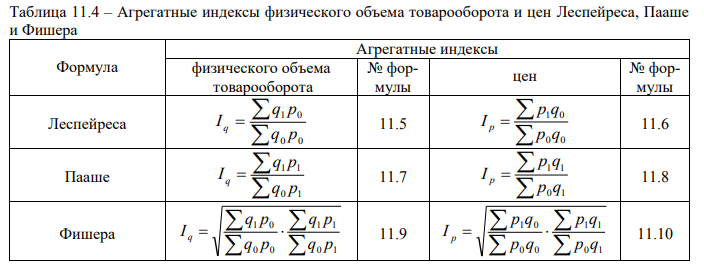
При построении агрегатных индексов физического объема товарооборота и цен в формулах Леспейреса соизмерители (веса) фиксируются на уровне базисного периода, а в формулах Пааше – на уровне отчетного периода, как показано в таблице 11.4. Средняя геометрическая из двух агрегатных индексов (Леспейреса и Пааше) дает «идеальные формулы Фишера» агрегатных индексов физического объема товарооборота и цен.
Общие индексы как средние из индивидуальных индексов
Для определения агрегатных индексов необходимо иметь абсолютные значения индексируемой величины и величины, с помощью которой достигается сравнимость уровней явлений, отдельные элементы которых непосредственно не подытоживаются, т.е. весов индексов и их соизмерителей. Вместе с тем не всегда такие показатели имеются в отчетности, что не позволяет получить некоторые условные показатели необходимые для расчета общих индексов в агрегатной форме, например, сумму товарооборота Σq1p0. При невозможности найти Σq1p0 общие индексы рассчитывают в виде средних из индивидуальных.
Средние из индивидуальных индексов являются производными индексами, их получают вследствие преобразования агрегатных индексов. Поэтому средний из индивидуальных индексов тождественен агрегатному индексу.
Каждый агрегатный индекс может быть преобразован в средний индекс: средний арифметический или средний гармонический.
Средний арифметический индекс целесообразно использовать тогда, когда в агрегатном индексе реальная величина (товарооборот – Σp1q1 или Σp0q0) находится в знаменателе дроби, а средний гармонический индекс целесообразно использовать тогда, когда в агрегатном индексе реальная величина находится в числителе дроби.
Так как в агрегатной форме общего индекса физического объема товарооборота знаменатель формулы 11.3 является величиной реальной, а числитель – условной, то общий индекс физического объема товарооборота будет представлен в виде средней арифметической величины из индивидуальных индексов физического объема товаров (iq), которые взвешены по стоимости продукции базисного периода в базисных ценах (p0q0).
Общий индекс физического объема как средний из индивидуальных индексов рассчитывается по формуле:

В агрегатной форме индекса цен числитель формулы 11.4 является величиной реальной, а знаменатель – условной, поэтому общий индекс цен – это средняя гармоническая величина индивидуальных индексов цен (iр), взвешенных на сумму фактического товарооборота отчетного периода (p1q1).
Общий индекс цен как средний из индивидуальных индексов рассчитывается по формуле:

Индивидуальные индексы в формулах 11.11 и 11.12 выражены в форме коэффициентов.
Как отмечалось, выбор формы индекса (агрегатный или средний из индивидуальных) зависит от цели исследования и имеющейся информации.
Пример расчета общих индексов как средних из индивидуальных индексов
Предположим, что о розничной торговле бакаленой продукцией, рассмотренной в предыдущем примере, имеется информация только об общем объеме товарооборота за 2018 и 2019 годах, а также известна динамика количества каждого вида проданных товаров и их цен (таблица 11.5).
Необходимо установить каким образом на товарооборот бакалейного отдела повлияло в целом изменение физического объема реализованных продуктов и цен на них.
Таблица 11.5
| Наименование товара | Стоимость проданных товаров, млн. руб. | Индивидуальные индексы, % | ||
|---|---|---|---|---|
| 2012 г. | 2013 г. | физического объема | цен | |
| p0q0 | p1q1 | iq | ip | |
| Сахар-песок | 64,2 | 44,0 | 101,8 | 67,3 |
| Крупа гречневая-ядрица | 39,0 | 56,7 | 87,6 | 166,1 |
| Вермишель | 80,2 | 86,4 | 103,2 | 104,4 |
| Чай черный байховый | 121,0 | 118,5 | 89,9 | 109,0 |
| Кофе натуральный растворимый | 1737,8 | 1752,6 | 100,5 | 100,3 |
| Всего | 2042,2 | 2058,2 | х | х |
Решение
Общий индекс физического объема товарооборота бакалейного отдела, рассчитанный по формуле 11.11, равен: Iq = 0,998 или 99,8%, т.е. количество проданных выделенных товаров в 2019 г. по сравнению с 2018 г. уменьшилось на 0,02 %.
Общий индекс цен продукции бакалейного отдела, рассчитанный по формуле 11.12, равен: Ip = 101,0%, что означает средний рост цен на выделенные продукты, реализуемые в розничной торговле города N, в 2019 г. по сравнению с 2018 г. на 1,0%.
Результаты этих расчетов совпадают с данными, полученными при решении предыдущей задачи при расчете общих индексов в агрегатной форме.
Системы взаимосвязанных индексов
Индексный метод широко используется для анализа роли отдельных факторов в динамике сложного экономического явления, изменение которого обусловлено действием нескольких факторов, выступающих сомножителями. Выявление и количественная оценка влияния отдельных факторов на изменение сложного явления – одна из важных задач, стоящих перед индексным методом.
Как отмечалось, динамика товарооборота зависит от динамики физической массы реализуемых товаров и уровня цен на них. Связь между изменением объема товарооборота, выступающего в качестве результативного показателя, количеством проданных товаров и уровнем их цен, являющихся факторными показателями, находит отражение в системе взаимосвязанных индексов товарооборота, представленной формулой:
Iqp = Iq×Ip. (11.13)
Подобные модели – не что иное, как факторные модели типа Х = a×b, где Х – результативный признак, a и b – показатели-факторы. В таких системах считается, что все другие причины изменения результативного признака в той или иной мере учтены в выделенных факторах, а построенная модель адекватна экономическому содержанию изучаемого явления. Количество факторов, включаемых в систему, определяют ее как двухфакторную, трехфакторную или многофакторную модель.
Важно помнить, что как связаны между собой результативный показатель и факторы, так же связаны между собой и соответствующие индексы: IХ = Ia × Ib.
Индексы Ia и Ib являются субиндексами индекса IХ.
Для того чтобы сформировать систему общих индексов, т.е., чтобы произведение двух взаимосвязанных индексов давало итоговый показатель динамики, следует соизмерители (веса) в индексах брать на уровнях разных периодов (п. 11.2).
Безусловным преимуществом индексных систем является возможность их использования для определения не только относительных показателей влияния отдельных факторов на результативный признак, а и возможность определить на их основе абсолютные величины изменения результативного признака в результате действия указанных факторов.
Абсолютный прирост результативного признака раскладывается настолько же частей, на сколько факторов-сомножителей раскладывается сам результативный признак.
Абсолютный прирост результативного признака за счет конкретного фактора рассчитывается как разница между числителем и знаменателем субиндекса этого фактора.
Так, абсолютный прирост товарооборота за счет изменения физического объема реализованной продукции (Δpq(q)) определяется по формуле:
Δpq(q) = Σq1p0 - Σq0p0, (11.14)
а абсолютный прирост товарооборота за счет изменения цен реализованных товаров (Δpq(р)) рассчитывается по формуле:
Δpq(p) = Σp1q1 - Σp0q1. (11.15)
Абсолютный прирост товарооборота (Δpq), исчисленный по формуле
Δpq = Σp1q1 - Σp0q0, (11.16)
равен сумме абсолютных приростов товарооборота, обусловленных влиянием рассмотренных факторов, что может быть выражено формулой:
Δpq = Δpq(q) + Δpq(p). (11.17)
Индексный метод позволяет найти абсолютный прирост товарооборота на основе данных о товарообороте базисного периода и значений общих индексов физического объема товарооборота и цен.
Так, абсолютный прирост товарооборота за счет изменения физического объема реализованной продукции (Δpq(q)) можно найти по формуле:
Δpq(q) = p0q0×(Iq-1), (11.18)
а абсолютный прирост товарооборота за счет изменения цен реализованных товаров (Δpq(р)) по формуле:
Δpq(p) = p0q0×Iq×(Ip-1), (11.19)
Индексную систему часто используют для определения третьего показателя, если известны два других, входящих в систему.
Пример взаимосвязи индексов и расчета величины абсолютного прироста результативного признака за счет изменения признаков-факторов
По результатам решения задачи, рассмотренной в качестве примера в п. 11.2 (с. 186-187),
необходимо показать взаимосвязь общих индексов товарооборота, физического объема товарооборота и цен. Кроме того, следует оценить уровень абсолютного влияния на изменение общего товарооборота выделенных продуктов бакалейной группы, реализованных в розничной торговле города N, изменения физического объема продаж этих продуктов питания и цен на них в 2019 г. по сравнению с 2018 г.
Решение
Справедливость формулы 11.13 подтверждается тем, что выполняется следующее равенство (индексы представлены в форме коэффициентов): 1,008 = 0,998 × 1,01 = 1,008, где 1,008 – это Iqp, 0,998 – Iq, 1,01 – Ip.
Абсолютный прирост товарооборота выделенных продуктов бакалейной группы, реализованных в розничной торговле города N, в 2019 г. по сравнению с 2018 г., рассчитанный по формуле 11.16, составил: Δpq = 2058,2 - 2042,2 = 16,0 млн. руб.
На изменение общего товарооборота повлияло как изменение физического объема продаж выделенных продуктов, так и изменение цен на них.
Увеличение общей выручки от реализации выделенных продуктов в 2019 г. по сравнению с 2018 г. за счет изменения количества тонн проданных товаров, составило Δpq(q) = 2038,3 - 2042,2 = -3,9 млн. руб. (формула 11.14), а за счет изменения цен на продукты питания – Δpq(p) = 2058,2 - 2038,3 = 19,9 млн. руб. (формула 11.15).
Это означает, что уменьшение количества продуктов бакалейной группы, реализованных в розничной торговле города N, в 2019 г. по сравнению с 2018 г. (при условии сохранения цен базисного периода) привело бы к снижению их общего товарооборота на 3,9 млн. руб.
В свою очередь, рост цен на продукты питания в рассматриваемом периоде обусловил увеличение выручки от продаж в розничной сети города N на 19,9 млн. руб., а покупатели в 2019 г. заплатали за выделенные товары на 19,9 млн. руб. больше, чем они это сделали бы в 2018 г. за тот же продуктовый набор.
Правильность проведенных расчетов подтверждает равенство 16,0 = – 3,9 + 19,9 = 16,0 (млн. руб.) (формула 11.17).
Абсолютный прирост товарооборота за счет изменения физического объема реализованной продукции, рассчитанный по формуле 11.18, равен Δpq(q) = 2042,2 × (0,998 – 1) = -4,0 млн. руб., а абсолютный прирост товарооборота за счет изменения цен на товары, рассчитанный по формуле 11.19, равен Δpq(р) = 2042,2 × 0,998 × (1,01 – 1) = 20,4 млн. руб. Несовпадение полученных значений показателей с результатами расчетов по формулам 11.14 и 11.15 обусловлено тем, что в расчетах использовались округленные данные.
Индексы с постоянной и переменной базой сравнения
При изучении динамики показателей, характеризующих социально-экономические явления, возникает необходимость определить индексы за более чем два периода. В таких случаях индексы могут рассчитываться как на основе постоянной, так и переменной баз сравнения (п. 9.2, с. 154).
Если сравнивают количественные характеристики явления, относящиеся к различным периодам времени, с состоянием того же явления в какой-то определенный (как правило, начальный в ряду динамики) период, то получают систему индексов с постоянной базой сравнения – базисные индексы.
Если оценивают относительные изменения уровня изучаемого явления по сравнению с предшествующим периодом, то получают систему индексов с переменной базой сравнения – цепные индексы.
Особенности расчета индивидуальных и общих индексов количественных и качественных показателей с постоянной и переменной базой сравнения рассмотрим на примере базисных и цепных индексов физического объема, цен и товарооборота.
Индивидуальные базисные индексы физического объема рассчитываются по формулам:
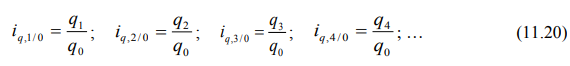
Индивидуальные цепные индексы физического объема рассчитываются по формулам:
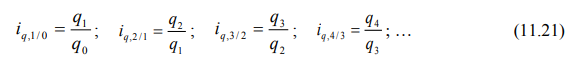
Агрегатные базисные индексы физического объема рассчитываются по формулам:
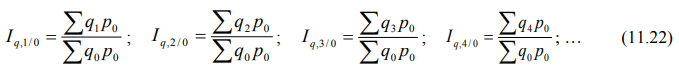
Агрегатные цепные индексы физического объема рассчитываются по формулам:
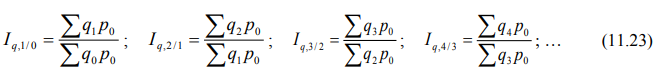
Индивидуальные базисные индексы цен рассчитываются по формулам:
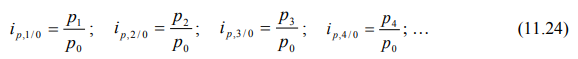
Индивидуальные цепные индексы цен рассчитываются по формулам:
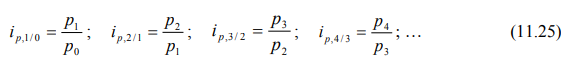
Агрегатные базисные индексы цен рассчитываются по формулам:
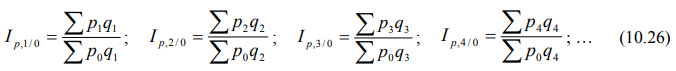
Агрегатные цепные индексы цен рассчитываются по формулам:
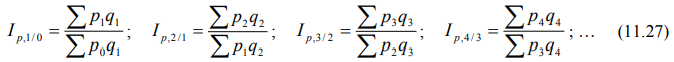
Индивидуальные базисные индексы товарооборота рассчитываются по формулам:
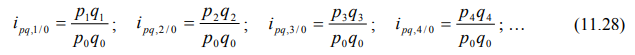
Индивидуальные цепные индексы товарооборота рассчитываются по формулам:
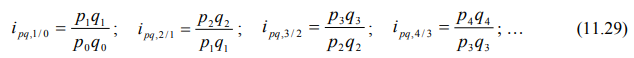
Агрегатные базисные индексы товарооборота рассчитываются по формулам:
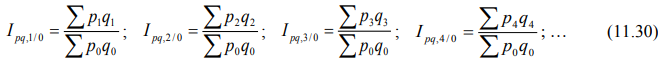
Агрегатные цепные индексы товарооборота рассчитываются по формулам:
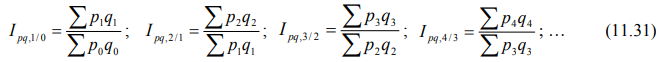
Для индивидуальных индексов цен, физического объема и индексов стоимости продукции справедливо правило (состоящее из двух частей):
1) произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода, т.е. выполняется равенство:
i1/0 × i2/1 × i3/2 × i4/3 = i4/0; (11.32)
2) отношение базисного индекса i-го периода к базисному индексу предшествующего (i-1)-го периода дает цепной индекс i-го периода, например, т.е. выполняется равенство:
| i4/0 | = i4/3, (11.33) |
| i3/0 |
Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным индексам и наоборот.
Применение цепного метода исчисления индексов для общих индексов возможно только для агрегатных индексов физического объема с постоянными (фиксированными на уровне одного и того же периода) соизмерителями.
Так, базисный индекс физического объема отчетного периода может быть получен перемножением соответствующих цепных индексов, если соизмеритель принимается на уровне одного и того же периода (формулы 11.23), т.е. выполняется равенство:
Iq,4/0 = Iq,1/0 × Iq,2/1 × Iq,3/2 × Iq,4/3; (11.34)
Два смежных базисных агрегатных индекса физического объема с постоянными соизмерителями Iq,i/0 и Iq,i-1/0 позволяют получить цепной индекс i-го периода Iq,i/і-1 (формулы 11.22), т.е. выполняется равенство:
| Iq,4/0 | = Iq,4/3, (11.35) |
| Iq,3/0 |
Применение цепного метода для агрегатных индексов физического объема оказалось возможным благодаря использованию в качестве соизмерителей фиксированных (соизмеримых, сопоставимых) цен.
Агрегатные индексы качественных показателей всегда является индексами с переменными весами, т.к. количество продукции каждый раз принимается на уровне отчетного периода. Поэтому цепной метод расчета индексов не применим к агрегатным индексам качественных показателей.
Индексы средних величин
При изучении процессов, происходящих в народном хозяйстве, вместе с абсолютными величинами широко используются и средние величины. При оценке динамики экономических явлений средний уровень рассчитывается, как правило, для качественных признаков и определяется он как средняя арифметическая взвешенная по формуле 4.22.
На среднюю величину влияют, с одной стороны, значения признака, которые усредняют, с другой, – частоты вариант. Поэтому при анализе изменения средних величин качественных показателей важно определить, в какой мере оно обусловлено изменением собственно индексируемой величины, а в какой – структурными сдвигами в распределении единиц совокупности.
Структурные сдвиги в экономике – важнейший фактор развития производительных сил общества. Так, например, средняя выработка на одного работающего в какой-либо отрасли промышленности может расти не только благодаря тому, что этот показатель соответственно изменился на отдельных предприятиях, а и потому, что в общей совокупности предприятий этой отрасли увеличился удельный вес предприятий с более высоким уровнем производительности труда на одного работающего. Такие структурные сдвиги влияют на динамику явления, более того, они довольно часто приводят к так называемым «статистическим парадоксам», когда изменение средних величин выходит далеко за пределы изменения исследуемых индивидуальных значений показателей.
Для характеристики изменения средних величин рассчитывают индексы переменного состава, постоянного (фиксированного) состава, структурных сдвигов, формирующих систему взаимосвязанных индексов, представленную формулой, например, для цен:
Ip = Ip × Id, (11.36)
где Ip – индекс цен переменного состава;
Ip – индекс цен постоянного состава;
Id – индекс структурных сдвигов.
Индекс переменного состава характеризует динамику средних величин качественных показателей и отражает как изменение индексируемой величины, так и изменение структуры изучаемого явления. Переменные веса в сравниваемых между собой средних уровнях и обусловили название этого индекса. В общем виде индексом переменного состава качественного признака, в частности, цен, является соотношение его средних уровней.
Механизм расчета индекса переменного состава на примере расчета индекса цен переменного состава, представлен формулой:
| Ip= | p1 | = | Σp1q1 | ÷ | Σp0q0 | . (11.37) |
| p0 | Σq1 | Σq0 |
Индекс переменного состава раскладывается на два субиндекса: индекс постоянного состава и индекс структурных сдвигов (формула 11.36).
Индекс постоянного состава характеризует изменение качественного показателя, которое изучается в условиях неизменной структуры исследуемой совокупности. Этот индекс приводит к уже знакомой агрегатной форме индекса, поэтому его называют индексом постоянного состава.
Механизм расчета индекса постоянного состава на примере расчета индекса цен постоянного состава, представлен формулой:
| Ip= | Σp1q1 | ÷ | Σp0q1 | = | Σp1q1 | . (11.38) |
| Σq1 | Σq1 | Σp0q1 |
Индекс структурных сдвигов характеризует динамику средних значений индексируемого признака, обусловленную влиянием сдвигов в структуре весов индивидуальных значений усредняемого признака единиц совокупности.
Этот индекс не имеет самостоятельного значения, а выступает фактором изменения качественных признаков при изучении влияния сдвигов в структуре весов на изменение индексируемых величин.
Механизм расчета индекса структурных сдвигов на примере расчета индекса структурных сдвигов в продажах товаров по соответствующим ценам, представлен формулой:
| Id= | Σp0q1 | ÷ | Σp0q0 | . (11.39) |
| Σq1 | Σq0 |
Для расчета выше рассмотренных индексов применяется и другая форма записи, которая более четко выделяет факторы, влияющие на изменение среднего показателя, и является достаточно компактной, например:
– индекс цен переменного состава рассчитывается по формуле:
| Ip= | Σp1d1 | . (11.40) |
| Σp0d0 |
где d – доля продукции в натуральном выражении, реализованной по соответствующим ценам, в общем физическом объеме продаж (по формуле 4.11: d = q / Σq);
– индекс цен постоянного состава рассчитывается по формуле:
| Ip= | Σp1d1 | . (11.41) |
| Σp0d1 |
– индекс структурных сдвигов рассчитывается по формуле:
| Id= | Σp0d1 | . (11.42) |
| Σp0d0 |
Абсолютное изменение средней величины с учетом изменения факторов – самого усредняемого признака и структуры, на примере средних цен рассчитывается по формуле:
Δp = Δp(p) + Δp(d), (11.43)
Δp(p) – абсолютный прирост средних цен, обусловленный динамикой цен на проданные товары, рассчитываемый по формулам:
| Δp(p) = | Σp1q1 | - | Σp0q1 | . (11.44) |
| Σq1 | Σq1 |
или
Δp(p) = Σp1d1 - Σp0d1; (11.45)
Δp(d) – абсолютный прирост средних цен, обусловленный изменением структуры физического объема продаж, рассчитываемый по формулам:
| Δp(d) = | Σp0q1 | - | Σp0q0 | . (11.46) |
| Σq1 | Σq0 |
или
Δp(d) = Σp0d1 - Σp0d0. (11.47)
Значение абсолютного прироста средних цен, полученное по формуле 11.43 равняется абсолютному приросту средних цен рассчитанному по формуле:
| Δp = p1 - p0 = | Σp1q1 | - | Σp0q0 | . (11.48) |
| Σq1 | Σq0 |
Пример расчета индексов переменного состава, постоянного состава и структурных сдвигов, а также абсолютного прироста значений средней величины качественного признака, в том числе за счет изменения соответствующих факторов
По данным таблицы 11.6 необходимо проанализировать динамику средней себестоимости изготовления продукции А по трем предприятиям отрасли во втором квартале 2018 г. по сравнению с первым кварталом 2018 г. и охарактеризовать относительное и абсолютное влияние на среднюю отраслевую себестоимость выпуска продукции А как изменения индивидуальных значений себестоимости производства продукции А на рассматриваемых предприятиях, так и изменения структуры выпуска продукции А по трем предприятиям отрасли в рассматриваемом периоде.
Таблица 11.6
| Предприятия | Себестоимость единицы продукции, руб. | Количество изготовленной продукции, тыс. шт. | ||
|---|---|---|---|---|
| І квартал | ІІ квартал | І квартал | ІІ квартал | |
| № 1 | 70,0 | 68,0 | 80 | 120 |
| № 2 | 80,0 | 76,0 | 80 | 120 |
| № 3 | 100,0 | 96,0 | 40 | 160 |
| Всего | х | х | 200 | 400 |
Решение
Для расчета показателей динамики средней себестоимости продукции в формулах 11.21-11.32, заменим букву «p» на букву «z».
Для характеристики динамики средней себестоимости изготовления единицы продукции А и влияния на нее соответствующих факторов рассчитаем индексы переменного, постоянного состава и индексы структурных сдвигов. Для чего в таблице 11.7 приведем результаты расчетов вспомогательных дополнительных показателей, отражающих общие затраты на производство продукции А.
Таблица 11.7
| Предприятия | Себестоимость единицы продукции, руб. | Количество изготовленной продукции, тыс. шт. | Сумма затрат на производство продукции, тыс. руб. | ||||
|---|---|---|---|---|---|---|---|
| І квартал | ІІ квартал | І квартал | ІІ квартал | І квартал | ІІ квартал | условная | |
| z0 | z1 | q0 | q1 | z0q0 | z1q1 | z0q1 | |
| № 1 | 70,0 | 68,0 | 80 | 120 | 5600 | 8160 | 8400 |
| № 2 | 80,0 | 76,0 | 80 | 120 | 6400 | 9120 | 9600 |
| № 3 | 100,0 | 96,0 | 40 | 160 | 4000 | 15360 | 16000 |
| Всего | х | х | 200 | 400 | 16000 | 32640 | 34000 |
Индекс себестоимости переменного состава, рассчитанный по уточненной формуле 11.21, равен: 102,0%.
Значение индекса себестоимости переменного состава свидетельствует о том, что средняя себестоимость продукции А во втором квартале 2018 г. (z1 = 81,6 руб.) по сравнению со средней ее себестоимостью в первом квартале (z0 = 80,0 руб.) по трем предприятиям увеличилась на 2,0 % (102,0 – 100).
Полученный результат должен вызывать удивление, так как на каждом предприятии наблюдалось снижение себестоимости продукции А во втором квартале по сравнению с первым, о чем свидетельствуют значения индивидуальных индексов себестоимости, рассчитанные по уточненной формуле 11.1 для каждого предприятия: для первого предприятия iz1 = 0,97 или 97%; для второго – 0,95 или 95%; для третьего – 0,96 или 96%, т.е. на каждом предприятии наблюдалось снижении себестоимости изготовления продукции А во втором квартале по сравнению с первым, соответственно, на 3%, 5% и 4%.
О снижении себестоимости изготовления продукции А в исследуемом периоде на каждом из рассматриваемых предприятий свидетельствует и расчет индекса себестоимости постоянного состава, проведенный по уточненной формуле 11.22 и данным таблицы 11.7: Iz = 0,96 или 96%. Полученное значение индекса себестоимости постоянного состава не вышло за границы изменения индивидуальных индексов себестоимости и означает то, что при условии постоянной структуры производства продукции А в рассматриваемых кварталах, соответствующей структуре ее производства во втором квартале, себестоимость продукции А во втором квартале по сравнению с первым кварталом в среднем уменьшилась на 4,0%.
Рост средней себестоимости производства продукции А по трем предприятиям объясняется поквартальным изменением удельного веса продукции предприятий в общем выпуске этого изделия (см. табл. 11.8). Во втором квартале 2018 г. доля двух первых предприятий в выпуске продукции А, себестоимость производства на которых ниже, чем на третьем предприятии, уменьшилась, а удельный вес продукции третьего предприятия с более высокой себестоимостью увеличился.
Так, если в базисном периоде (І квартале) на первых двух предприятиях суммарный удельный вес менее затратной продукции составлял 80% (40 + 40) в общем объеме продукции А, то в отчетном периоде (ІІ квартале) он уменьшился до 60% (30 + 30), тогда как доля третьего предприятия увеличилась от 20% до 40%.
Таблица 11.8
| Предприятия | Себестоимость единицы продукции А, руб. | Количество изготовленной продукции А, тыс. шт. | Удельный вес предприятий в производстве продукта А, % | |||
|---|---|---|---|---|---|---|
| І квартал | ІІ квартал | І квартал | ІІ квартал | І квартал | ІІ квартал | |
| z0 | z1 | q0 | q1 | d0 | d1 | |
| № 1 | 70,0 | 68,0 | 80 | 120 | 40 | 30 |
| № 2 | 80,0 | 76,0 | 80 | 120 | 40 | 30 |
| №3 | 100,0 | 96,0 | 40 | 160 | 20 | 40 |
| Всего | х | х | 200 | 400 | 100 | 100 |
Для количественной оценки влияния фактора изменения структуры выпуска продукции А по предприятиям отрасли рассчитаем индекс структурных сдвигов, характеризующий степень влияния структурных сдвигов на среднюю себестоимость, с помощью уточненной формулы 11.23 на основе данных таблицы 11.7: Id = 1,0625 или 106,25%.
Благодаря увеличению удельного веса продукции третьего предприятия, имеющего более высокий уровень себестоимости, в общем объеме выпуска продукции А, средняя себестоимость увеличилась на 6,25%, что и обусловило общий рост средней себестоимости продукции А на 2,0%.
Рассчитанный индекс отвечает на вопрос: как изменилась бы общая средняя себестоимость продукции А по отрасли при условии изменения только удельного веса предприятий в производстве этой продукции при неизменной себестоимости на каждом предприятии.
Таким образом, в приведенном примере структурные сдвиги можно рассматривать как негативный фактор, поскольку они привели к дополнительным затратам в целом по отрасли.
Итак, рост средней себестоимости продукции А на 2,0% обусловлен ее ростом за счет изменения внутриотраслевой структуры производства на 6,25% при снижении себестоимости производства продукции на каждом предприятии в среднем на 4%.
Рассмотренную закономерность иллюстрирует система взаимосвязанных индексов, представленная с помощью уточненной формулы 11.20: Iz = 1,02.
Расчет индексов себестоимости переменного, постоянного состава и структурных сдвигов с помощью уточненных формул 11.24-11.26 проведем на основе данных таблицы 11.9.
Таблица 11.9
| Предприятия | Себестоимость единицы продукции, руб. | Удельный вес предприятий в производстве продукта А | Произведение себестоимости продукции А на удельный вес, руб. | ||||
|---|---|---|---|---|---|---|---|
| І квартал | ІІ квартал | І квартал | ІІ квартал | І квартал | ІІ квартал | условное | |
| z0 | z1 | d0 | d1 | z0d0 | z1d1 | z0d1 | |
| № 1 | 70,0 | 6,8 | 0,40 | 0,30 | 28,0 | 20,4 | 21,0 |
| № 2 | 80,0 | 7,6 | 0,40 | 0,30 | 32,0 | 22,8 | 24,0 |
| №3 | 100,0 | 9,6 | 0,20 | 0,40 | 20,0 | 38,4 | 40,0 |
| Всего | х | х | 1,00 | 1,00 | 80,0 | 81,6 | 85,0 |
Индекс себестоимости переменного состава, рассчитанный по уточненной формуле 1.24 по данным таблицы 11.9, равен: Iz = 1,020.
Индекс себестоимости постоянного состава, рассчитанный по уточненной формуле 11.25 по данным таблицы 11.9, равен: Iz = 0,960.
Индекс структурных сдвигов, рассчитанный по уточненной формуле 11.26 по данным таблицы 11.9, равен: Id = 1,0625.
Значения индексов себестоимости, рассчитанные по уточненным формулам 11.24-11.26, абсолютно совпадают с индексами себестоимости, исчисленными по уточненным формулам 11.21-11.23, и получены менее трудоемким способом.
Абсолютный прирост средней себестоимости производства продукции А по трем предприятиям во втором квартале 2018 г. по сравнению с первым кварталом, исчисленный по уточненной формуле 11.32, составил:
Δz = z1-z0 = 81,6-80,0 = 1,6 руб.
Рассмотрим абсолютные значения степени влияния отдельных факторов (изменения себестоимости изготовления продукции А на предприятиях и структуры ее производства) на эту величину.
Абсолютный прирост средней себестоимости продукции А во втором квартале 2018 г. по сравнению с первым кварталом, обусловленный изменением себестоимости ее производства на каждом предприятии, исчисленный по уточненным формулам 11.28 или 11.29, составил:
Δz(z) = 81,6 – 85,0 = -3,4 руб., т.е. средняя себестоимость изделия А при условии постоянной структуры ее производства, соответствующей второму кварталу, снизилась на 3,4 руб.
Абсолютный прирост средней себестоимости продукции А во втором квартале 2013 г. по сравнению с первым кварталом, обусловленный изменением структуры ее производства, исчисленный по уточненным формулам 11.30 или 11.31, составил:
Δz(d) = 85,0 – 80,0 = 5,0 руб., т.е. средняя себестоимость продукции А за счет этого фактора выросла на 5,0 руб.
Итак, снижение средней себестоимости продукции А во втором квартале 2018 г. по сравнению с первым кварталом этого же года за счет уменьшения себестоимости ее производства на каждом предприятии на 4,0% , что в абсолютном выражении составило 3,4 руб., при одновременном ее увеличении на 6,25% или 5,0 руб. за счет изменения структуры производства в сторону более затратной продукции предприятия № 3, определило рост средней себестоимости производства продукции А по трем предприятия на 2,0 % или 1,6 руб. В соответствии с равенством, представленным уточненной формулой 11.43 имеем:
Δz = Δz(z) + Δz(d) = - 3,4 - 5,0 = +1,6 руб.
Таким образом, общие затраты трех предприятий на производство продукции А во втором квартале 2018 г. по сравнению с первым кварталом 2018 г. только в результате изменения удельного веса предприятий в производстве должны были увеличиться на 2000 тыс. руб. (5,0 × 400). Однако снижение себестоимости выпуска продукции А на каждом из трех предприятий и в среднем на всех трех предприятиях на 4% обеспечило экономию средств на каждом изделии в размере 3,4 руб. и все затраты на его производство во втором квартале сократились на 1360 тыс. руб. (3,4 × 400). А это значит, что общие затраты на производство 400 тысяч изделий А во втором квартале увеличились с учетом этих двух факторов только на 640 тыс. руб. (1,6 × 400) вместо 2000 тыс. руб.
Территориальные индексы
Рассмотренные выше статистические индексы используются главным образом для изучения развития явлений и процессов во времени, а также для анализа выполнения плановых заданий и норм. Однако индексный метод широко применяется и для территориальных сравнений, для сравнения предпринимательской и других видов деятельности отдельных регионов страны. Огромное значение имеет индексный метод в международной статистике для сопоставления показателей социально-экономического развития отдельных стран.
Территориальные индексы – это разновидность относительных величин сравнения, когда сопоставляются показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам).
Общие принципы построения территориальных индексов в значительной мере идентичны тем, какими руководствуются при моделировании динамических индексов. Вместе с тем в отличие от них при построении территориальных индексов имеет место некоторая специфика при выборе базы сравнения. Например, сравнивая два региона, можно каждый из них принять как в качестве сравниваемого, так и качестве базы сравнения. Кроме того, при определении общих территориальных индексов отдельную проблему составляет выбор весов-соизмерителей.
Механизм построения территориальных индексов рассмотрен на примере индекса товарооборота и его субиндексов.
Территориальный индекс товарооборота (IQ,А/Б) представляет собой отношение суммы выручки от продажи товаров в одном из районов к аналогичному показателю в другом и рассчитывается по формуле:
| IQ,А/Б = | ΣpAqA | . (11.49) |
| ΣpБqБ |
где район А принят в качестве сравниваемого района, а район Б – базы сравнения;
рА и рБ – соответственно цены на определенные товары в районе А и районе Б;
qА и qБ – соответственно физические объемы продаж этих товаров в районе А и районе Б.
Различие объемов товарооборота по районам вызвано различием количества проданных товаров и цен на них.
Территориальный индекс физического объема товарооборота (Iq,А/Б), характеризующий различия в количестве проданных товаров в натуральном выражении в районе А по сравнению с физическим объемом продаж этой же продукции в районе Б, рассчитывается по формуле:
| Iq,А/Б = | ΣqA × p | . (11.50) |
| ΣqБ × p |
где p – средняя межрайонная цена товара каждого вида, рассчитываемая по формуле:
| p = | pA×qA + pБ×qБ | . (11.51) |
| qA + qБ |
Использование в территориальных индексах физического объема средних межрайонных цен товара каждого вида позволяет избежать влияния различий в ценах на товары по районам на соотношение объемов их реализации в натуральном выражении.
Территориальный индекс цен (Iр,А/Б), характеризующий различия в ценах на проданные товары в районе А по сравнению с ценами на аналогичные товары района Б, рассчитывается по формуле:
| Iр,А/Б = | ΣpA × q | . (11.52) |
| ΣpБ × q |
где q – суммарный по двум районам объем продаж каждого вида товара, рассчитанный по формуле:
q = qA + qБ. (11.53)
Использование в территориальном индексе цен в качестве весов-соизмерителей общего физического объема продаж товаров каждого вида позволяет преодолеть влияние изменений в структуре реализованных товаров по районам.
Более сложные, чем ранее, взвешивающие показатели применяются для того, чтобы результаты расчета были обратимыми, т.е. чтобы выполнялись соотношения, представленные формулами:
| Iq,А/Б = | 1 | (11.54). |
| Iq,Б/А |
| Ip,А/Б = | 1 | . (11.55) |
| Ip,Б/А |
Условия индексной модели Iq,А/Б × Iр,А/Б = IQ,А/Б и Iq,Б/А × Iр,Б/А = IQ,Б/А в данном случае могут нарушаться, хотя, как правило, и не очень существенно.
Пример расчета территориальных индексов
Реализация фруктов на двух городских рынках города N в 2018 г. представлена данными таблицы 11.10. Необходимо охарактеризовать соотношения стоимости фруктов, проданных на рынке К по сравнению с рынком Ц, а также уровней цен на фрукты по рынкам и физических объемов их продаж.
Таблица 11.10
| Фрукты | Рынок К | Рынок Ц | ||
|---|---|---|---|---|
| Модальная цена за 1 кг, руб. | Количество проданных фруктов, ц | Модальная цена за 1 кг, руб. | Количество проданных фруктов, ц | |
| Яблоки | 50 | 40 | 40 | 50 |
| Груши | 70 | 70 | 60 | 80 |
| Персики | 120 | 30 | 130 | 20 |
Решение
Для сравнения товарооборота фруктов на рынках города N в качестве базы сравнения примем данные о продажах фруктов на рынке Ц.
Территориальный индекс товарооборота фруктов, рассчитанный по формуле 11.49, равен: IQ,К/Ц = 1,117, т.е. стоимость фруктов, проданных на рынке К, в 1,1 раза или на 11,7 % (1,117 × 100 – 100) больше, чем на рынке Ц.
Различие объемов товарооборота по рынкам вызвано различием количества проданных фруктов и цен на них.
Для оценки влияния различий в количестве проданных фруктов на уровень их товарооборота на рынках города рассчитаем по формуле 11.51 средние цены продаж на рынках города соответственно яблок, груш и персиков:
pяб = 44,4 руб.;
pгр = 64,7 руб.;
pпер = 124,0 руб.
Территориальный индекс физического объема товарооборота фруктов на рынках города, рассчитанный по формуле 11.50, равен: Iq,К/Ц = 1,015 или 101,5 %.
Полученное значение индекса показывает, что количество фруктов, проданных на рынке К на 1,5 % больше общего количества фруктов, реализованных на рынке Ц. При этом индивидуальные территориальные индексы физического объема продаж, соответственно, яблок, груш и персиков составили: iq,яб,К/Ц = 0,8 или 80,0%; iq,гр,К/Ц = 0,875 или 87,5%; iq,пер,К/Ц = 1,5 или 150,0%. Таким образом, рост физического объема продаж персиков на 50,0% на рынке К по сравнению с физическим объемом их продаж на рынке Ц, при одновременном уменьшении количества проданных яблок и груш, соответственно, на 20,0% и 12,5%, обусловил общее увеличение количества проданных фруктов на рынке К по сравнению с их реализацией в натуральном выражении на рынке Ц на 1,5 %.
Для характеристики влияния на количественную разницу товарооборота фруктов на рынке К по сравнению с рынком Ц различий в ценах их продаж рассчитаем по формуле 10.53 суммарный по двум рынкам объем продаж в натуральном выражении, соответственно, яблок, груш и персиков: qяб = 90 ц; qгр = 150 ц; qпер = 50 ц.
Территориальный индекс цен на фрукты на рынках города, рассчитанный по формуле 11.52, равен: Ip,К/Ц = 1,099 или 109,9%, т.е. цены на рынке К выше, чем на рынке Ц в среднем на 9,9 %. При этом индивидуальные территориальные индексы цен, соответственно, яблок, груш и персиков составили: ip,яб,К/Ц = 1,25 или 125,0%; ip,гр,К/Ц = = 1,167 или 116,7%; ip,пер,К/Ц = 0,923 или 92,3%. Таким образом, рост цен на яблоки и груши, соответственно, на 25,0% и 16,7% на рынке К по сравнению с рынком Ц, при одновременном снижении цен на персики на 7,7%, обусловил средний рост цен на фрукты на рынке К по сравнению с рынком Ц на 9,9%.
