Экономическая оценка эффективности инвестиций
Основные положения по оценке эффективности инвестиций
Основные подходы и порядок проведения расчетов эффективности капитальных вложений по всему инвестиционному циклу проводились в нашей стране по соответствующим методикам, разработанным коллективами ученых и принятыми органами управления экономикой.
При рассмотрении эволюции (генезиса) методов определения экономической эффективности инвестиций авторами предлагается остановиться на сущности экономической эффективности капитальных вложений.
Сущность экономической эффективности инвестиций заключается в повышении производительности труда, т. е. в снижении стоимости продукции. Эффективность капитальных вложений имеет два аспекта: экономический и социальный. При определении экономического аспекта эффективности капитальных вложений достигается наиболее полный учет затрат в основные и смежные производства, выявляется общая сумма эффекта от этих затрат как у производителя, так и у потребителя.
Общая экономическая эффективность определяется как отношение эффекта к капитальным вложениям, вызвавшим этот эффект. В качестве обобщающих показателей принимают: показатель окупаемости капитальных вложений, характеризующий сроки возвратности вкладываемых средств, и показатель удельных капитальных вложений, позволяющий оценить меру ресурсосбережения (капиталоемкости) при обеспечении заданного объема прироста продукции, работ, услуг.
К оценочным показателям относятся:
- производительность труда;
- фондоотдача;
- себестоимость продукции;
- продолжительность строительства, освоение проектных мощностей;
- показатели, характеризующие социальный эффект, в сравнении с социальными нормами;
- качество и технический уровень продукции.
Оценка социальных результатов инвестиций предполагает, что проект соответствует социальным нормам, стандартам и условиям соблюдения прав человека. К основным видам социальных результатов инвестиций относятся:
- изменение количества рабочих мест в регионе;
- улучшение жилищных и культурно-бытовых условий работников;
- изменение условий труда работников;
- изменение уровня здоровья работников и населения;
- экономия свободного времени населения.
В стоимостной оценке социальных результатов учитывается только их самостоятельная значимость. Затраты, необходимые для достижения социальных результатов проекта или обусловленные социальными условиями реализации проекта, учитываются в расчетах эффективности в общем порядке, и в стоимостной оценке социальных результатов не отражается.
В развитии теории и практики оценки определения экономической эффективности инвестиций можно условно выделить три периода.
Первый период (до 1917 г.). В трудах А. Л. Васютинского и В. А. Яцыны, изданных в 1905–1908 гг., в качестве показателя для выбора наилучшего (выгодного) варианта инвестиционного проекта предполагалось использовать одну из форм показателя сравнительной экономической эффективности капитальных вложений, представляющего собой сумму эксплуатационных расходов и части единовременных затрат, соответствующий процент на строительный капитал. В этом случае процент на строительный капитал выступал как норма дохода на вкладываемый капитал. В работах В. А. Сокольского, опубликованных в 1910–1912 гг., обращалось внимание на то, что целесообразно при оценке инвестиционных решений соизмерять капитальные вложения с последующими эксплуатационными расходами, рассчитывать срок окупаемости увеличения затрат на строительство за счет снижения расходов на эксплуатацию объектов. В. А. Сокольский доказал на многочисленных практических примерах, что нельзя игнорировать при выборе тех или иных конструкций и содержаний основного положения экономичности: «Не все то дешево потом, за что заплачено сейчас дешевле». Необходимо тщательное обоснование выгодности первоначального капитала, которое перекрывается избытком постоянных затрат, необходимых для эксплуатации сооружений. В книге Ю. В. Ломоносова «Научные проблемы эксплуатации железных дорог», вышедшей в 1912 г., указывается на целесообразность оценки сроков погашения стоимости строительства экономией годовых издержек при эксплуатации железных дорог.
Второй период (1917–1990 гг.) – это период централизованной плановой экономики. После 1917 г. важным этапом формирования методологии оценки экономической эффективности инвестиций в условиях социализма с учетом интересов всего народного хозяйства явилась разработка плана ГОЭЛРО. При формировании этого плана для обоснования экономической эффективности варианта развития были выполнены расчеты по приведенным затратам с добавлением к текущим издержкам капитальных вложений (в процентах).
Стройки-гиганты в годы первых пятилеток требовали совершенствования экономических обоснований инвестиционных проектов и планов. Обоснование строительства таких строек, как Магнитогорский и Кузнецкий металлургические комбинаты, Днепрогэс, Турксиб, железнодорожная магистраль Москва – Донбасс и другие нуждались в более глубоком анализе инвестиционных вложений и текущих издержек производства, методах расчета стоимости строительства и расходов на эксплуатацию объектов. В этот период были опубликованы труды по технико-экономическому анализу строительства объектов энергетики, транспорта, тяжелой промышленности. В 1934 г. Л. П. Юшков в своей книге «Проектирование крупных предприятий тяжелой промышленности (на примере металлургического предприятия)» указал на необходимость применения комплексного подхода при проектировании крупных промышленных проектов, при котором должны быть взаимосвязаны все части проекта (экономические, технологические, организационные). Этот комплексный подход направлен как на расширение выпуска продукции и обеспечение благоприятных условий труда, техники безопасности, так и на экономию общественно необходимых издержек.
Далее научное развитие показателей оценки экономической эффективности инвестиций носило коллективный характер. В 1949–1954 гг. экономисты проводили дискуссии по экономическим проблемам социализма, в которых обсуждался вопрос об определении эффективности капитальных вложений, но положительных научно обоснованных решений принято не было.
Большим шагом вперед явилось издание в 1956 г. Государственным комитетом Совета министров СССР по новой технике и другими центральными органами «Временной типовой методики определения эффективности внедрения новой техники». В этом документе был одобрен метод окупаемости капитальных вложений с использованием ряда технико-экономических показателей эффективности. Однако в методике не были отражены важные методологические вопросы, возникавшие в то время при определении экономической эффективности, поэтому методика не внесла кардинальных изменений в практику экономических расчетов в инвестиционных проектах.
Для выработки новой методики необходимо было прежде всего обобщить накопленный опыт и решить, наконец, целый ряд важнейших теоретических и методологических вопросов проблемы определения эффективности инвестиций. К их числу относятся:
- сущность экономической эффективности капитальных вложений и новой техники в условиях социалистического производства и связь этой проблемы с производительностью труда, действием закона стоимости и стоимостными категориями;
- методы соизмерения дополнительных капитальных вложений и экономии текущих затрат, обеспечивающие правильное определение эффективности проектных решений;
- методы определения нормативных сроков окупаемости или коэффициентов эффективности;
- роль фактора времени при выборе направлений капитальных вложений;
- методы определения влияния на эффективность разновременности капитальных вложений и другие вопросы.
В 1958 г. состоялась Всесоюзная научно-техническая конференция по проблемам определения экономической эффективности капитальных вложений и новой техники в народном хозяйстве СССР.
Конференция отметила, что сущность экономической эффективности капитальных вложений и новой техники заключается в повышении производительности общественного труда, т. е. снижении стоимости продукции. Этим была признана необходимость учета действия закона стоимости при определении эффективности капитальных вложений.
Результатом данной конференции были рекомендации, обсуждающейся проблемы, которые в дальнейшем легли в основу Типовой методики определения экономической эффективности капитальных вложений и новой техники. Методика использовалась для разработки и последовательной корректировки инструкций по определению экономической эффективности капитальных вложений и новой техники в основных отраслях народного хозяйства.
В условиях протекания стабильного и контролируемого государством процесса накопления в СССР для обоснования выбора того или иного инвестиционного проекта была разработана и широко использовалась система показателей сравнительной экономической эффективности капитальных вложений. Как известно в нее входили следующие основные показатели:
1. Срок окупаемости (S) – это прямой показатель экономической эффективности капитальных вложений. Данный показатель определяется в годах и рассчитывается по следующей формуле:
| S = | K2 - K1 | (3) |
| Z1 - Z2 |
где K1, K2 – капитальные вложения в рублях по вариантам (K2 > K1);
Z1, Z2 – себестоимость годового объема продукции (работ, услуг) в рублях по соответствующим вариантам (Z1 > Z2).
Таким образом, очевиден тот факт, что этот показатель рассчитывался для сравнения двух предлагаемых вариантов осуществления капитальных вложений, один из которых считается выгодным на объеме капиталовложений (K1 < K2), а другой – на издержках производства, реализации (Z2 > Z1). Выбор конкретного варианта производился в зависимости от результата сравнения полученного фактического срока окупаемости с нормативным значением этого показателя. Если S < Sn, то более выгодным признается второй вариант, требующий больших вложений (K2), и наоборот.
Экономический смысл показателя «срок окупаемости» (S) состоит в том, что он отражает период, во время которого затраты на дополнительные капитальные вложения окупаются за счет снижения себестоимости продукции (работ, услуг), вызванного этими капиталовложениями. Чем меньше срок окупаемости, тем эффективнее вариант инвестирования.
2. Коэффициент сравнительной эффективности (Э) является обратным показателем эффективности капитальных вложений, определяется в коп/руб. по следующей формуле:
| Э = | Z1 - Z2 | (4) |
| K2 - K1 |
Отсюда следует, что показатель сравнительной эффективности отражает величину экономии от снижения себестоимости выпускаемой продукции, приходящейся на 1 руб. дополнительных капиталовложений. Именно этот показатель подлежит нормированию со стороны государства и является, таким образом, средством регулирования меры экономической эффективности капитальных затрат по народному хозяйству. При этом нормативный коэффициент сравнительной эффективности капитальных вложений (Эн) выступает, с одной стороны, самостоятельным экономическим показателем, а с другой стороны – базовой величиной для исчисления показателей эффективности капитальных вложений в ходе многовариантного инвестиционного анализа. Впервые значение коэффициента сравнительной эффективности инвестиций (Эн) было установлено для 11-й пятилетки.
3. Затраты (З). При помощи этого показателя удобно проводить сравнительный анализ экономической эффективности капитальных вложений при большом числе вариантов их осуществления. Затраты исчисляются по формуле (за один год осуществления вариантов вложений):
З = KiЭн + Zi, (5)
где Эн – нормативный коэффициент сравнительной эффективности капитальных вложений;
Ki, Zi – капитальные вложения и издержки производства, приходящиеся на единицу продукции по сравниваемым вариантам.
Затраты, рассчитанные за весь срок окупаемости проектов, определяются следующим образом:
З1 = ZSн + K, (6)
где Sн – нормативный срок окупаемости (1/Эн);
K, Z – капитальные вложения и издержки производства на общий объем продукции по сравниваемым вариантам. Лучшим вариантом является тот, по которому величина затрат наименьшая.
4. Годовой экономический эффект (Эг) – это обобщающий показатель экономической эффективности организационно-технических мероприятий, который определяется по формуле
Эг = (З1 – З2) × V, (7)
где V – объем годового выпуска продукции, соответствующей выбранному оптимальному варианту;
З1, З2 – затраты по вариантам капитальных вложений.
Чем выше абсолютное значение показателя Эг, тем более обоснованным считается выбор оптимального варианта из имеющихся в распоряжении инвестора вариантов.
5. Коэффициент приведения (Кп) использовали, когда финансирование того или иного варианта капитальных вложений предусматривало не единовременные вложения, а распределение их по годам, т. е. для корректировки стоимости настоящих инвестиционных расходов к определенному моменту времени в будущем (как правило, по окончании срока осуществления инвестиционных расходов).
Этот показатель рассчитывается следующим образом:
Кп = (1 + Эн)nT-n (8)
При необходимости пересчета абсолютного значения планируемых в будущем показателей к настоящей оценке рассчитывали коэффициент дисконтирования:
| Д = | 1 | (9) |
| (1 + Эн)n |
где nT– расчетный год; п – год, затраты и результаты которого приводятся к расчетному году;
Таким образом, разность (nT – n) показывает, на сколько лет капитальные вложения замораживаются, т. е. не дают отдачи в виде доходов от реализации выпускаемой продукции (работ, услуг).
В случае распределения необходимых капитальных вложений по разным периодам времени обобщающим показателем сравнения вариантов их осуществления выступает суммарный чистый доход от проекта (dсум).
Он рассчитывается по следующей формуле:
dсум = ΣКn×dn (10)
где Кn – коэффициент приведения (дисконтирования);
dn – сумма чистого дохода по годам реализации проекта.
Такова система показателей экономической оценки вариантов осуществления капитальных вложений, используемая длительное время в ходе инвестиционного анализа в СССР.
Третий период (с 1990 г. по настоящее время). Вышеизложенная система показателей экономической эффективности капиталовложений перестала удовлетворять требованиям современных экономистов, аналитиков в инвестиционной сфере.
Главная причина этого явления заключается в том, что принципиальные черты «советской» системы показателей эффективности инвестиций не находят приложения в новой экономической системе России, т. е. в условиях транзитивной экономики.
Во-первых, все показатели, применявшиеся в отечественной методике, ориентированы на снижение издержек производства продукции (работ, услуг) и характеризуют явление экономики на затратах вследствие произведенных капитальных вложений.
Действительно, когда инвестиционная политика и весь экономический механизм находились под полным контролем со стороны государства, когда полностью отсутствовал такой инструмент экономического регулирования, как налоговая система, жесткого нормативного распределения доходов и расходов предприятий, отсутствия рынков кредитов и ценных бумаг, задание целевой функции инвестиционных затрат в виде минимизации издержек производства было вполне оправданным.
В современных условиях развития экономики, напротив, этот методологический подход не вписывается в настоящую систему экономических оценок.
В рыночной экономике явление «снижение себестоимости продукции (работ, услуг)» неравнозначно явлению «увеличение прибыли в распоряжении предприятия», а в условиях становления конкурентной экономики именно максимизация прибыли выступает главным мотивом деятельности предпринимателей. Неравнозначность явлений снижения себестоимости и увеличения прибыли обусловливается, с одной стороны, существованием сложной налоговой системы, с другой стороны, негарантированностью реализации продукции и, соответственно, возмещения издержек и получения определенных доходов. Прежняя отечественная методика строит свои аналитические показатели, опираясь лишь на удельные издержки и планируемый объем производства, при этом совершенно не принимая во внимание планируемые доходы и прибыль от реализации продукции, в чем и состоит, собственно, весь инвестиционный анализ в рыночной экономике.
Кроме того, как уже отмечалось выше, базой исчисления основных показателей экономической эффективности капитальных вложений являлось нормативное значение коэффициента сравнительной эффективности Эн. Сегодня в связи с изменением мотивации осуществления предпринимательской деятельности, в силу своего экономического содержания показатель Эн утрачивает роль основы для расчета показателей, характеризующих эффективность инвестиционных проектов. Совершенно закономерно в этой связи то, что сравнительные расчеты, включающие показатели, исчисленные как на базе критерия минимума затрат (прежняя методика), так и на базе критерия максимума дохода (прибыли) по зарубежной методике, одновременно сделанные на основе анализа одного инвестиционного проекта, как правило, дают прямо противоположные рекомендации по принятию окончательного решения.
Как уже отмечалось, оценка эффективности инвестиций имеет огромный научный и практический интерес, поскольку от того, насколько объективно и всесторонне осуществлена эта оценка, зависят сроки окупаемости вложенного капитала, темпы развития фирмы, а также решение многих проблем социально-экономического развития страны. А объективность и всесторонность оценки эффективности инвестиционных проектов, в свою очередь, в значительной мере определяются использованием современных методов проведения такой оценки.
Рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования, утвержденные совместным постановлением Госстроя России, Минэкономики РФ, Минфина РФ и Госкомпромом России от 31 марта 1994 г. № 7-12/47, содержат следующие принципы, используемые в зарубежной практике некоторых стран.
1. Принцип оценки возврата инвестируемого капитала на основе показателя денежного потока (cash flow), который формируется за счет чистой прибыли и амортизационных отчислений в процессе реализации инвестиционного проекта.
2. Принцип обязательного приведения к настоящей стоимости будущих поступлений, т. е. денежного потока. Действительно, инвестиционный процесс длится порой не один год. В течение времени реализации проекта увеличивается стоимость вложенных денег сегодня. Поэтому за исключением денег, вложенных сегодня, все последующие инвестируемые суммы должны быть приведены к настоящей стоимости.
3. Принцип выбора дифференцированной ставки процента (дисконтной) в процессе дисконтирования потока для различных инвестиционных проектов. При этом размер предлагаемого дохода формируется с учетом следующих факторов:
- средней реальной депозитной ставки;
- темпа инфляции (или премии за инфляцию);
- премии за риск;
- премии за низкую ликвидность.
Соблюдение этого принципа весьма важно при сравнении двух и более инвестиционных проектов, различающихся разными уровнями риска или продолжительностью осуществления.
4. Принцип гибкой системы использования ставки процента для дисконтирования денежных потоков в зависимости от целей оценки инвестиционного проекта. Так, при расчете различных показателей эффективности инвестиций в качестве ставки процента, выбираемой для дисконтирования, могут быть использованы:
- средняя депозитная и кредитная ставка;
- индивидуальная норма доходности инвестиции с учетом уровня инфляции, риска и ликвидности инвестиций;
- альтернативная норма доходности по другим возможным видам инвестиций;
- норма доходности по текущей хозяйственной деятельности.
Наряду с вышеперечисленными принципами в указанных Рекомендациях по оценке эффективности инвестиционных проектов предлагается деление показателей эффективности инвестиционных проектов на следующие виды:
1) показатели бюджетной эффективности, отражающие финансовые последствия осуществления проекта для федерального, регионального или местного бюджетов;
2) показатели народнохозяйственной эффективности, отражающие эффективность проекта с точки зрения интересов всего народного хозяйства в целом, а также участвующих в осуществлении проекта регионов (субъектов федерации), отраслей, организаций, предприятий;
3) показатели коммерческой эффективности (финансовое обоснование) проекта, учитывающие финансовые последствия реализации проекта для его непосредственных участников. По сути, расчету эффективности должны предшествовать маркетинговые исследования и все необходимые согласования с местными органами самоуправления о дополнительном осуществлении проекта.
Все методы расчета эффективности инвестиционных проектов, за редким исключением, осуществляются с помощью постоянно обновляемого программного обеспечения, т. е. с использованием компьютерных технологий, адаптированных к условиям российской практики,
В настоящее время оценка эффективности инвестиций проводится на основе «Методических рекомендаций по оценке эффективности инвестиционных проектов (вторая редакция), утвержденных Министерством экономики РФ, Министерством финансов РФ, Государственным комитетом по строительству, архитектурной и жилищной политике. Данные рекомендации содержат описание корректных методов расчета эффективности инвестиционных проектов. В этих целях рекомендации предусматривают:
- унификацию терминологии и перечня показателей эффективности инвестиционных проектов, разрабатываемых различными проектными организациями, а также подходов к их определению;
- систематизацию требований, предъявляемых к предпроектным и проектным материалам при рассмотрении расчетов эффективности инвестиционных проектов, а также к составу, содержанию и полноте исходных данных для проведения расчетов;
- учет особенностей реализации отдельных видов инвестиционного проекта, обусловливающих использование нестандартных методов оценки эффективности;
- установление требований к экономическому сопоставлению вариантов технических, организационных и финансовых решений, разрабатываемых в составе отдельного инвестиционного проекта.
Методические рекомендации предназначены для предприятий и организаций всех форм собственности, участвующих в разработке, экспертизе и реализации инвестиционных проектов.
Рекомендации могут быть приняты в качестве основы для создания нормативно-методических документов по разработке и оценке эффективности отдельных видов инвестиционных проектов, учитывающих их специфику. Они используются:
- для оценки эффективности и финансовой реализуемости инвестиционных проектов;
- для оценки эффективности участия в инвестиционном проекте хозяйствующих субъектов;
- для принятия решений о государственной поддержке инвестиционных проектов;
- для сравнения альтернативных инвестиционных проектов, вариантов инвестиционных проектов и оценки экономических последствий выбора одного их них;
- для оценки экономических последствий отбора для реализации группы инвестиционных проектов из некоторой их совокупности при наличии фиксированных финансовых и других ограничений;
- для принятия экономически обоснованных решений об изменении в ходе реализации инвестиционных проектов в зависимости от вновь выявляющихся обстоятельств (экономический мониторинг).
Финансово-экономическая оценка инвестиционных проектов занимает важное место в процессе обоснования и выбора возможных вариантов вложения денежных средств в реальный сектор экономики. При всех прочих благоприятных характеристиках проекта он не будет принят к реализации, если не обеспечит:
- возмещения вложенных денежных средств за счет доходов от реализации товаров и услуг;
- получения прибыли, обеспечивающей рентабельность инвестиций не ниже желательного для фирмы уровня;
- окупаемости инвестиций в пределах срока, приемлемого для фирмы.
Определение реальности достижения именно таких результатов инвестиционных операций и является ключевой задачей оценки финансово-экономических параметров любого проекта вложения средств в реальные активы.
Проведение такой оценки всегда является достаточно сложной задачей, что порождается рядом факторов:
- во-первых, инвестиционные расходы могут осуществляться либо разово, либо неоднократно на протяжении достаточно длительного периода времени;
- во-вторых, длителен и процесс получения результатов от реализации инвестиционных проектов (т. е. более одного года);
- в-третьих, осуществление длительных операций приводит к росту неопределенности при оценке всех аспектов инвестиций.
Именно наличие этих факторов породило необходимость в создании современных методов оценки инвестиционных проектов, позволяющих принимать достаточно обоснованные решения с минимально возможным уровнем погрешности (ошибок).
В условиях развивающейся экономики были разработаны методические рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования. Эти рекомендации основываются на методологии, применяемой в современной международной практике. Используются также подходы, выработанные при создании отечественных методик.
Объективность оценки эффективности инвестиций определяется использованием современных методов проведения оценки. Коммерческая состоятельность – это заключительное звено проведения прединвестиционных исследований, она должна базироваться на информации, полученной и проанализированной на всех предшествующих этапах работы. Коммерческая оценка представляет собой интегральный подход к анализу инвестиционных вложений.
Каковы же общие критерии коммерческой привлекательности инвестиций?
Кратко их можно обозначить как финансовая состоятельность вложений (финансовая оценка) и эффективность инвестиций (экономическая оценка). По этим критериям проводят соответственно финансовую и экономическую оценки инвестиционных проектов.
Оба подхода, или метода, взаимно дополняют друг друга. Первый используется для анализа ликвидности (платежеспособности) инвестиций в ходе его реализации. Во втором заключается потенциальная способность инвестиций сохранить покупательную ценность вложенных средств и обеспечить достаточный темп их прироста.
Рассмотрим коммерческую оценку инвестиционных проектов (рис. 19).
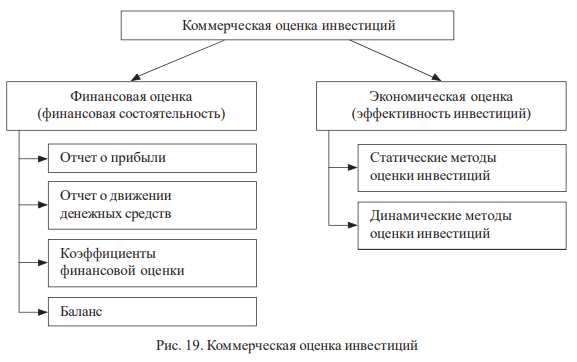
Финансовая оценка инвестиций должна обеспечить достижение двух главных целей:
- получение приемлемой прибыли на вложенный капитал;
- поддержание устойчивого финансового состояния предприятия.
Анализ того, насколько успешно будут решаться эти задачи, а также сопоставление между собой различных инвестиционных проектов и вариантов расчетов с различными наборами исходных данных могут быть выполнены с помощью коэффициентов финансовой оценки.
Для решения вышеуказанных задач используются следующие группы коэффициентов финансовой оценки проекта:
- рентабельности;
- оборачиваемости (деловой активности);
- ликвидности (финансовой устойчивости).
В прил. 8 представлены наиболее часто используемые коэффициенты финансовой оценки инвестиций. Все показатели оборачиваемости используются для определения скорости движения денежных средств по различным текущим счетам предприятия. В силу известной специфики подготовки исходных данных для оценки инвестиций подобная информация не будет иметь какой-либо особой ценности. Определенный интерес вызывает только коэффициент оборачиваемости оборотного капитала (Оок). Показатели, входящие в только что рассмотренные категории, отражают успешность предполагаемой к осуществлению производственной и маркетинговой политики.
Для России рекомендуется использовать следующие значения коэффициентов ликвидности: Лобщ = 1,5 – 2,0; Лсроч = 0,5 – 1,2; Лабс = 0,2 – 0,25.
Приведенные коэффициенты финансовой оценки проекта позволяют рассматривать его с различных позиций и тем самым анализировать устойчивость финансового состояния на каждом шаге расчета.
Другим, не менее важным направлением использования коэффициентов является выбор таких источников финансирования, которые обеспечивают превышение рентабельности акционерного капитала над рентабельностью всех активов.
В этом случае следует пользоваться формами бухгалтерской отчетности предприятия, а состав коэффициентов и расчетные формулы могут несколько отличаться, что объясняется меньшим уровнем детализации исходных данных при планировании инвестиционного проекта в связи с их прогнозным характером.
Теория инвестиционного анализа предусматривает использование определенной системы аналитических методов и показателей. Для оценки экономической эффективности проектов наиболее часто применяются динамические методы оценки эффективности инвестиций (рис. 20).
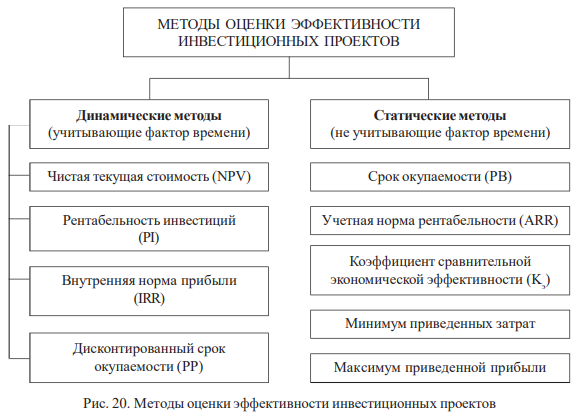
Несмотря на существенные различия между видами инвестиций и многообразием условий их реализации, оценка эффективности инвестиций и их экспертиза должны производиться в определенном смысле единообразно, на основе единых обоснованных принципов. Их можно разделить на три группы:
1) методологические, наиболее общие, обеспечивающие при их применении рациональное поведение экономических субъектов независимо от характера и целей проекта;
2) методические, обеспечивающие экономическую обоснованность оценок эффективности проектов и решений, принимаемых на их основе;
3) операционные, соблюдение которых облегчит и упростит процедуру оценки эффективности проектов и обеспечит необходимую точность расчетов.
Группировка содержательного контента принципов оценки эффективности инвестиций и их распределение указаны в табл. 15.
Т а б л и ц а 15
| № п/п | Методологические | Методические | Операционные |
|---|---|---|---|
| 1 | Измеримость | Сравнение ситуаций с «проектом» и «без проекта» | Взаимосвязь параметров |
| 2 | Сравнимость | Уникальность | Моделирование |
| 3 | Выгодность | Субоптимизация | Организационноэкономический механизм реализации проекта |
| 4 | Согласованность интересов | Неуправляемость прошлого | Многостадийность оценки |
| 5 | Платность ресурсов | Динамичность | Информационная и методическая согласованность |
| 6 | Неотрицательность и максимум эффекта | Временная ценность денег | Симплификация |
| 7 | Системность | Неполнота информации | |
| 8 | Комплексность | Структура капитала | |
| 9 | Неопровергаемость методов | Многовалютность |
Подробное рассмотрение этих принципов содержится во многих научных изданиях по вопросу оценки эффективности инвестиций. Наряду с ними существуют и «частные» принципы, т. е. правила, в соответствии с которыми осуществляются отдельные этапы оценки или учитываются отдельные специфические для конкретного проекта обстоятельства. Такие правила, иногда основанные на практическом опыте или конкретизирующие общие принципы применительно к определенной ситуации, в случае необходимости излагаются при описании соответствующих этапов расчета. Современные методы оценки инвестиций позволяют принимать достаточно обоснованные управленческие решения с минимально возможным уровнем погрешности (ошибок).
Методы оценки реальных инвестиций
В основе процесса принятия управленческих решений инвестиционного характера лежат оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений.
Поскольку сравниваемые показатели относятся к различным моментам времени, ключевой проблемой здесь является их сопоставимость. Воспринимать ее можно по-разному, в зависимости от существующих объективных и субъективных условий: темпа инфляции, размера инвестиций и генерируемых поступлений, горизонта прогнозирования, уровня квалификации аналитика и т. п.
При оценке притока денежных средств по годам может возникнуть проблема в отношении последних лет реализации проекта: чем более протяжен он во времени, тем более неопределенными и рискованными являются притоки денежных средств отдаленных лет. В отношении значений поступлений последних лет могут вводиться понижающие коэффициенты либо эти поступления могут исключаться из анализа.
Наглядным инструментом при анализе инвестиционных проектов является графическое представление соответствующего денежного потока (рис. 21).

В наиболее общем виде инвестиционный проект P представляет собой следующую модель:
P = {Ii, St, n, r}, (11)
где Ii – инвестиции в i-м году; i = 1, 2, ..., m (чаще всего считается, что m = 1);
St – приток (отток) денежных средств в год t; t = 1, 2, ..., n;
n – продолжительность проекта;
r – коэффициент дисконтирования.
При анализе инвестиционных проектов следует учитывать ряд положений:
- с каждым инвестиционным проектом принято связывать денежный поток, элементы которого представляют собой либо чистые оттоки, либо чистые притоки денежных средств, иногда в анализе используется не денежный поток, а последовательность прогнозных значений чистой годовой прибыли, генерируемой проектом;
- чаще всего анализ ведется по годам, хотя его можно проводить по равным базовым периодам любой продолжительности (месяц, квартал). Необходимо при этом увязать величины элементов денежного потока, процентную ставку и длину периода.
- предполагается, что весь объем инвестиций делается в конце года, предшествующего первому году генерируемого проектом притока денежных средств (инвестиции могут быть сделаны в течение ряда последующих лет);
- приток (отток) денежных средств оценивается на конец очередного года.
Методы оценки инвестиционных проектов можно подразделить на следующие группы в зависимости от того, учитывается или нет временный параметр.
1. Методы, основанные на дисконтированных оценках:
- оценки проектов по чистой приведенной стоимости (Net Present Value – NPV);
- расчета индекса чистой доходности (рентабельности) инвестиций (Profitability Index – PI);
- оценки проектов по внутренней норме доходности (Internal Rate of Return – IRR);
- расчета проектов по дисконтированному сроку окупаемости (Discounted Payback Period – DPP).
2. Методы, основанные на учетных оценках:
- оценки проектов по сроку окупаемости (Payback Period – PP);
- расчета дохода (прибыли) от инвестиций (Return on investment – ROI);
- оценки проектов по бухгалтерской норме доходности (коэффициент эффективности инвестиций) (Accounting Rate of Return – ARR).
Метод оценки проектов по чистой приведенной стоимости (Net Present Value – NPV)
Этот метод основан на сопоставлении величины исходной инвестиции I0 с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока.
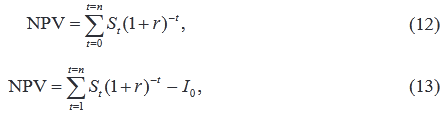
где St – поток реальных денег в год t (приток имеет знак «+», отток – знак «–»), ден. ед.;
n – срок действия проекта (горизонт расчета), годы;
r – ставка дисконта (относительные единицы);
I0 = S0 – первоначальные инвестиции, ден. ед.
Коэффициент 1/(1+t)t называется коэффициентом дисконтирования (или дисконтированным множителем).
NPV следует рассматривать как приведенный к моменту начала реализации проекта экономический эффект от его функционирования.
Проект может быть принят к реализации, если его NPV > 0.
Из двух проектов выбирают тот, который характеризуется наибольшей чистой приведенной стоимостью NPV.
NPV – это критерий аддитивный, т. е. NPV(А + В) = NPV(А) + NPV(В).
Следовательно, NPV совокупности проектов равна сумме NPV каждого проекта.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение m лет, то формула для расчета NPV модифицируется следующим образом:
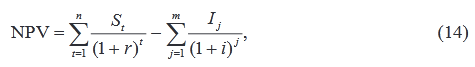
где i – прогнозируемый средний уровень инфляции.
Метод расчета индекса чистой доходности (рентабельности) инвестиций (Profitability Index – PI)
Индекс чистой доходности используют при выборе инвестиционного проекта из нескольких имеющихся альтернативных проектов:

где PI – относительный показатель, который характеризует уровень доходов на единицу затрат, т. е. экономическую эффективность инвестиций. Условие выбора варианта PI -> max.
В числителе дроби выражения (15) указана чистая приведенная стоимость плюс непосредственно стоимость проекта (первоначальные инвестиции).
Метод оценки проектов по внутренней норме доходности (окупаемости) (Internal Rate of Return – IRR)
Метод внутренней нормы доходности использует концепцию дисконтированной стоимости. Он сводится к нахождению такой ставки дисконтирования, при которой текущая стоимость ожидаемых от инвестиционного проекта доходов будет равна текущей стоимости необходимых денежных вложений. Иными словами, IRR – это значение коэффициента дисконтирования, при котором NPV = 0.
Внутренняя норма доходности IRR находится путем решения относительно

Решение уравнения производится методом итераций.
Проект может быть принят, если IRR превышает величину существующей учетной ставки (используемой при расчете NPV) или равен ей.
Для более наглядного понимания природы критерия IRR воспользуемся графическим методом (рис. 22).
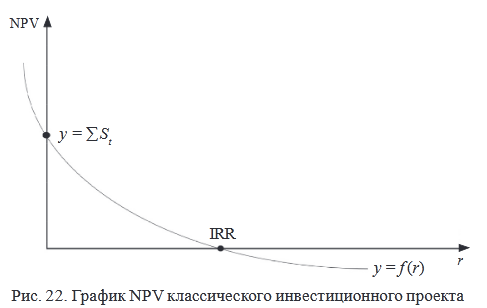
Рассмотрим функцию

Эта функция имеет ряд свойств:
1) y = f(r) – нелинейная функция; это свойство может иметь серьезные последствия при расчете критерия;
2) при r = 0 выражение в правой части преобразуется в сумму элементов исходного денежного потока, т. е. график NPV пересекает ось ординат в точке, равной сумме всех элементов дисконтированного денежного потока, включая величину исходных инвестиций;
3) для проекта с обычным денежным потоком (отток сменяется притоком) функция y = f(r) является убывающей, т. е. с ростом r график функции стремится к оси абсцисс и пересекает ее в точке IRR;
4) ввиду нелинейности функции y = f(r), а также возможных различных комбинаций знаков элементов денежного потока, функция может иметь несколько точек пересечения с осью абсцисс.
Смысл расчета внутренней нормы доходности при анализе эффективности планируемых инвестиций заключается в следующем: IRR показывает ожидаемую доходность проекта и, следовательно, максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом.
Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.
В качестве критерия сравнения может использоваться средневзвешенная стоимость капитала при условии, что предприятие использует несколько источников финансирования инвестиционного проекта.
Практическое применение данного метода осложняется, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием коэффициентов дисконтирования. Для этого с помощью таблиц выбираются два коэффициента дисконтирования r1 < r2 таким образом, чтобы в интервале (r1,r2) функция NPV = f(r) меняла свое значение с «+» на «–» или с «–» на «+». Далее применяют формулу
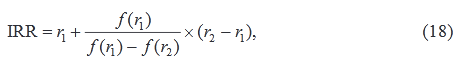
где r1 – значение табулированного коэффициента дисконтирования, при котором f(r1) > 0; (f (r1) < 0);
r2 – значение табулированного коэффициента дисконтирования, при котором f(r2) < 0; (f (r2) > 0);
точность вычислений обратно пропорциональна длине интервала (r1,r2), а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала равна 1 %, т. е. r1, r2 – ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции у = f(r) с «+» на «–»);
r1 – значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV;
r2 – значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV.
Сравнительная характеристика критериев NPV и IRR
Основным недостатком метода IRR является предположение, что поступающие денежные потоки реинвестируются по ставке r = IRR проекта. Использование критерия NPV предполагает, что доступной процентной ставкой, по которой могут быть реинвестированы поступающие денежные средства, является цена капитала. Таким образом, по критерию NPV дисконтирование выполняется по цене капитала, тогда как по критерию IRR – по величине IRR проекта. Однако доступной и возможной ставкой реинвестирования является цена капитала. Этим обосновывается предпочтительность критерия NPV.
Рассмотрим некоторые особенности использования методов NPV и IRR.
1. Альтернативные проекты, различающиеся по масштабу
В сравнительном анализе альтернативных инвестиционных проектов критерий IRR можно использовать достаточно условно. Так, если расчет критерия IRR для двух проектов показал, что его значение для проекта А больше, чем для проекта В, то чаще всего проект А может рассматриваться как более предпочтительный, поскольку допускает большую гибкость в варьировании источниками финансирования инвестиций, цена которых может существенно различаться. Однако такое предпочтение носит весьма условный характер. Поскольку IRR является относительным показателем, на его основе невозможно сделать правильные выводы об альтернативных проектах с позиции их возможного вклада в увеличение капитала фирмы, особенно если проекты существенно различаются по масштабу (т. е. величине инвестиций).
П р и м е р 1
Проанализируем два альтернативных проекта, если цена капитала компании составляет 10 %. Исходные данные и результаты расчетов приведены в табл. 16.
Т а б л и ц а 16
| Проект | Величина инвестиций | Денежный поток | IRR, % | NPV, при 10 % | |
|---|---|---|---|---|---|
| 1-й год | 2-й год | ||||
| А | 250 | 150 | 700 | 100 | 465 |
| В | 15 000 | 5 000 | 19 000 | 30,4 | 5 248 |
Фирма может отдать предпочтение проекту А с более высоким значением IRR. Однако из-за небольшого объема первоначальных инвестиций проект А дает небольшой доход (на порядок меньше, чем проект В). Поэтому, если фирма имеет возможность профинансировать проект В, его следует предпочесть.
2. Резерв безопасности проекта
Основной недостаток критерия NPV в том, что это абсолютный показатель, поэтому он не может дать информации о так называемом резерве безопасности проекта. Возникает вопрос: если допущена ошибка в прогнозе денежного потока или коэффициента дисконтирования, насколько велика опасность того, что проект, который ранее рассматривался как прибыльный, окажется убыточным?
Информацию о резерве безопасности дают критерии IRR и PI. Так, при прочих равных условиях:
- чем больше IRR по сравнению с ценой капитала проекта, тем больше резерв безопасности;
- чем более значение PI превосходит единицу, тем больше резерв безопасности.
Иными словами, с позиции риска можно сравнивать два проекта по критериям IRR и PI, но нельзя по критерию NPV.
Рассмотрим следующую ситуацию.
П р и м е р 2
Проект С имеет прогнозные значения денежного потока, млн долл.: –100; 20; 25; 40; 70. Требуется проанализировать целесообразность включения его в инвестиционный портфель при условии, что цена капитала r = 15 %.
Расчеты показывают, что NPVC = 2,6 млн долл. Можно сделать вывод, что проект обеспечивает высокий прирост капитала компании (в абсолютном выражении).
Однако IRRC = 16 %, т. е. очень близко к прогнозируемой цене капитала.
Очевидно, что проект С является весьма рисковым.
Если предположить, что в оценке прогнозируемой цены источника допущена ошибка и реальное ее значение r = 17 %, проект С принять нельзя, так как NPVC = –2,3 млн долл.
Данный пример показывает, что ориентация на критерий NPV не всегда оправдана. Высокое значение NPV может быть сопряжено с достаточно высоким риском.
Высокое значение IRR во многих случаях указывает на наличие определенного резерва безопасности в отношении данного проекта.
3. Альтернативные проекты, различающиеся по интенсивности притока денежных средств
Противоречие между NPV и IRR может также возникать из-за различий в распределении общей суммы притока денежных средств во времени, даже если два проекта имеют одинаковую величину исходных инвестиций.
Кроме того, поскольку зависимость NPV от ставки дисконтирования r нелинейная, значение NPV может существенно зависеть от r, причем степень этой зависимости различна и также определяется динамикой элементов денежного потока.
П р и м е р 3
Рассмотрим два независимых проекта, млн рублей.
А: –200; 150; 80; 15; 15; 10;
В: –200; 20; 50; 50; 90; 110.
Требуется ранжировать их по степени приоритетности при условии, что планируемая цена источника финансирования весьма неопределенна и может варьировать в интервале от 5 до 20 %. В табл. 17 приведены результаты расчетов для различных возможных ситуаций.
Т а б л и ц а 17
| Проект | Значение NPV при | IRR | |||
|---|---|---|---|---|---|
| r = 5 | r = 10 | r = 15 | r = 20 | ||
| А | 48,6 | 30,2 | 14,3 | 0,5 | 20,2 |
| В | 76,5 | 34,3 | 0,7 | –26,3 | 15,1 |
Проекты А и В не одинаковым образом реагируют на изменение значения коэффициента дисконтирования. Причина – проект А имеет убывающий денежный поток, проект В – нарастающий. Поскольку интенсивность возмещения инвестиции в проекте А существенно выше, чем в проекте В, он в меньшей степени реагирует на негативное увеличение коэффициента дисконтирования.
Анализируя проекты при различных значениях коэффициента дисконтирования, можно сделать вывод, что при r = 5 % по критерию NPV наиболее предпочтительным является проект В, а по критерию IRR – проект А. Однако при увеличении r до 20 % и по критерию NPV, и по критерию IRR предпочтение следует отдать проекту А.
Судя по значению IRR, проект В является более рискованным.
4. Влияние коэффициента дисконтирования на ранжирование проектов по критерию NPV
Для проектов классического характера (с ординарным денежным потоком) критерий IRR показывает лишь максимальный уровень затрат, который может быть ассоциирован с оцениваемым проектом. Если цена инвестиций в оба альтернативных проекта меньше, чем значение IRR для них, выбор может быть сделан с помощью дополнительных критериев. Критерий IRR не позволяет различить ситуации, когда цена капитала меняется.
П р и м е р 4
В табл. 18 приведены исходные данные по двум альтернативным проектам. Требуется выбрать один из них при условии, что цена капитала, предназначенного для инвестирования проекта А – 8 %; Б – 15 %.
Исходя из критерия IRR, оба проекта равноправны. На первый взгляд, сделать выбор невозможно. Построим графики функции NPV = f(r) для обоих проектов (рис. 23).
На рис. 23 видно, что с ростом r графики NPV проектов А и В убывают.
Т а б л и ц а 18
| Проект | Величина инвестиции | Денежный поток по годам | IRR, % | Точка Фишера | |||
|---|---|---|---|---|---|---|---|
| 1-й | 2-й | 3-й | r, % | NPV | |||
| А | –100 | 90 | 45 | 30 | 9,82 | 9 | 26,06 |
| В | –100 | 10 | 50 | 20,4 | 9,82 | 100 | 26,06 |
| А – В | 0 | –80 | 5 | 9,82 | – | 91 | – |
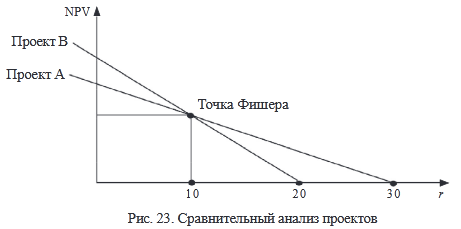
Заметим, что проект В имеет более высокое значение NPV при низких значениях r; при r > 9,8 % проект А имеет более высокие значения NPV.
Можно сделать вывод, что NPV проекта В «более чувствителен» к изменению ставки дисконта, чем NPV проекта А, поскольку с ростом r NPVB убывает более высокими темпами. Это связано с тем, что приток денежных средств в проекте А идет более быстрыми темпами. Если проект имеет большую часть поступлений в начальные годы, его NPV с ростом r будет убывать значительно медленнее по сравнению с проектом, в котором в первые годы поступает относительно меньшая часть общего притока денежных средств.
Следовательно, проект В, который имеет большую часть поступлений, в последние годы невыгоден, если дисконтная ставка повышается, тогда как проект А, в котором приток денежных средств идет более быстрыми темпами в первые годы, в меньшей степени реагирует на увеличение ставки.
Точка пересечения двух графиков (r = 9,82 %), показывающая значение коэффициента дисконтирования, при котором оба проекта имеют одинаковый NPV, называется точкой Фишера. Она служит пограничной точкой. Исходя из этого, можно сделать вывод, что в случае а) следует предпочесть проект А; в случае б) – проект В.
Точка Фишера для потоков А и В может быть найдена как IRR разностного потока (А – В) или (В – А).
5. Свойство аддитивности
Одним из существенных недостатков критерия IRR является то, что, в отличие от критерия NPV, он не обладает свойством аддитивности, т. е. для двух инвестиционных проектов А и В, которые могут быть осуществлены одновременно:
NPV(A + B) = NPV(A) + NPV(B), но IRR(A + B) = IRR(A) + IRR(B).
6. Множественность IRR
Критерий IRR совершенно непригоден для анализа неординарных инвестиционных потоков. В этом случае может возникнуть множество значений IRR, возможны ситуации, когда положительного значения IRR не существует (рис. 24).
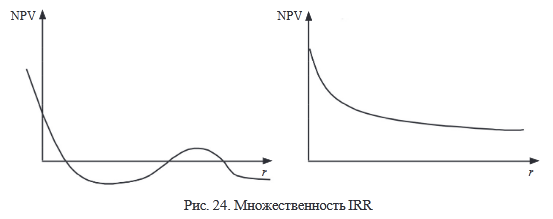
Рис. 24. Множественность IRR
7. Сложность вычисления
С точки зрения процедуры вычисления, вычисление IRR значительно сложнее, чем NPV.
Модифицированная внутренняя норма доходности (Modified Internal Rate of Return – MIRR).
Основной недостаток, присущий IRR, в отношении оценки проектов с неординарными денежными потоками, не является критическим и может быть преодолен.
Соответствующий аналог IRR, который может применяться при анализе любых проектов, назвали модифицированной внутренней нормой прибыли (MIRR).
Алгоритм расчета MIRR:
1. Рассчитывается суммарная дисконтированная стоимость всех оттоков по цене источника финансирования проекта.
2. Рассчитывается суммарная наращенная стоимость всех притоков по цене источника финансирования проекта – терминальная стоимость.
3. Определяется коэффициент дисконтирования, который уравнивает суммарную приведенную стоимость оттоков и терминальную стоимость, т. е. MIRR.
Общая формула расчета имеет вид:
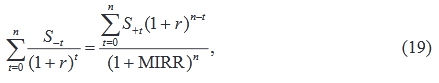
где S–t – отток денежных средств в период t (по абсолютной величине);
S+t – приток денежных средств в период t;
r – цена источника финансирования данного проекта;
n – продолжительность проекта.
Формула имеет смысл, если терминальная стоимость превышает сумму дисконтированных оттоков. Критерий MIRR всегда имеет единственное значение, поэтому может применяться вместо критерия IRR для неординарных потоков.
Противоречия между критериями NPV и MIRR могут возникать, если проекты различаются по масштабу:
- значения элементов у одного потока значительно больше по абсолютной величине, чем у другого;
- проекты имеют различную продолжительность.
Методы определения срока окупаемости инвестиций (Payback Period – PP)
Срок (период) окупаемости – один из самых простых и наиболее часто используемых методов оценки инвестиций. Он не предполагает временной упорядоченности денежных поступлений.
Период окупаемости (payback period) определяется как время, требуемое для того, чтобы доходы от инвестиционного проекта стали равны первоначальному вложению в данный проект.
Если ожидается, что денежный поток от инвестиционного проекта будет одинаковым в течение ряда лет, то
| Tок = | I0 | , лет, (20) |
| S+t |
где I0 – первоначальные инвестиции;
St – ежегодный поток реальных денег.
Если ожидаемый поток доходов меняется из года в год, необходимо составить баланс денежных потоков (кумулятивный денежный поток).
Tок находится по выражению:

где t' – номер года, в котором сумма денежных потоков поменяла знак (стала положительной);
ΣSt – баланс (сумма) денежных потоков;
S't – в знаменателе – денежный поток, который изменил знак с «–» на «+».
П р и м е р 5
Проект генерирует следующие денежные потоки, тыс. рублей:
С0 = –100; С1 = +50; С2 = –20; С3 = +30; С4 = +60; С5 = +40.
Составляем баланс (кумулятивный денежный поток), тыс. рублей:
0-й год – (–100);
1-й год – (–50);
2-й год – (–70);
3-й год – (–40);
4-й год – (+20).
Tок = 3,67 года.
Недостатки метода:
- не рассматривает доходы от инвестиций за пределами периода окупаемости;
- не учитывает разницу во времени получения доходов в пределах периода окупаемости;
- не учитывает различие в распределении доходов по годам;
- не позволяет судить об экономической выгоде проекта;
- не учитывает различие в первоначальных инвестициях разных проектов.
Преимущества метода:
- очень прост;
- позволяет судить о ликвидности проекта (главное, чтобы инвестиции окупались и как можно скорее);
- дает представление об уровне риска проекта (чем короче срок окупаемости, тем менее рискованным является проект).
Дисконтированный период окупаемости
Это период времени, необходимый для того, чтобы текущая стоимость из отрицательной стала положительной. Используя данный метод, мы находим точку безубыточности проекта. Денежные потоки дисконтируются по показателю «средневзвешенная цена капитала», и рассчитывается сумма
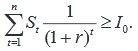
Дальнейший расчет аналогичен расчету обычного периода окупаемости.
В случае дисконтирования срок окупаемости увеличивается, т. е. проект, приемлемый по критерию срока окупаемости, может оказаться неприемлемым по критерию дисконтированного срока окупаемости.
Метод расчета доходности инвестиций (Return of Investment – ROI)
Данный метод предусматривает сопоставление ежегодной прибыли (до налогообложения или после) с первоначальными капиталовложениями.
Существует несколько форм такого сопоставления. Предполагается, что срок функционирования проекта известен.
а. Ежегодная прибыль от полных первоначальных капиталовложений
| ROI = | Ежегодная прибыль | = | St | , (22) |
| Первоначальные капиталовложения | I0 |
б. Ежегодная прибыль от средних за период функционирования проекта капиталовложений
| ROI = | St | , (23) |
| (I0±Iкон)/2 |
где Iкон – остаточная или ликвидационная стоимость проекта.
в. Среднегодовая прибыль от средних капиталовложений за период T

Может быть использован и следующий подход при расчете ROI: сопоставление ежегодной прибыли (до налогообложения или после) с первоначальными капиталовложениями.

где
числитель – средняя прибыль за период функционирования проекта (расчет ведется начиная с первого года функционирования проекта);
Pt – прибыль в год t;
Т – количество периодов функционирования проекта;
знаменатель – средние инвестиции (если капитальные вложения осуществляются в течение нескольких периодов, они суммируются и усредняются по количеству периодов инвестирования);
In – инвестиции в период n;
N – количество периодов инвестирования.
Достоинства метода:
- простота;
- широкое использование на практике.
Недостатки метода:
- метод не учитывает временную компоненту денежных потоков, денежные потоки не дисконтируются;
- не учитывается время поступления денежных потоков, формирующих прибыль. Для инвестора предпочтительнее проекты, которые дают большие притоки реальных денег в начале периода;
- метод не учитывает разницу между проектами, имеющими одинаковую среднегодовую прибыль, но генерируемую в течение различного количества лет;
- величина ROI подсчитывается по балансовой стоимости активов, хотя для инвестора важен показатель, отражающий их рыночную стоимость.
Метод оценки проектов по бухгалтерской норме доходности (Accounting Rate of Return – ARR)
Этот показатель используется менеджерами как показатель эффективности функционирования. В самом общем виде он определяется следующим образом:
| ARR = | Средняя бухгалтерская прибыль |
| Среднее значение капиталовложений |
Здесь средняя бухгалтерская прибыль – это среднегодовая прибыль после уплаты налогов за весь период функционирования проекта.
Среднее значение капиталовложений также относится ко всему периоду функционирования проекта.
Однако поскольку речь идет об использовании при расчетах информации, содержащейся в бухгалтерских документах, рассматриваемый показатель для какого-то года t можно представить в виде:
| ARR = | Ft - (At-1 - At) | , (26) |
| At-1 |
где Ft – чистый (после налога) приток реальных денег в год t;
At – балансовая стоимость материальных активов в год t.
Очевидно, что разность (At–1 – At) представляет собой амортизацию основных фондов за год.
За весь период функционирования проекта Т величина показателя находится как средняя величина:

Решения, связанные с инвестициями, имеют для фирмы исключительно большое значение. Поэтому для их принятия нельзя пользоваться каким-то одним методом анализа альтернативных инвестиционных предложений. Следует использовать все методы, тщательно проанализировать причины возникающих расхождений в порядках ранжирования.
Наиболее весомым считается метод NPV. Однако возможна ситуация, когда значения NPV для нескольких проектов одинаковы или очень близки. Тогда целесообразно оценить их с помощью других методов.
Методы оценки финансовых инвестиций
Природа ценных бумаг делает инвестирование в них не похожим на инвестирование в основные фонды. Это отличие обусловлено следующими обстоятельствами:
- возможностью деления этих инвестиций на мелкие части;
- возможностью осуществлять вложения средств на короткие промежутки времени.
Благодаря этому при инвестициях в ценные бумаги можно не принимать во внимание объемы и длительности периодов инвестирования альтернативных вариантов.
Из-за очень большого числа инвесторов на рынке ценных бумаг использование для анализа эффективности вариантов метода NPV невозможно.
Для оценки доходности инвестиций в ценные бумаги можно использовать показатель нормы доходности за период владения ценной бумагой HPR (holding period return).
Идея заключается в том, чтобы определить период владения основным капиталом, после чего допустить, что любые выплаты, полученные за период, реинвестировали.
Принято считать, что любая выплата, полученная по ценной бумаге (например, дивиденд по акции), используется для дальнейшего приобретения ценных бумаг по текущему рыночному курсу.
Для периода в один год:
| HPR = rhp = | Vt | -1, |
| Vt-1 |
где Vt – стоимость на конец периода владения;
Vt-1 – стоимость на начало периода владения.
Доходность за период владения rhp можно преобразовать в эквивалентную доходность за единичный период rg:
(1 + rg)N = 1 + rhp
или
rg = (1 + rhp)1/N – 1,
где N – количество единичных промежутков за период владения.
П р и м е р
Акции в начале первого года стоят $ 46 за штуку. Они принесли за год дивиденды в размере $ 1,5. В конце первого года акции стоили $ 50 и принесли в следующем году дивиденды в размере $ 2. К концу второго года акции котировались по курсу $ 56. Какова доходность акций за период владения в два года?
Относительная стоимость для двухгодичного периода владения будет равна: 1,1196 × 1,16 = 1,2987.
Относительная стоимость каждого периода можно рассматривать как [1 + доходность] за этот период.
В нашем примере: доходность за первый год – 11,96 %; второй год – 16 %.
Доходность за два года – 29,87 %. Годовая доходность: 13,96 %.
Если речь идет об N-периодах:
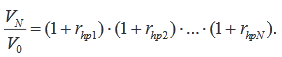
Чтобы преобразовать полученный результат в доходность за время владения в расчете на один период с учетом начисления сложных процентов, можно вычислить среднегеометрическую доходность за отдельные периоды:
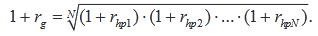
Таким образом, показатель нормы доходности ценной бумаги для периода, состоящего из N лет, определяется по выражению:
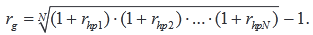
Платежи по безрисковым ценным бумагам могут быть предсказаны, так как их размеры и распределение по срокам точно известны.
Проблема выбора инвестиционного портфеля
В 1952 г. Гарри Марковиц опубликовал фундаментальную работу, которая является основой подхода к инвестициям с точки зрения современной теории формирования портфеля. Подход Марковица к проблеме выбора портфеля предполагает, что инвестор старается решить две проблемы:
- максимизировать ожидаемую доходность при заданном уровне риска;
- минимизировать неопределенность (риск) при заданном уровне ожидаемой доходности.
Следствием наличия двух противоречивых целей является необходимость проведения диверсификации с помощью покупки не одной, а нескольких ценных бумаг.
Доходность ценной бумаги за один период может быть вычислена по формуле:
Доходность = (Благосостояние в конце периода – Благосостояние в начале периода) / Благосостояние в начале периода.
Благосостояние в начале периода – цена покупки одной ценной бумаги данного вида в момент t = 0.
Благосостояние в конце периода – рыночная стоимость данной ценной бумаги в момент t = 1 в сумме со всеми выплатами держателю данной бумаги.
Поскольку портфель представляет собой совокупность различных ценных бумаг, его доходность может быть вычислена следующим образом:
| rp = | W1 - W0 | , |
| W0 |
где W0 – совокупная цена покупки всех ценных бумаг, входящих в портфель в момент t = 0;
W1 – совокупная рыночная стоимость этих ценных бумаг в момент t = 1 в сумме с совокупным денежным доходом от обладания ценными бумагами с момента t = 0 до момента t = 1. Отсюда
W0(1 + rp) = W1.
По Марковицу, инвестор должен считать уровень доходности, связанный с любым из альтернативных портфелей случайной переменной.
Норма доходности имеет две характеристики:
- математическое ожидание нормы доходности портфеля финансовых активов;
- дисперсия/ стандартное отклонение нормы доходности портфеля.
Математическое ожидание нормы доходности портфеля:
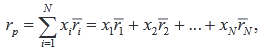
где xi – доля начальной стоимости портфеля, инвестированная в ценную бумагу i (доля актива i в инвестициях всего портфеля);
ri – математическое ожидание доходности ценной бумаги i.
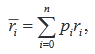
где ri – норма доходности при исходе i, i ∈ 1,n;
pi – вероятность исхода i.
П р и м е р 1. Вычисление ожидаемой доходности портфеля.
а. Стоимость ценной бумаги и портфеля:
| Наименование ЦБ | Количество акций в портфеле | Начальная рыночная цена одной акции, $ | Cумма инвестиций, $ | Доля в начальной рыночной стоимости портфеля |
|---|---|---|---|---|
| А | 100 | 40 | 4 000 | 4 000/17 200 = 0,2325 |
| В | 200 | 35 | 7 000 | 7 000/17 200 = 0,4070 |
| С | 100 | 62 | 6 200 | 6 200/17 200 = 0,3605 |
Начальная стоимость портфеля W0 = $ 17 200. Сумма долей = 1,0.
б. Вычисление ожидаемой доходности портфеля с использованием стоимости на конец периода:
| Наименование ЦБ | Количество акций в портфеле | Ожидаемая стоимость одной акции в конце периода, $ | Совокупная ожидаемая стоимость в конце периода, $ |
|---|---|---|---|
| А | 100 | 46,48 | 46,48×100 = 4648 |
| В | 200 | 43,61 | 43,61×200 = 8722 |
| С | 100 | 76,14 | 76,14×100 = 7614 |
Ожидаемая стоимость портфеля в конце периода Wi = $ 20 984.
Ожидаемая доходность портфеля rp 22 %.
в. Вычисление ожидаемой доходности портфеля с использованием ожидаемой доходности ценных бумаг:
| Наименование ЦБ | Доля в начальной рыночной стоимости | Ожидаемая доходность ценных бумаг, % | Вклад в ожидаемую доходность портфеля, % |
|---|---|---|---|
| А | 0,2325 | 16,2 | 0,2325×16,2 = 3,77 |
| В | 0,407 | 24,6 | 0,4070×22,8 = 8,22 |
| С | 0,3605 | 22,8 | 0,3605×22,8 = 8,22 |
Ожидаемая доходность портфеля rp 22 %.
Дисперсия / стандартное отклонение нормы доходности портфеля
Дисперсия доходности одной ценной бумаги i – это математическое ожидание квадрата разницы между ri и ri:
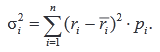
Дисперсия нормы доходности портфеля:
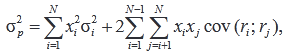
где cov (ri; rj) – ковариация между нормами доходности активов i и j.
Ковариация – это статистическая характеристика, иллюстрирующая меру сходства (или различия) двух ценных бумаг. Она показывает, как доходности двух ценных бумаг i и j зависят друг от друга.
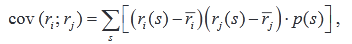
где s – событие.
Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону (лучшая, чем ожидаемая доходность одной из ценных бумаг сопровождается лучшей, чем ожидаемая, доходностью другой ценной бумаги). Отностительно небольшое или нулевое значение ковариации показывает, что связь между доходностью этих ценных бумаг слаба или отсутствует.
cov (ri; rj) = ρijσiσj,
где ρij – коэффициент корреляции между ri и rj;
σi и σj – стандартные отклонения.
Коэффициент корреляции нормирует ковариацию для облегчения сравнения с другими парами случайных переменных и принимает значения от –1 до +1.
Для двух ценных бумаг:
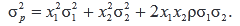
Рассмотрим различные варианты корреляции между доходностями двух ценных бумаг (рис. 25).
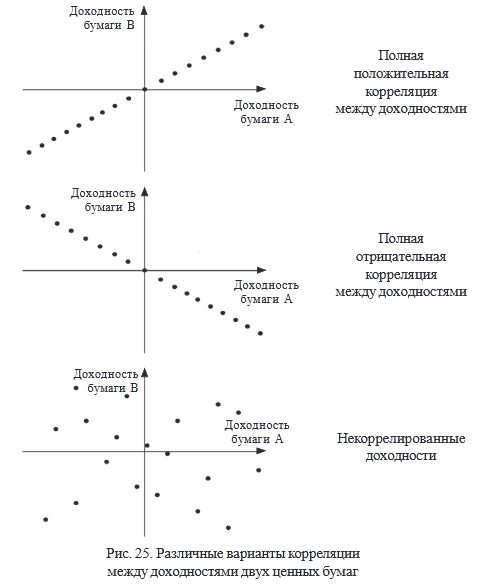
Если ρ = –1 – ценные бумаги, r1 и r2 находятся в отрицательной линейной зависимости (при увеличении r1 r2 уменьшается на точно известную величину).
Если ρ > 0 – корреляция положительна, но значение r1 не позволяет предсказать точную величину r2.
Рассмотрим различные значения ρ.
1. ρ = 1 – линейная зависимость доходности активов А и В.
Ожидаемая доходность портфеля (рис. 26):
rp = x1r1 + x2r2
где x1 – доля инвестиций в актив 1;
x2 – доля инвестиций в актив 2.
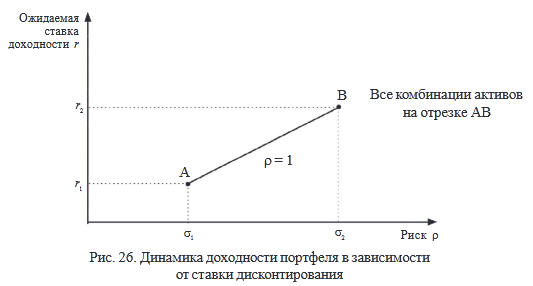
Среднеквадратическое отклонение доходности портфеля рассчитывается по формуле:
σp = x1σ1 + x2σ2 – упрощенное выражение, которое может быть использовано лишь при ρ = –1 – отрицательная линейная зависимость. График безрискового портфеля представлен на рис. 27.
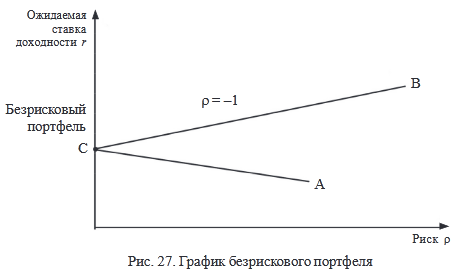
2. ρ = –1 – отрицательная линейная зависимость.
При ρ = –1 можно составить такой портфель, риск которого будет нулевым.
Если портфель на 100 % состоит из актива вида В, мы находимся в точке В.
По мере того, как мы заменяем часть активов В на А, и риск, и ожидаемая доходность снижаются до тех пор, пока не достигнута точка С. При включении в портфель все больше активов типа А риск увеличивается, доходность падает.
Кривые безразличия
Метод, который применяется для выбора наиболее желательного портфеля, использует так называемые кривые безразличия инвестора (рис. 28). Эти кривые отражают отношение инвестора к риску и доходности и представляют собой различные комбинации риска и доходности, которые инвестор считает равноценными.
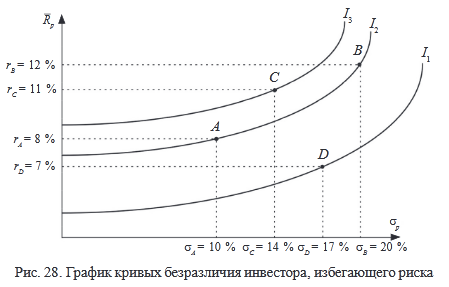
Инвестор будет считать портфели А и В равноценными, несмотря на то, что они имеют различные ожидаемые доходности и стандартные отклонения, так как оба эти портфеля лежат на одной кривой безразличия I2.
Кривые безразличия не могут пересекаться. Чтобы доказать это условие, предположим, что кривые безразличия пересекаются (рис. 29).
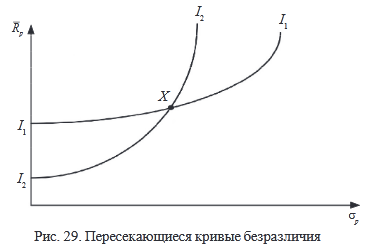
На рис. 29 точка пересечения обозначена Х. Все портфели на кривой являются равноценными. Это означает что все они так же ценны, как и Х, потому что Х находится на I1. Все портфели на I2 является равноценными и в то же время такими же ценными, как и Х, потому что Х также принадлежит кривой I2. Исходя из того, что Х принадлежит кривым безразличия, все портфели на I1 должны быть настолько же ценны, насколько и все портфели на I2. Но это приводит к противоречию, потому что I1 и I2 являются двумя различными кривыми, отражающими различные уровни желательности.
Вернемся к рис. 26. Инвестор найдет портфель С с ожидаемой доходностью 11 % и стандартным отклонением 14 %, более предпочтительным по сравнению с А и В. Это объясняется тем, что портфель С лежит на кривой безразличия I3, которая расположена выше и левее, чем I2.
Это приводит к следующему свойству кривых безразличия:
* инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее.
Инвестор имеет бесконечное число кривых безразличия. Это означает, что как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними.
При использовании подхода Марковица делается предположение о ненасыщаемости, т. е. предполагается, что инвестор предпочитает более высокий уровень конечного благосостояния более низкому его уровню.
Второе предположение заключается в том, что инвестор избегает риска.
Степень избегания рисков у различных инвесторов неодинакова (рис. 30).
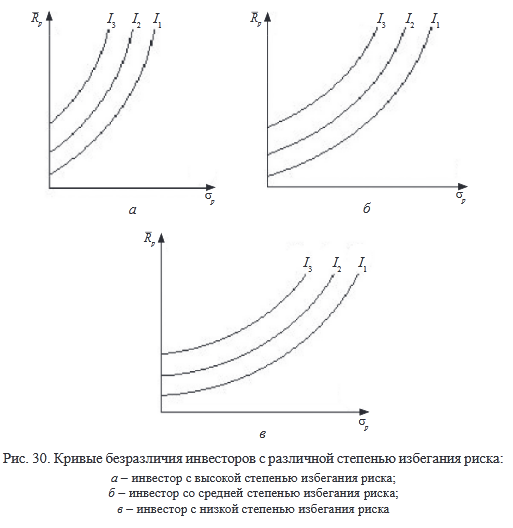
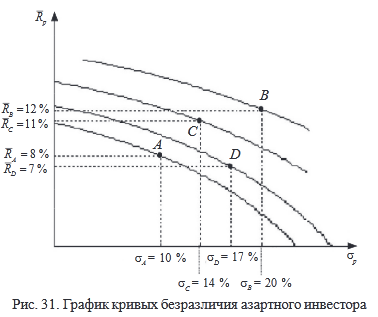
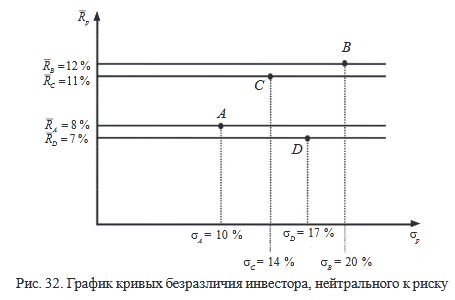
Предположение Марковица о том, что инвестор избегает риска, не является необходимым. Можно предположить, что инвестор азартен (рис. 31) или нейтрален к риску (рис. 32).
Портфельный анализ
Из набора N ценных бумаг можно сформировать бесконечное число портфелей. Инвестор не должен проводить оценку всех этих портфелей. Существует теорема об эффективном множестве, которая объясняет тот факт, что инвестор должен рассмотреть только подмножество возможных портфелей.
Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых:
- Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска.
- Обеспечивает минимальный риск для некоторого значения ожидаемой доходности.
Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством, или эффективной границей.
Рис. 33 представляет иллюстрацию местоположения достижимого множества (или множества возможностей), из которого может быть выделено эффективное множество.
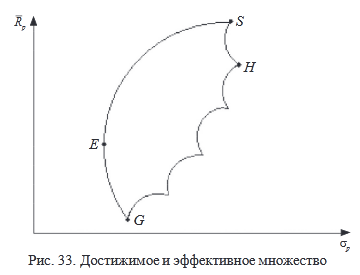
Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. Все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе (например E, S, H, G), либо внутри достижимого множества.
В общем случае данное множество будет иметь форму типа зонта.
Применив теорему об эффективном множестве к достижимому множеству, можно определить местоположение эффективного множества.
1. Выделим множество портфелей, удовлетворяющих первому условию теоремы. Не существует менее рискового портфеля, чем портфель E и более рискового, чем портфель H. Таким образом, множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества, расположенная между точками E и H.
2. Выделим множество портфелей, удовлетворяющих второму условию теоремы. Не существует портфеля, обеспечивающего большую ожидаемую доходность, чем портфель S, и меньшую ожидаемую доходность, чем портфель G. Таким образом, множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества, расположенная между точками S и G.
Нас удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества между точками E и S – эффективное множество. Из этого множества инвестор будет выбирать оптимальный для себя портфель (рис. 34). Инвестор должен совместить свои кривые безразличия с эффективным множеством.
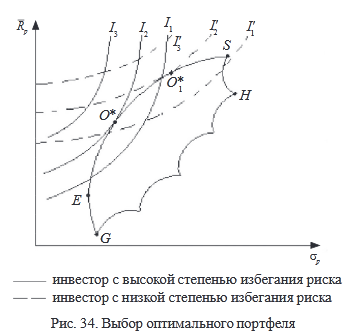
Оптимальный портфель О*, который находится в точке касания кривой безразличия эффективного множества.
Модель оценки финансовых активов
Ожидаемая доходность актива должна быть увязана со степенью рискованности этого актива, которая измеряется коэффициентом β – «бета».
Точный характер этой зависимости показан в модели САРМ – модели оценки финансовых активов (Capital Asset Pricing Model). Модель САРМ служит теоретической основой ряда различных методов, применяемых в инвестиционной практике.
Модель САРМ основывается на некоторых предположениях:
- Инвесторы производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и стандартных отклонениях за период владения.
- Инвесторы никогда не бывают пресыщенными. При выборе между двумя портфелями они предпочтут тот, который при прочих равных условиях дает наибольшую ожидаемую доходность.
- Инвесторы не желают рисковать. При выборе между двумя портфелями они предпочтут тот, который при прочих равных условиях имеет наименьшее стандартное отклонение.
- Частные активы бесконечно делимы. При желании инвестор может купить часть акций.
- Существует безрисковая ставка процента, по которой инвестор может дать взаймы (т. е. инвестировать) или взять в долг денежные средства.
- Налоги и операционные издержки несущественны.
Приведенные выше предположения дополняются следующими:
- Для всех инвесторов период владения одинаков.
- Безрисковая процентная ставка одинакова для всех инвесторов.
- Информация доступна для всех инвесторов.
- Инвесторы имеют одинаковые ожидания, т. е. они одинаково оценивают ожидаемые доходности, среднеквадратичные отклонения и ковариации доходностей ценных бумаг.
Как следует из этих предположений, в САРМ рассматривается предельный случай: все инвесторы обладают одной и той же информацией и по одинаковому оценивают перспективы ценных бумаг. При этом рынки ценных бумаг являются совершенными рынками: в них нет факторов, которые бы препятствовали инвестициям.
Такие потенциальные препятствия, как ограниченная делимость, налоги, операционные издержки и различие между ставками безрискового заимствования и кредитования считаются отсутствующими.
В модели САРМ определяется связь между риском и доходностью эффективных портфелей. Это представлено на рис. 35.
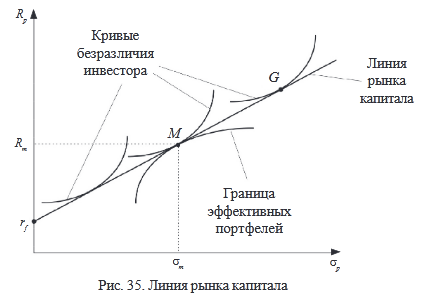
Точка М обозначает рыночный портфель, rf – безрисковая ставка доходности.
Эффективные портфели находятся вдоль прямой, которая получила название «линия рынка капитала» CML (capital market line).
Уравнение CML имеет вид:
Rp = arf + (1 – a)Rm,
σp = (1 – a)σm,
где a – доля безрисковых ценных бумаг в портфеле;
Rm, σm – доходность и среднеквадратичное отклонение рыночного портфеля;
Rp, σp – доходность и среднеквадратичное отклонение эффективного портфеля.
Это уравнение может быть преобразовано следующим образом:

Свойства линии (CML):
- наклон CML равен единице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги (Rm – rf), деленной на разницу их рисков (σm – 0)
- функция Rp = f(σp) – линейная функция.
- на линии CML расположены все эффективные портфели.
- в случае равновесия на рынке ценных бумаг все инвесторы в точке М будут стремиться иметь портфели, одинаковые по относительному составу ценных бумаг.
- Rp увеличивается при увеличении в портфеле ценных бумаг с повышенным риском.
Ординату точки пересечения CML с вертикальной осью (безрисковая ставка) часто обозначают как награда за ожидание. Наклон CML называют наградой за единицу принятого риска. Таким образом, эти две величины можно интерпретировать как цены времени и риска.
Очевидно, что если линия безразличия какого-то инвестора касается CML в точке М, то он и выберет портфель М. Если уровень риска, характеризующийся величиной σm, его не устраивает, он может инвестировать часть своих средств в покупку безрисковых активов, имеющих норму отдачи rf. Как правило, безрисковыми ценными бумагами являются краткосрочные государственные обязательства. Покупка этих активов представляет собой предоставление денег государству в долг.
Портфель этого инвестора будет располагаться на участке rfM линии CML. Этот участок характеризует портфели всех инвесторов, дающих деньги в долг. Участок линии MG характеризует портфели инвесторов, склонных к повышенному риску.
Для осуществления рискованных инвестиций (сRp > Rm) они занимают деньги по пониженной ставке (Rp < Rm). Таким образом, участок MG линии CML характеризует портфели инвесторов, занимающих деньги.
Поскольку эффективный портфель состоит из N ценных бумаг, уравнение (5.1) справедливо для любой ценной бумаги, имеющейся на рынке. Это дает возможность построить рыночную линию ценной бумаги SML (security market line) рис. 36.
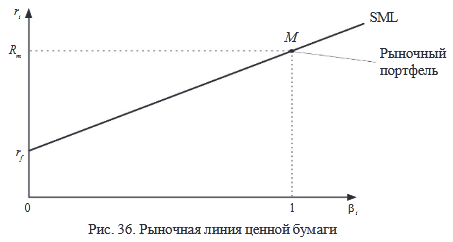
β – коэффициент – коэффициент наклона линии SML.
Акция, которая имеет доходность, являющуюся зеркальным отражением доходности рыночного портфеля М, имеет β = 1. Такие акции называются нейтральными (рис. 37).
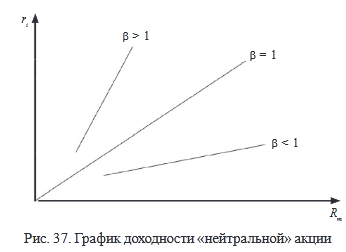
Акции со значением β > 1 называются агрессивными. Они повышаются в цене быстрее, чем рыночная цена в целом (но и падают быстрее).
Акции со значением β < 1 называются защищающимися. Их флуктуация меньше, чем флуктуация рыночной цены в целом.
Численные значения некоторых показателей, входящих в CAPM, на финансовом рынке США (по данным американских источников):
а) за период с 1926 по 1987 г. Rm = 12 %;
б) премия за риск относительно долгосрочных правительственных облигаций:
Rm – rf = 6,8 %.
Премия за риск относительно казначейских билетов:
Rm – rf = 8,3 %;
в) безрисковая ставка процента: rf = 7 %.
Трудности, связанные с использованием CAPM в условиях реального рынка:
а) практически очень трудно найти для всех портфелей необходимые средние значения Rp, дисперсии σ2 и ковариации; б) возможность брать неограниченные займы по безрисковой ставке представляется сомнительной, поэтому модель подверглась усовершенствованию в работах Блэка, Дженсена и Сколса; в) в реальных условиях необходимо учитывать налоги; г) значения ri меняются во времени; д) нельзя не учитывать стоимость заключения сделки и стоимость информации.
Разность (Rm – rf) × βi характеризует премию за систематический риск, т. е. риск, возникающий в результате колебаний доходности на всем рынке ценных бумаг.
В модели САРМ нет корректировки на риск несистематический, так как предполагается, что диверсифицированный риск стремится к нулю при очень большом количестве различных видов инвестиций.
Рыночный и собственный риск
Общий риск ценной бумаги i состоит из двух частей:
1) рыночный (систематический) риск (market risk) – σS;
2) собственный (несистематический) риск (unique risk) – σNS.
Диверсификация портфеля приводит к усреднению рыночного риска, но не снижает его (рис. 38).
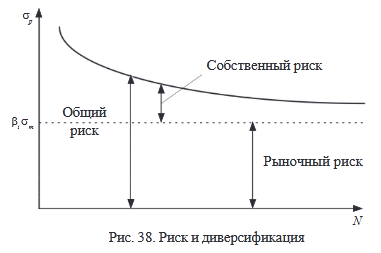
Собственный риск снижается при диверсификации портфеля. Как следствие, снижается общий риск портфеля.
Цифровые методы оценки эффективности инвестиций
Принимая решение об инвестировании средств в тот или иной проект, необходимо оценить его экономическую эффективность. Для этого разработаны средства автоматизации – программы инвестиционного анализа, моделирующие развитие проекта. При выборе таких программ следует четко представлять себе их возможности и особенности.
На российском рынке наиболее распространены несколько программ (табл. 19), в основе которых лежат классические подходы к оценке инвестиций. Разработчики этих пакетов регулярно выпускают новые, более гибкие версии, ежегодно увеличивая число пользователей. Существуют также менее известные программные пакеты, созданные на основе электронных таблиц и разработанные, как правило, консалтинговыми фирмами.
Т а б л и ц а 19
| Программа | Разработчик | Стоимость, долл. |
|---|---|---|
| COMFAR | UNIDO | 500–5 200 |
| Project Expert | ПО «ПРО-Инвест» | 470–10 500 |
| Альт-Инвест | ИКФ «Альт» | 475–1 000 |
| ТЕО-Инвест | Институт управления проблем РАН | 980–1 100 |
| Energy Invest | Научный центр прикладных исследований | 400 |
| Инвестор PL/Millenium III | Общество финансового и экономического развития РОФЭР | 200 |
| Инек-Холдинг | ИНЭК | 2 650 |
Во всех программных продуктах для анализа инвестиционных проектов методика и общие подходы к расчетам примерно одинаковы. Поэтому правильнее рассматривать такие пакеты, как некие инструменты, каждый из которых применим в конкретной ситуации. Сегодня функциональные возможности последних версий пакетов для расчетов инвестиционных проектов находятся примерно на одном уровне.
На настоящий момент все программные продукты позволяют:
- разработать детальный финансовый план и оценить потребность в денежных средствах в будущем;
- определить схему финансирования инвестиционного проекта;
- оценить возможность и эффективность привлечения денежных средств из различных источников финансирования;
- разработать план производства и развития предприятия;
- определить эффективную стратегию маркетинга и рационального использования материальных, трудовых и финансовых ресурсов;
- рассчитать и проанализировать различные сценарии развития проекта, варьируя значения факторов, способных повлиять на финансовые результаты;
- контролировать процесс реализации инвестиционного проекта.
При выборе конкретного программного продукта для расчета эффективности инвестиций прежде всего нужно определить уникальность и отраслевые особенности конкретного проекта.
Программы для автоматизации расчетов инвестиционных проектов условно можно разделить на две группы. Первая – универсальные пакеты, не зависящие от отрасли и конкретной задачи (например, COMFAR, Project Expert, «Альт-Инвест», «ИНЭК-Холдинг», «ТЭО-Инвест»); вторая – отраслевые (например, Energy Invest).
Для отдельных инвестиционных проектов, которые трудно просчитать не только с помощью универсальной программы, но и с помощью отраслевой, разрабатываются индивидуальные модули. Такими разработками, в частности, занимается фирма «Интеринвестпроект».
Наиболее приемлемыми программными продуктами по оценке эффективности инвестиционных проектов являются отраслевые программы. В них учитываются особенности исходной информации (нормативной, правовой, экономической, методической и пр.), используется база данных по отечественным и зарубежным инвестиционным проектам в конкретной отрасли. В большинстве случаев отраслевые программы дешевле универсальных.
Недостатком универсальных пакетов является необходимость выполнения большого количества вспомогательных расчетов. Кроме того, применяя эти программы, сложнее сопоставить исходную информацию в первичной документации с показателями, используемыми такой программой. Однако если расчет инвестиционного проекта производят профессионалы, располагающие обширными базами данных по отрасли и знающие ее специфику, то использование универсальных пакетов может быть предпочтительнее отраслевых. Например, «Альт-Инвест» хорошо зарекомендовал себя в машиностроительной промышленности, «ИНЭКХолдинг» – при проведении санации предприятий, а Project Expert – в энергетической и металлургической отраслях.
Многие предприятия успешно используют индивидуальные пакеты, разработанные на базе электронных таблиц под конкретный инвестиционный проект.
Таким образом, при выборе программы надо учитывать субъективные факторы, которые важны для каждого конкретного предприятия.
Порядок работы со всеми программами примерно одинаков. Сначала вводится исходный набор параметров, характеризующих проект: информация о производственной программе, маркетинговый план, схема финансирования проекта и т. д. Результаты всегда отражаются в трех главных финансовых отчетах: отчете о прибылях и убытках, бухгалтерском балансе и отчете о движении денежных средств.
Затем аналитик, работающий с программой, оценивает результаты и вводит исходные данные для новых расчетов. Например, есть два варианта получения оборудования: приобретение его на кредитные средства или использование лизинговой схемы. Каждый из этих вариантов с помощью программы рассчитывается отдельно, после чего выбирается наиболее эффективный.
При использовании программ, автоматизирующих расчет инвестиционного проекта, важно не угодить в «ловушку простоты». Ее суть в том, что фундаментальность заложенных в программы методик расчета создает иллюзию высокой надежности полученных результатов. Но не все так просто.
Методики действительно надежные и проверенные. Но в основе всех расчетов лежат исходные данные, от правильности которых зависит конечный результат. Критичной является информация о планируемом объеме продаж. Всегда существует вероятность, что реальные объемы продаж будут отличаться от планируемых. Возможные изменения нужно предвидеть и тщательно контролировать, так как их появление не может служить оправданием плохих результатов инвестиционного проекта. Поэтому принципиально важно уже на стадии разработки проекта провести анализ устойчивости: как изменятся параметры эффективности проекта при варьировании цен, объемов сбыта и других исходных данных.
Поскольку программные продукты для оценки инвестиционных проектов обладают примерно одинаковыми возможностями, успешность их применения во многом зависит от квалификации работающего с ними персонала. Под квалификацией имеется в виду не только грамотная работа с программой, но и умение правильно определить исходные данные для расчета.
