К.э.н., доцент Степанова Т.А., асс. Закупнев С.Л., студентка Кот А.О.
Воронежский государственный аграрный университет имени императора Петра I, Россия
Прогнозирование урожайности подсолнечника и финансового результата на основе статистическо-аналитического выравнивания ряда динамики
В данной статье на примере ЗАО “Путь Ленина” Аннинского района Воронежской области мы составим прогноз урожайности подсолнечника до 2017 года включительно. Прогнозные значения мы получим, используя метод выявления тенденции в изменении урожайности - аналитическое выравнивание. Этот метод позволяет выявить ту функцию, которая наиболее правильно описывает фактическую динамику урожайности. Следовательно, уравнение этой функции можно использовать для составления прогнозов на будущий период. Прогнозирование начнём относительно фактической урожайности, зафиксированной с 2006 года по 2014 год. В таблице 1 представим характеристику полученных уравнений выравнивания.
Таблица 1 – Характеристика полученных уравнений выравнивания фактической урожайности подсолнечника
|
Названия функции |
Уравнения выравнивания (общий вид) |
Уравнения выравнивания |
R2 |
|
Линейная |
|
0,8348t+28,065 |
0,1321 |
|
Экспоненциальная |
|
0,082 |
|
|
Логарифмическая |
|
2,5322ln(t)+28,637 |
0,0839 |
|
Полиномиальная |
|
0,2267t2-1,4326t+32,222 |
0,1822 |
|
Степенная |
|
28,702t0,0668 |
0,043 |
Статистическая характеристика уравнений выравнивая, представленных в данной таблице позволяет нам сделать вывод, что благодаря полиномиальной функции мы сможем наиболее точно определить прогнозные значения на 2015, 2016 и 2017 года. Величина достоверности аппроксимации (R2) полиномиальной функции имеет большее значение среди всех функций, следовательно, полиномиальная функция наиболее приближена к исходной. Однако для проверки необходимо дать интерпретацию теоретической и прогнозной урожайности подсолнечника. Результаты представим в таблице 2.
Таблица 2 – Фактическая и прогнозная урожайность подсолнечника
|
Годы |
Фактическая урожайность, ц/га |
Выровненные значения по уравнениям |
||||
|
Линейная функция |
Экспонен-циальная функция |
Логариф-мическая функция |
Полиномиаль-ная функция |
Степенная функция |
||
|
2006 |
29,99 |
28,9 |
28,65 |
28,64 |
31,02 |
28,7 |
|
2007 |
31,15 |
29,73 |
29,35 |
30,39 |
30,26 |
30,06 |
|
2008 |
32,23 |
30,57 |
30,07 |
31,42 |
29,96 |
30,89 |
|
2009 |
34,65 |
31,40 |
30,8 |
32,15 |
30,12 |
31,49 |
|
2010 |
17,92 |
32,2 |
31,56 |
32,71 |
30,73 |
31,96 |
|
2011 |
33,11 |
33,07 |
32,33 |
33,17 |
31,79 |
32,35 |
|
2012 |
37 |
33,91 |
33,12 |
33,56 |
33,3 |
32,69 |
|
2013 |
40,9 |
34,74 |
33,93 |
33,9 |
35,27 |
32,98 |
|
2014 |
33,2 |
35,58 |
34,77 |
34,2 |
37,69 |
33,24 |
|
Прогнозные значения |
||||||
|
2015 |
36,41 |
35,62 |
34,47 |
40,57 |
33,47 |
|
|
2016 |
37,25 |
36,49 |
34,71 |
43,89 |
33,69 |
|
|
2017 |
38,08 |
37,38 |
34,93 |
47,68 |
33,88 |
|
Для того чтобы прогнозные значения на будущий период для ЗАО ”Путь Ленина” были наиболее точными выполним ещё одно аналитическое выравнивание по скользящей средней урожайности. Так как, в том случае, если временной ряд содержит даже незначительную ошибку, то выявление тренда правильнее будет проводить путем сглаживания. Это метод, который включает в себя некоторый способ локального усреднения данных, а в результате несистематические компоненты взаимно погашают друг друга. Именно скользящее среднее является основным методом сглаживания. Главным преимущество данного вида сглаживания состоит в том, что результаты становятся более устойчивыми и достоверными, в том случае если в статистических данных была допущена ошибка. Выполним аналитическое выравнивание и характеристику полученных уравнений запишем в таблицу 3.
Таблица 3 – Характеристика полученных уравнений выравнивания урожайности подсолнечника по скользящей средней
|
Название функции |
Уравнения выравнивания (общий вид) |
Уравнения выравнивания |
R2 |
|
Линейная |
|
0,98t+28,02 |
0,3188 |
|
Экспоненциальная |
|
28,352e0,0288t |
0,2937 |
|
Логарифмическая |
|
2,1573ln(t)+29,373 |
0,1552 |
|
Полиномиальная |
|
0,639t2-4,1324t+35,749 |
0,7254 |
|
Степенная |
|
29,507t0,0619 |
0,1361 |
Величина достоверности аппроксимации (R2) полиномиальной функции, так же как и при аналитическом выравнивании по фактической урожайности, выше, чем у других функций. Для выявления прогнозных значений урожайности произведем расчеты по скользящей средней урожайности, результаты запишем в таблицу 4.
Таблица 4 – Скользящая средняя и прогнозная урожайность подсолнечника
|
Годы |
Скользящая средняя урожайность, ц/га |
Выровненные значения по уравнениям |
||||
|
Линейная функция |
Экспонен-циальная функция |
Логариф-мическая функция |
Полиномиаль-ная функция |
Степенная функция |
||
|
2006 |
29,0 |
29,18 |
29,37 |
32,26 |
29,51 |
|
Продолжение таблицы 4
|
2007 |
31,12 |
29,98 |
30,03 |
30,87 |
30,04 |
30,8 |
|
2008 |
32,68 |
30,96 |
30,91 |
31,74 |
29,1 |
31,58 |
|
2009 |
28,27 |
31,94 |
31,81 |
32,36 |
29,44 |
32,15 |
|
2010 |
28,56 |
32,9 |
32,74 |
32,84 |
31,06 |
32,59 |
|
2011 |
29,34 |
33,9 |
33,69 |
33,24 |
33,96 |
32,97 |
|
2012 |
37,00 |
34,88 |
34,68 |
33,57 |
38,13 |
33,28 |
|
2013 |
37,03 |
35,86 |
35,69 |
33,86 |
43,59 |
33,56 |
|
2014 |
36,84 |
36,74 |
34,11 |
50,32 |
33,81 |
|
|
Прогнозные значения |
||||||
|
2015 |
37,82 |
37,81 |
34,34 |
58,33 |
34,03 |
|
|
2016 |
38,8 |
38,92 |
34,55 |
67,61 |
34,23 |
|
|
2017 |
39,78 |
40,06 |
34,73 |
78,18 |
34,41 |
|
Сравнив показатели, можно сделать вывод о том, что полиномиальная функция в обоих случаях должна определить наиболее точные прогнозные значения урожайности подсолнечника, так как величина достоверности аппроксимации (R2) этой функции выше, чем у других. Анализ показателей, рассчитанных по фактической и скользящей средней урожайности, показывает, что расхождения всё же присутствуют. Однако прогнозные показатели, рассчитанные благодаря полиномиальной функции, очень высоки и не могут отражать действительную урожайность.
Несмотря на значение R2, исходя из значения среднего абсолютного прироста (0,3ц/га), за 3 года урожайность увеличится на 1 ц/га. Следовательно, прогнозное значение по скользящей средней урожайности подсолнечника составит приблизительно 38,03 ц/га в 2016 году и 38,33 ц/га в 2017 году. Тогда можем сделать вывод, что реальный прогноз мы можем построить по линейной функции, хотя и с наиболее высокой ошибкой.
Для анализа используем показатель площади посева подсолнечника в ЗАО “Путь Ленина” за 2014 год, который составил 800 га (валовой сбор в этом году составил 26560 ц), и данные таблицы 4. Таким образом, в 2015 году мы получим 30256 ц подсолнечника, в 2016 году 31040 ц подсолнечника, а в 2017 году 31824 ц.
Средняя цена семян подсолнечника в России в 2015 году составила 2010 руб. за 1 центнер. Исходя из данной цены, мы получим дополнительно 7 млн. 428 тыс. 960 руб. ((20256-26560)ц ×2010руб.) в 2015 году, 1 млн.575 тыс. 840 руб. ((31040-30256)×2010руб.) в 2016 году и 1 млн. 575 тыс. 840 руб.
((31824-31040)ц×2010 руб.) в 2017 году.
Таким образом, наблюдается значительный прирост выручки за реализацию подсолнечника в 2015,2016 и 2017 годах. В 2013 году Воронежская область вошла в ТОП-10 регионов с наибольшими посевными площадями подсолнечника, валовой сбор был высок, что позволило увечить экспортные поставки подсолнечника российского производства.
Cписок использованной литературы:
1. Ануфриева А.В. Анализ развития малых форм хозяйствования на селе Воронежской области и их роль в производстве продукции животноводства/ А.В. Ануфриева, И.М. Сурков // Вестник государственного аграрного университета. -2015- №4(47).- С.280-287
2. Ануфриева А.В. Оценка развития зернового рынка в Российской Федерации. /А.В. Ануфриева, Е.Б. Панина, О.А. Письяукова // Журнал научных публикаций аспирантов и докторантов.№12(102). - Курск,2014- С.60-63
3. Коротеев В.П. Резервы снижения себестоимости продукции растениеводства на примере ПСК ”Правда” Терновского района Воронежской области / Ю.А. Дынина, В.П. Коротеев // Молодежный вектор развития аграрной науки: материалы 63-й научной студенческой конференции. – Воронеж,2012. – Ч.2 – С.51-53
4. Панина Е.Б. Перспективы и стратегия развития Павловского района Воронежской области в сфере сельского хозяйства / Е.Б. Панина, Е.И. Якушова, А.И. Панин // Актуальные проблемы социально-экономического развития экономических систем: Материалы V Всероссийской научно - практической конференции. – 2015.-С.188-197
5. Улезько А.В. Управление производством масличных культур на основе кластерного подхода/ Т.В. Савченко, А.В. Улезько, Н.Н. Кравченко. – Воронеж: ВГАУ,2013. – 160с.

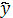 1=a0t+a1
1=a0t+a1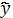 1=a0ea1
1=a0ea1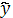 1=a0ln(t)+a1
1=a0ln(t)+a1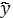 1=a0t2-a1t+a2
1=a0t2-a1t+a2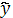 1=a0ta1
1=a0ta1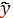 1=a0t+a1
1=a0t+a1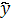 1=a0ea1
1=a0ea1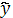 1=a0ln(t)+a1
1=a0ln(t)+a1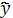 1=a0t2-a1t+a2
1=a0t2-a1t+a2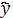 1=a0ta1
1=a0ta1