К.э.н. Ивинская Е.Ю., студент гр.9104 Храмова К.А., студент гр.9104 Милютина Ю.Ю.

Казанский научно-исследовательский технический университет им.А.Н.Туполева

Применение математики гармонии в экономических процессах

Любое предприятие в рамках жизненного цикла неизбежно сталкивается с кризисом развития, что обусловлено возникающими диспропорциями, т.е. отсутствием гармонии между видами внутренних процессов функционирования и развития и внешних воздействий. Одним из современных направлений в управлении предприятием, регионом, государством становится гармоничный менеджмент, возникший на рубеже XX-XXI вв. Это стало возможным благодаря развитию теории гармонии и выделению А.П. Стаховым в математической науке отдельного направления – математики гармонии [1]. Исследования в экономике на наличие в ней признаков гармонии свидетельствуют о соразмерности в пропорциях бизнес-процессов, что существенно усиливает адаптационные свойства предприятия, обеспечивают его стабильное эффективное функционирование и устойчивое развитие благодаря структурной трансформации на новом качественном уровне.

Гармоничных соотношений должно существовать неограниченное множество, доминирующие свойства систем в линейном, плоскостном и объемном пространстве должны характеризоваться различными гармоничными пропорциями, ключевыми для конкретной системы, а не только золотой пропорцией. В свою очередь целое может содержать различное количество составных частей, что ведет к необходимости использовать в методах гармонизации вурфные соотношения, причем многозвенных вурфов. Гармоничный подход находит свое место в когнитивном управлении инновационной экономикой, характеризующейся высокой интенсивностью использования больших объемов знаний в производственно-технологических процессах и системах управления. Гармоничный подход должен занять место и в экономико-эколого-социальной системе.

Гармония как объективная реальность существует и должна проявлять себя в различных системах, включая экономику, гармонизацию определяют как своеобразный процесс стремления любой сложной системы к гармоничным пропорциям частей и целого. Сложные системы, к которым относятся промышленные предприятия, состоят из иерархических структур (уровней). В наиболее прогрессивных из них предпочитают пользоваться правилом деления целого на доли между операторами (стейкхолдерами, конкурентами) в золотоносных показателях.

Обычно части соотносят в золотой пропорции или золотом сечении, выражая величиной 0,618 и 0,382, или 61,8% и 38,2%. Впрочем, могут и должны быть и другие значения сообразно иным гармоничным пропорциям. Композиция целого из трех частей, например, проявляется в следующих долевых видах:

1) производственные издержки, собственные доходы и отчисления в общественный бюджет в пропорции 0,618 + 0,618 + 0,382 = 1,618;

2) собственные, долгосрочные и краткосрочные заемные средства.

Золотая пропорция сопровождает любой большой объем выборок случайных величин с нормальным законом распределения [2]. Тем не менее системы с параметрами, описываемыми гауссовыми распределениями как нормальной, так и иной формы с конечными моментами первого и второго порядков, имеют тенденцию к самоорганизации с характерным принципом. Его смысл в том, что рост сложности гауссовой экономической системы, состоящей из множества гауссовых подсистем, самопроизвольно влечет процесс самоорганизации этой структуры, т.е. порождает стремление к соотношению между шенноновскими мерами хаоса и порядка, близкому к золотой пропорции. Нормальный закон распределения традиционно характеризуется принципом двойственности: его координатные свойства описываются экспонентой, а структурные – степенной функцией. Сказанное непосредственно следует из формулы Гаусса (гауссианы), полученной из биномиального распределения при некоторых допущениях. График функции имеет колоколообразную форму и определяется формулой

где А – размах функции;

t – время; -∞< t <∞;

а – параметр функции, характеризующий ее длительность на уровне 0,606А.

В этой математической модели показана цикличность (в данном случае экономического процесса). Это следует из возможности формирования колоколообразной функции путем суммирования гармонических колебаний синусоидальной и косинусоидальной зависимости, преобразованных определенным образом [3]. Получаемый результат своеобразно иллюстрирует формулу Эйлера 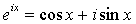, где i – мнимая единица. Колоколообразная кривая также может быть получена путем перемножения двух этих функций [4]. Отсюда смеем утверждать, что экспоненте, а, следовательно, и нормальному закону распределения свойственна цикличность с периодом, характеризующим длительность цикла. Изложенное вносит дополнительное объяснение наличия у рыночной экономики циклов различной периодичности, делая ее повторяющейся, циклической, кризисной. Следовательно, при моделировании экономических систем необходимо учитывать тройственное проявление нормального закона распределения случайной величины, включая цикличность.

Считается, что гармоничный рынок – это эталонная система товарообмена, в которой между ее ключевыми компонентами и процессами прослеживается принцип золотого сечения, обеспечивающий сложной социально-экономической системе (в данном случае рынку) максимум скорости увеличения энтропии, т. е. максимальное наращивание разнообразия товаров, и минимум затрат на обеспечение собственной системной устойчивости. Следовательно, интересы благоприятной эволюции экономики должны диктовать политику формирования гармоничных рыночных цен, которые в свою очередь диктуют экономическую политику, но не наоборот.

Литература:

1. Стахов А.П. Математизация гармонии и гармонизация математики // Академия Тринитаризма. М., эл. № 77-6567, публ.16897. М., 2011.

2. Иванус А.И. Золотое сечение в системах с биномиальным законом распределения // Академия Тринитаризма. М., эл. № 77-6567, публ. 13681.

3. Шенягин В.П., Цветков В.А., Краснов Е.М., Деренкин В.П. Формирователь колоколообразных импульсов / Авторское свид-во СССР № 849479, МКИ H О3 K 6/06, описание изобретения. Заявл. 26.06.79, опубл. 23.07.81, бюл. № 27.

4. Шенягин В.П., Нефедов В.И., Битюков В.К. Методы формирования колоколообразных импульсов / 4-я Международная научно-техническая конференция «Космонавтика. Радиоэлектроника. Геоинформатика». Рязань: Рязан. гос. радиотехн. акад., 2003.