Пятибратов А.К., Трач А.А.

Одесский национальный политехнический университет

Оптимальная диверсификация портфеля ценных бумаг

1. Классическая модель Марковица.

Классическая задача портфельной оптимизации, впервые рассмотренная Г. Марковицем, базируется на допущениях о нормальности распределения доходностей акций и стационарности финансовых процессов. Математическая модель формирования оптимального портфеля Марковица состоит в следующем [1]. Для 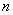рисковых ценных бумаг при известных ожидаемых эффективностях 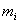и ковариациях 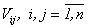этих ценных бумаг, требуется выбрать такие доли 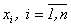в портфеле 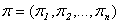инвестора, которые минимизировали бы риск портфеля при заданном уровне его ожидаемой эффективности 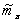. Аналогично формулируется обратная задача: для 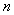рисковых ценных бумаг при известных ожидаемых эффективностях 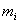и ковариациях 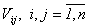этих ценных бумаг, требуется выбрать такие доли 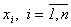в портфеле 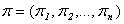инвестора, которые максимизировали доходность портфеля при заданном уровне риска 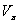. В предположении, что ковариационная матрица 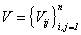определена и существует обратная матрица, оптимизация в обоим случаях сводится к решению задачи выпуклого квадратичного программирования.

Позже работа Марковица была дополнена исследованиями Д. Тобина [2]. Д.Тобин обнаружил, что решение задачи выбора оптимального портфеля инвестора упрощается и приобретает некоторые особенности, если учитывать наличие на рынке безрисковых ценных бумаг. С практической точки зрения, гипотеза Тобина о наличии абсолютно безрисковых активов на рынке некорректна, и реально рассматриваются слаборисковые активы, например, государственные облигации с фиксированным доходом или казначейские векселя. То есть, речь идет о пренебрежении слабым риском. С этого момента в теории и на практике основной задачей становится не просто нахождение оптимального портфеля ценных бумаг, но и правильное распределение капитала между рисковыми и безрисковыми активами. В связи с этим, постановка задачи несколько меняется. Кроме рисковых, в портфель ценных бумаг включается также безрисковая бумага, с соответствующей долей 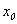и ожидаемой доходностью 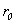. Тогда ожидаемая эффективность портфеля:

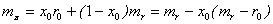, (1)

где 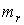- ожидаемая эффективность рисковой части портфеля.

Очевидно, что 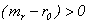, так как в противном случае нет смысла для инвестора идти на риск. По тем же соображениям ожидаемая эффективность каждой из рассматриваемых ценных бумаг 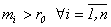, иначе инвестор просто заменил бы активы, не удовлетворяющие этому условию, на безрисковые, увеличивая при этом ожидаемую эффективность портфеля и вместе с тем сокращая риск. Дисперсия же всего портфеля определяется только рисковой его частью:

, (2)

Задача Тобина выбора оптимального портфеля аналогична первому варианту задачи Марковица.

Модель Марковица рационально использовать при стабильном состоянии фондового рынка, когда желательно сформировать портфель из ценных бумаг разного характера, которые принадлежат разным областям. Основной недостаток модели - ожидаемая доходность ценных бумаг принимается равной средней доходности по данным прошлых периодов. Кроме того, на практике зачастую не выполняются базовые допущения модели.

2. Факторные модели.

Модель Шарпа. Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом [2]. Эту взаимосвязь отражают функцией линейной регрессии вида:

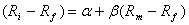, (3) где 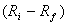, 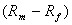- соответственно, отклонение доходности ценной бумаги и доходности рынка от безрисковой ставки; 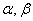- коэффициенты регрессии.

Модель Шарпа является однофакторной моделью, в качестве фактора выступает доходность рыночного индекса. Эта модель широко используются при формировании портфеля ценных бумаг многими практикующими инвесторами.

Основной недостаток модели Шарпа - необходимость прогнозировать доходность фондового рынка и безрисковую ставку доходности. Модель не учитывает риск колебаний безрисковой доходности. Кроме того, при значительном изменении соотношения между безрисковой доходностью и доходностью фондового рынка модель дает погрешности. Модель Шарпа может применяться при рассмотрении большого количества ценных бумаг, которые описывают большую часть относительно стабильного фондового рынка.

Модель САРМ. При выборе портфеля ценных бумаг систематический риск можно подавить путем подбора активов, не коррелированных с глобальным рынком, то есть включать в портфель активы со значениями 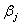, близкими к нулю. При построении регрессии (1) коэффициент 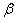вычисляется по формуле:

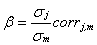, (4)

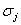- стандартное отклонение доходности 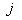-го актива,

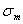- стандартное отклонение доходности по рынку в целом,

- коэффициент корреляции доходности 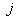-го актива и рынка.

Таким образом, 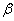показывает направление движения цены актива относительно направления движения рынка в целом. Идеальной является бумага, для которой 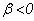, то есть, рынок и цена актива движутся разнонаправлено. Но на практике такая ситуация возникает очень редко. Поэтому предпочтение отдают тем бумагам, для которых 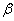имеет значение, близкое к нулю.

Арбитражная теория расчетов (АРТ). В теории АРТ, называемой иногда также «теорией риска и возврата», глобальные факторы описываются не одной относительной доходностью, а несколькими факторами, представленными случайными величинами 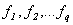, это могут быть цены на нефть, на металл, объем урожая зерновых и пр. Модель разработана С. Россом [4] и применима также как и модель Шарпа в условиях равновесия рынка.

Пусть на рынке торгуются 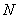активов 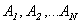. Для каждого 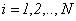случайная относительная доходность актива 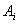представляется в виде линейной комбинации

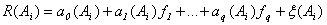, (5)

где шумовая составляющая 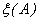некоррелирована с глобальными факторами.

Для большинства активов 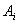при больших 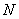справедливо приближенное равенство для процентной ставки

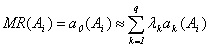(6)

Таким образом, случайное значение процентной ставки, при больших значениях 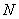, есть линейная комбинация коэффициентов зависимости от глобальных факторов. Чтобы воспользоваться этой моделью, нужно рассчитать столько линейных моделей, сколько выбрано активов. Поскольку предполагается, что число активов велико, то вычислительная процедура становится весьма трудоемкой. Кроме того, ситуация на рынке быстро меняется, и такого типа модели не могут использоваться на длительном временном горизонте. Для того, чтобы модель адекватно соответствовала ситуации, ее нужно строить заново. В таком случае возникает проблема ее адекватности и проблема проверки качества становится неразрешимой.

Данная модель относится к многофакторным моделям. Она учитывает основные экономические воздействия, влияние которых отражается на стоимости ценных бумаг. К группе многофакторных моделей относится и модель BARRA [3], разработанная в 1970г. Розенбергом, которая кроме рыночных показателей, учитывает финансовые показатели (в частности данные баланса) компаний. В модели используется 68 различных фундаментальных и промышленных факторов.

3. Нечетко-множественный подход.

Альтернативой классической модели Марковитца стал нечетко-множественный поход в оптимизации инвестиционного портфеля, предложенный в работе [5] и развитый в [6]. Основные принципы и идея метода:

1. Риск портфеля — это возможность того, что ожидаемая доходность портфеля окажется ниже некоторой предустановленной плановой величины.

2. Корреляция активов в портфеле не рассматривается и не учитывается.

3. Доходность каждого актива — это неслучайное нечеткое число (например, треугольного вида или интервального вида). Аналогично, ограничение на предельно низкий уровень доходности может быть как обычным скалярным, так и нечетким числом произвольного вида. Таким образом, два источника информации (средняя доходность и волатильность актива) сводятся в один (расчетный коридор доходности или цены) и тем самым объединяются два источника неопределенности в один.

4. Оптимизировать портфель в такой постановке означает максимизировать ожидаемую доходность портфеля в точке времени T при фиксированном уровне риска портфеля (по аналогии с тем, как это делается в [1] и [2]).

Рассмотренные методы относятся к числу наиболее значимых и заметных результатов, на основании которых строятся другие – новые, сложные и точные, однако и более трудоемкие. Все они в совокупности образуют сложную математическую теорию. Усложнения касаются различных параметров и предположений относительно модели. Грамотно диверсифицированный на базе конкретного фондового индекса портфель на развитом рынке имеет риск, близкий к рыночному. При этом его доходность близка к доходности выбранного рыночного индекса, под который и

осуществлялась диверсификация. Как показали практика и анализ, 70-80% несистематических рисков устраняются в портфеле, включающем (7-10) акций, а 90% - в портфеле, состоящем из (12 - 18) акций. Существуют методики расчета классических моделей в Microsoft Excel. Например, в [7] приведена методика расчета портфеля Марковица, а в [8] – портфеля Тобина.

В заключение отметим, что при распределении инвестиций по активам, следует учитывать, что активы должны иметь слабую корреляцию друг с другом для того, чтобы убытки по одному активу могли компенсироваться прибылями по другому.

Литература

1. Боди З., Кейн А., Маркус А. Принципы инвестиций. -М.: Издательский дом “Вильямс”, 2008. - 984 с.

2. Tobin J. The Theory of Portfolio Selection/J. Tobin// Theory of Interest Rates/ Ed. by F.H. Hahn, F.P.R.Brechling.-London: MacMillan, 1965.-Pp.3-51/

3. Шарп У., Александер Г., Бэйли Дж. Инвестиции: пер. с англ. - М.: ИНФРА-М, 2003. , 1028 с.

4. Ross S.A. The Arbitrage Theory of Capital Assert Pricing/ S.A. Ross// Journal of Economy Theory. -1976.- Vol.13. №3.-Pp.343-362.

5. Шведов А.С. Теория эффективных портфелей ценных бумаг.- М.: Финансы «ГУ ВШЭ», 1999.- 140с.

6. Зайченко Ю. П., Малихех Есфандиярфард. Анализ модели оптимизации нечеткого портфеля//Веснік НТУУ«КП» Інформатика, управління та обчислювальна техника -№50.-2009.-С.198-204.

7. Андриенко В. М.,Голованова Е.Ю. Оптимизация портфеля инвестиций в Microsoft Excel. Materialy v miedzynarodjwej naukowi-praktycznej konferencji «Perspektywiczne opracowania sa nauka I technikami-2009».- Przemysl.- Nauka i studia.-2009.-С.27-34.

8. Жданов И.Ю. Инвестиционный портфель Тобина. Принципы построения/ Электронный ресурс. – Режим доступа: http://finzz.ru/investicionnyj-portfel-cennyx-bumag-portfel-tobina-v-excel.html. Загл. с экрана.