Волкова А.А., магистрант группы УА-21НП

Карагандинский экономический университет Казпотребсоюза, Казахстан

Анализ управленческих решений периода

Ключевые слова: анализ, затраты.

Любое предприятие функционирует в условиях того или иного лими­тирующего фактора. А иногда таких факторов может быть несколь­ко.

В тех случаях, когда решение затрагивает только один лимитирующий фактор, для максимального увеличения прибыли следует применить следующую процедуру:

определить маржинальный доход на единицу лимитирующего фактора для каждой единицы продукции или услуг. Например, если лимити­рующим фактором являются трудозатраты, тог­да нужно разделить удельный маржинальный доход для каждой из единиц продукции на ко­личество часов, необходимых для производства каждой единицы продукции; в результате этого действия получится маржинальный доход в расчете на единицу лимитирующего фактора;

вынести управленческое решение, основываясь на суммарных ресурсах лимитирующего факто­ра, при этом производить продукцию в порядке уменьшения размера маржинального дохода на единицу лимитирующего фактора. То есть если при производстве максимального количества изделий с наивысшим показателем маржиналь­ного дохода, которые могут быть реализованы предприятием, используется только половина общего ресурса лимитирующего фактора, тогда оставшаяся часть ресурсов должна быть исполь­зована для выпуска других изделий в порядке уменьшения их показателя маржинального до­хода на единицу лимитирующего фактора. При помощи описанной выше процедуры зада­ча максимального увеличения прибыли достигает­ся через максимизацию маржинального дохода, получаемого компанией.

Рассмотрим пример,

Компания производит следующие три вида про­дукции. В настоящий момент максимально возмож­ное время работы оборудования составляет 20 000 машино-часов. Ниже приводится информация о прогнозируемом спросе и требуемых производ­ственных мощностях:

В настоящее время мощность оборудования ог­раничена 20 000 часами работы, но этого недостаточно, чтобы удовлетворить общий, спрос на про­дукцию. Необходимое время работы для удовлет­ворения общего спроса составляет:

15 000 + 9000 + 6 000 = 30 000 часов работы оборудования.

Таким образом, лимитирующим фактором в этом случае служит количество часов работы оборудо­вания.

Для решения подобной проблемы необходимо определить маржинальный доход в расчете на еди­ницу лимитирующего фактора и провести соответ­ствующее ранжирование:

Таким образом, компания должна использовать имеющийся ресурс времени работы оборудования, в первую очередь для производства продукта 3, при этом затраченное время для его производства составит:

3 000 единиц * 2 машино-часа на единицу = 6 000 машино-часов.

Затем компания будет производить продукт 2, при этом затраченное для его производства время составит:

3 000 единиц *З машино-часа на единицу = 9 000 машино-часов.

Так как по лимитирующему фактору остался ресурс 5 000 машино-часов (20 000машино-часов - (6 000 машино-часов + 9 000 машино-часов)), то компания имеет возможность произвести продукт 1 в количестве 1 000 единиц (5 000 / 5).

При такой производственной программе компа­ния заработает маржинальный доход в размере:

15 долл. США * 3 000 единиц (продукт 3) +

18 долл. США * 3 000 единиц (продукт 2) +

25 долл. США * 1 000 единиц (продукт 1) = 124 000 долл. США.

Если бы компания определяла оптимальную структуру производственной программы по маржи­нальной прибыли из расчета на единицу продук­ции, а не по ограниченному фактору, то в первую очередь она бы производила продукт 1. Затрачен­ное время для производства составило бы:

3 000 единиц * 5 машино-часов на единицу = 15 000 часов.

На остаток лимитирующего фактора:

20000 часов - 15 000 часов = 5 000 часов

производила продукт 2 в количестве: 1 667 единиц (5 000 часов / 3). При этом компания заработала бы маржинальный доход в сумме:

25 долл. США х 3 000 единиц (продукт 1) +

18 долл. США х 1 667 единиц (продукт 2) = 105 006 долл. США.

Как видно из сопоставления маржинальных прибылей, полученных при помощи двух описанных производственных стратегий, использование правильного метода принятия решения может оказать весьма позитивное воздействие на ре­зультаты деятельности компании, и сущность данного подхода состоит в определении (ранжи­ровании) прибыльности по ограниченному фак­тору (ресурсу).

В данном случае был только один лимитирую­щий фактор, на практике же существует ситуация, когда большинство компаний функционирует в ус­ловиях двух или более лимитирующих факторов. В тех случаях, когда на компании воздействует более одного лимитирующего фактора, руковод­ство компании должно решать, каким образом рас­пределить ограниченные ресурсы на различные виды продукции или услуг так, чтобы максималь­но повысить результаты деятельности.

Линейное программирование является математи­ческим методом, разработанным для помощи руко­водству компании в распределении ограниченных ресурсов компании, которое производит для реализа­ции более одной единицы затрат и функционирует в условиях двух или более лимитирующих факторов.

Процесс линейного программирования имеет три стадии:

• построение модели;
• решение модели;
• анализ решения.

Построение модели линейного программирова­ния предусматривает:

• определение переменных значений;
• определение целевой функции и создание урав­нения;
• определение ограничений и создание уравне­ний.

Целевая функция - цель, которой старается достичь менеджер.

В цехе компании решено установить дополни­тельное оборудование, для размещения которого выделено 10 м2. На приобретение оборудования предприятие может израсходовать 10 000 долл. США, при этом оно может купить оборудование двух видов. Комплект оборудования вида I стоит 1000 долл. США, а комплект вида II - 3 000 долл. США. Приобретение одного комплекта оборудования вида I позволяет увеличить выпуск продукции в смену на 2 единицы, а одного комплекта оборудо­вания вида II - на 4 единицы. Зная, что для уста­новки одного комплекта оборудования вида I тре­буется 2 м2, а оборудования вида II -1 м2, опреде­лить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.

Составим математическую модель задачи. Предположим, что предприятие приобретет X комплектов оборудования вида I и У комплектов обо­рудования вида II. Тогда переменные Х и Y должны удовлетворять следующим неравенствам:

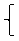                                                                2х + у ≤ 10

1000х + З000у ≤10000

Если компания приобретет указанное количество оборудования, то общее увеличение выпуска про­дукции составит: 2х + 4у max.

По своему экономическому содержанию пере­менные Х и У могу принимать лишь целые неотрицательные значения, то есть X, У ≥ 0.

Теперь решим систему линейных уравнений:

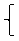                                                                2х + у ≤ 10

1000х + З000у ≤10000

1.Разделим второе уравнение системы на 1 000 и умножим первое уравнение на 3. Получаем сле­дующую систему уравнений:

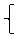                                                                  6х+3у = 30

х+3у = 10

2.Теперь вычтем из первого уравнения второе уравнение и получим:

5х = 20, где х = 4.

3. В уравнение 2х + у = 10 подставим найден­ное значение X и решим уравнение уже с одним неизвестным:

2x4 + у= 10, тогда у =2.

В соответствии с этим планом компании следу­ет приобрести четыре комплекта оборудования вида I и два комплекта оборудования вида II. Это обеспечит компании при имеющихся у него огра­ничениях на производственные площади и денеж­ные средства максимальное увеличение выпуска продукции, равное 16 единицам в смену.

В зависимости от количества переменных в уравнении целевой функции можно применять раз­ные методы решений.

Решение - это выбор альтернативы. Принятие решений - связующий процесс, необходимый для выполнения любой управленческой функции.

Запрограммированные решения, типичные чаще всего для повторяющихся ситуаций, принимаются с соблюдением конкретной последовательности этапов. Новые или сложные ситуации требуют незапрограммированных решений, в этом случае руководитель сам выбирает процедуру принятия решений.

Решения могут приниматься с помощью интуиции, суждения или методом рационального разрешения проблем. Последний способствует повышению вероятности принятия эффективного решения в новой сложной ситуации.