Преемственность планов в системе скользящего планирования: математическая постановка задачи и алгоритм решения

Как было показано в [2], содержание данной проблемы состоит в следующем. Плановый период произвольного плана имеет временную структуру (состоит из s подпериодов длительностью Dti, iÎ{1, …,s}). Пусть предыдущий план известен, т.е. был рассчитан к началу первого подпериода [– Dt1, 0] предыдущего планового периода. Тогда по истечении времени Dt1 в соответствии с принципом скользящего планирования план должен быть пересчитан на весь плановый период указанной выше временной структуры, начиная с подпериода [0, Dt1] с учетом фактического хода выполнения плана, изменения плановых заданий плана вышестоящего уровня, параметров внешней и внутренней среды предприятия, имевших место в течение подпериода [–Dt1, 0].

Очевидно, плановые периоды обоих планов (предыдущего и текущего) имеют общую часть – период [0, 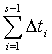]. Принцип преемственности планов предполагает, что при построении текущего плана необходимо стремиться к обеспечению максимально возможного подобия плановых показателей в указанный период.

Авторами настоящего исследования осуществлена математического постановка задачи оптимального планирования, обеспечивающая реализацию принципа преемственности, которая имеет следующие структуру и особенности.

В данной модели предполагаются заданными сетевой граф работ (мероприятий), которые могут быть включены в план текущего планового периода; возможные исполнители (структурные подразделения предприятия) каждой такой работы; длительность выполнения работ каждым из альтернативных исполнителей и затраты производственных ресурсов, включая трудовые, на их выполнения; предельные сроки выполнения отдельных работ; запасы производственных ресурсов у исполнителей и предприятия в целом; лимиты на использование производственных ресурсов, установленные планом вышестоящего уровня; план предшествующего планового периода и др.

Математическая постановка данной задачи осуществлена в терминах булевого программирования, в которой искомыми переменными являются элементы матрицы X размерности m´t´n, где xijk=1, если начало выполнения работы вида i, iÎ{1, …, m} исполнителем k, kÎ{1, …, n} назначено на подпериод j, jÎ{1, …, t} планового периода, и xijk=0 в противном случае.

Зная значения указанных переменных для всех включенных в план работ, легко определить периоды выполнения и сроки окончания работ в разрезе исполнителей, а также затраты каждым из них и предприятием в целом соответствующих ресурсов.

При этом допустимым является такой план x, который удовлетворяет ограничениям следующих видов:

ограничениям на порядок выполнения работ (определяемым сетевым графом, который задан в модели матрицей смежности);
ограничениям на сроки окончания отдельных работ (задаваемым планом вышестоящего уровня);
ограничениям на назначение работ исполнителям (в модели с этой целью использована булева матрица возможностей выполнения работ исполнителями);
ограничениям на использование производственных возможностей и производственных ресурсов исполнителей в пределах имеющихся у исполнителей "запасов";
ограничениям на лимиты использования производственных ресурсов исполнителями (установленным планом вышестоящего уровня).

Оптимальный считается план, обеспечивающий экстремум заданного экономического синтетического показателя F и характеризующийся минимально возможными отклонениями от значений соответствующих показателей предыдущего плана – невязками.

К числу таких показателей, на основе которых в модели формируются невязки текущего плана, отнесены следующие показатели:

сроки начала работ (в случае их сдвига во времени вперед);
величины временного сдвига начала таких работ;
назначение работ (в случае назначения другим исполнителям);
затраты ресурсов (в случае превышения значений, установленных предыдущим планом).

В рассматриваемой постановке использован критерий оптимальности планов смежных временных периодов следующего типа:

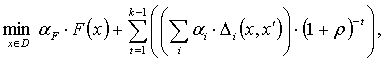
где x, x' – текущий и предыдущий планы, xÎD, D – множество допустимых планов; F – синтетический экономический показатель "качества плана" (взятый с нужным знаком); Di – величина невязки типа i; ai –коэффициент значимости (весомости) невязки типа i, ai³0, aF – коэффициент значимости экономического показателя aF, aF³0; r – ставка "дисконтирования" невязок (с помощью дисконтирования невязок обеспечивается учет в критерии оптимальности неравнозначности разновременных отклонений показателей текущего плана от показателей предыдущего плана).

Анализ математической структуры изложенной выше задачи показал, что данная задача не относится к задачам стандартного типа, для которых имеются точные алгоритмы решения. В частности, это обусловлено тем, что функции затрат ресурсов для каждого подпериода планового периода являются разрывными. Попытки ее сведения к стандартным постановкам оптимизационных задач, решаемых с помощью инструментов, содержащихся в пакете Matlab (непрерывным задачам нелинейного программирования, дискретным постановкам целочисленного программирования и целочисленного булевого программирования) продемонстрировали невозможность эффективного решения этих задач с помощью алгоритмов, реализованных в данном пакете.

Авторами настоящего исследования разработан и реализован средствами программирования Matlab алгоритм приближенного решения указанной оптимизационной задачи, основанный на идеях метода Монте-Карло. Установлено в результате решения большого числа контрольных задач, что использование в качестве шаблона при генерации случайных планов плана предыдущего планового периода, а также нормального закона распределения случайных значений показателей плана вместо равномерного на несколько порядков повышает количество допустимых планов в процедуре статистических испытаний, а алгоритм в целом является достаточно эффективным инструментом решения задач подобного типа.

К числу преимуществ методов Монте-Карло как инструмента решения оптимизационных задач является их индифферентность к числу критериев оптимальности, что позволяет использовать соответствующие алгоритмы для решения многоцелевых задач без существенных изменений.

Рассмотренная авторам настоящем исследовании задача оптимального планирования применительно к проблеме стратегического иерархического планирования реструктуризации промышленных предприятий с учетом принципа преемственности планов по своей сути является задачей многокритериальной оптимизации, что делает соответствующую ее постановку актуальной первоочередной задачей для дальнейших исследований, позволяющей, как минимум, снять вопрос об обоснованности свертки разнокачественных показателей плана, как это имело место в приведено выше критерии оптимальности.

Литература:

1. Козырь-Чепурная М.А. Временной аспект согласования стратегических планов реструктуризации предприятий в системах иерархического планирования / М.А. Козырь-Чепурная // Научная индустрия европейского континента – 2013 : IX междунар. науч.-практ. конф., 27 ноября – 15 декабря 2013 г. – Прага, 2014. – С. 102-108.

2. Козырь-Чепурная М.А. О структурных взаимосвязях стратегических планов в системе многоуровневого иерархического планирования реструктуризации предприятий / М.А. Козырь-Чепурная // Бизнес Информ. – 2015. – № 2. – С. 241-248.

3. Козырь-Чепурная М.А. Согласование планов в системе скользящего планирования реструктуризации предприятий: временной аспект / М.А. Козырь-Чепурная // Наука и образование без границ – 2013 : IX междунар. науч.-практ. конф., 7-15 декабря 2013 года. – Przemyshl, 2013. – V. 9. – S. 79-83.

4. Шпак С.А. Концепция непрерывного скользящего иерархического планирования реструктуризации предприятия / С.А. Шпак // Вісник Хмельницького національного університету. – 2013. – № 3. – Т. 2. Економічні науки. – С. 177-182.