Магистрант  Турсынбеков Т.,  проф., д.э.н.Ертаев К.

Таразский государственный университет им. М.Х.Дулати,  г. Тараз

Оптимизация распределения инвестиции в экономике промышленности

Математические модели имеют следующие виды:

модель формирования мультипликативного эффекта горнодобывающей промышленности:

У1 =  -1,97615E-08*Х1^3 +  0,000434256*X1^2  -1,794287742 *X1 +1174,818237, где: У1 - мультипликативный эффект  (прирост объема производства) горнодобывающей  промышленности, млн.тг.;

Х1 - прирост инвестиции в основной капитал горнодобывающей промышленности, млн.тг.

модель формирования мультипликативного эффекта обрабатывающей промышленности:

У2 =  -1,37791E-08 *Х2^3 + 0,000808929*X2^2 - 10,34311551 *X2 + 3008,12318,

У1 =  -1,97615E-08*Х1^3 +  0,000434256*X1^2  -1,794287742 *X1 +1174,818237, где: У2 - мультипликативный эффект  (прирост объема производства) обрабатывающей  промышленности, млн.тг.;

уравнение тренда прироста инвестиций в основной капитал промышленности

У3 = 0,242384797 *t^3 + 4525,047294*t^2-17582,62648  *t +18571,46429 ,

где: У3 - прирост инвестиции в основной капитал промышленности;

t-  фактор времени, годы.

На основе данных уравнений составляем систему уравнений

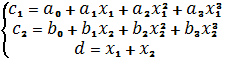
Для решения данной задачи используем метод множителей Лагранжа.  Функция Лагранжа имеет вид

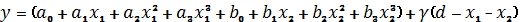
Найдем   частные производные функции  по 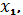 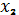  и    и 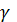приравняем их к нулю. Получили следующую систему уравнений:

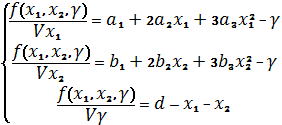
Решая систему, найдем: x1; x2; 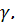   значение мультипликативного эффекта в экономике промышленности Жамбылской области. (см.табл.1 )

Значение определителя, составленного из вторых частных производных функций  по  х1,х2, (см.табл.2 ) рассчитывается по следующей формуле:

(а2 +3*а3*х1)*(в2 +3*в3*х2)

Если оно имеет положительное значение, то считается, что функция действительно имеет экстремум.

По теореме о достаточном условии существования условного экстремума функция   в точке Х1, действительно имеет экстремум. Если значение уравнения а2 + 3*а3*х1 имеет   отрицательное значение, то в этой точке х1 функция имеет условный максимум. И наоборот. Если оно имеет положительное значение, то функция в точке х1 - условный минимум. (см.табл.2 )

Прогнозные значения  инвестиции в основной капитал промышленности  определялись по трендовому методу, а распределение инвестиции  по структурным элементам  промышленностями проводилось по функции Лагранжа. В результате чего оптимально распределялись инвестиции в основной капитал среди горнодобывающей и обрабатывающей промышленностей, что эффекты на прогнозируемый период имеют тенденции к росту. (см.табл.3)

Так, например, для получения максимального мультипликативного эффекта в экономике промышленности Жамбылской области в 2014г необходимо прирост инвестиций в сумме 17828,46 млн.тг.  распределить в  сумме 20,68748 млн.тг.  в горнодобывающую промышленность, а в сумме 17807,78 млн.тг.  в обрабатывающую промышленность. При этом мультипликативный эффект от рационального распределения инвестиции на развитие экономики промышленности Жамбылской области составляет   8670,434 млн.тг. По данным таблиц 3 можно  не только  определить прогнозные значения экономики промышленности, но и  регулировать их на основе разработки и реализации экономической политики  в рамках Жамбылской области.

Преимуществами в описании формировании мультипликативного эффекта обладают динамические модели, позволяющие не только определять основные показатели развития экономики промышленности , но и получать представление о том,  за счет каких факторов и как будет формироваться траектория экономического развития.

Разработанный нами  подход к анализу и прогнозирования  формирования мультипликативных эффектов может применяться для экспертных оценок при обсуждении налоговой и тарифной политики, а также при определении значимости конкретных крупных инвестиционных проектов. Оценки возможного мультипликативного эффекта от реализации инвестиционного проекта могут оказаться полезными для представителей бизнеса и государства при определении возможных объемах административной или финансовой поддержки со стороны государства

Литература:

1.Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия = Applied Regression Analysis. — 3-е изд. — М.: «Диалектика», 2007. — С. 912. — ISBN 0-471-17082-8

2.Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа = Methoden der Korrelation - und Regressiolynsanalyse. — М.: Финансы и статистика, 1981. — 302 с.

3.  Радченко Станислав Григорьевич, Методология регрессионного анализа: Монография. — К.: «Корнийчук», 2011. — С. 376. — ISBN 978-966-7599-72-0