ст. преподаватель кафедры высшей математики Бейсеналина С.Т.

Карагандинский экономический университет Казпотребсоюза, Казахстан.

Регрессионная модель спроса

y

433

616

900

1113

1305

1488

1914

2411

x1

628

1577

2659

4796

5926

7281

9350

18807

x2

1,5

2,1

2,7

3,2

3,4

3,6

3,7

4,0

3,7

Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание от душевого дохода семей, она выражается линейной  функцией вида

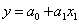
Параметры уравнения находятся в результате решения системы нормальных уравнений, которая в свою очередь формируется с применением метода наименьших квадратов, предложенного французским математиком Лежандором. Сумма квадратов отклонений должна быть минимальна  согласно методу наименьших отклонений, т.е.

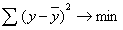
Система нормальных уравнений для рассматриваемого случая имеет вид:

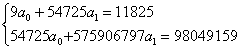
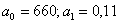
уравнение регрессии имеет вид

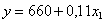
Направление связи между у и х1определяет знак коэффициента регрессии. В нашем случае связь является прямой. Теснота этой связи определяется коэффициентом корреляции, чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем случае

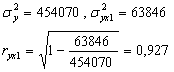
Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.

Величина 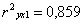 называется коэффициентом детерминации и показывает долю изменения результативного признака под воздействием факторного признака, т.е. 86% изменения расходов на питание можно объяснить фактором душевого дохода. 

Теперь рассмотрим двухфакторную линейную модель зависимости расходов на питание от душевого дохода семей и размера семей.

Многофакторный корреляционно – регрессионный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов.

В нашем случае модель имеет вид

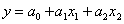
Параметры, находятся в результате решения системы нормальных уравнений

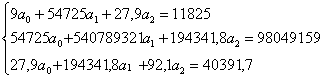
Решая систему, получим 

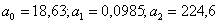
Тогда уравнение регрессии имеет вид

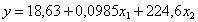
Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции. После этого вычисляется коэффициент множественной корреляции:

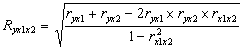
который колеблется в пределах от 0 до 1; чем ближе он к единице, тем  в большей степени учтены факторы, влияющие на результативный признак. А в нашем примере Ryx1x2  = 0, 983, что выше значения коэффициента корреляции в случае однофакторной регрессии. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень тесной.

Величина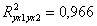 называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака  под воздействием факторных признаков, т.е.97% изменения расходов на питание можно объяснить факторами душевого дохода и размера семей.

Задача анализа тесноты связи между результативным и одним из факторных признаков при неизменных значениях других факторов решается в многофакторных моделях при помощи частных коэффициентов корреляции. Так частный коэффициент корреляции между результативным признаком и факторным признаком при неизменном значении факторного признака рассчитывается по формуле

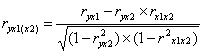
где используются парные коэффициенты корреляции. Для рассматриваемого примера частные коэффициенты расходов на питание от душевого дохода и размера семей составляют , 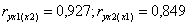т.е. теснота связи между расходами на питание  и одним из исследуемых факторов при неизменном значении другого весьма велика.

Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации, показывающие долю вариации результативного признака под действием  одного из факторов при неизменном значении другого фактора. В нашем примере 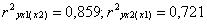следовательно, влиянием душевого при неизменном размере семьи объясняется почти 86%  изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.

Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.

В случае линейной двухфакторной модели частные коэффициенты эластичности рассчитываются по формулам:

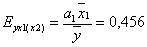
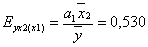
Это означает, что при увеличении душевого дохода на 1% и неизменном размере семьи расходы на питание увеличатся на 0,456%, а увеличение (условное) на один процент размера семьи при неизменном душевом доходе приведет к возрастанию расходов на питание на 0,530%.