Т.Н. Агапова
доктор экономических наук, профессор,
При осуществлении сопоставлений состояния нескольких территорий необходимо учитывать смысл каждого индикатора, в частности положительное или отрицательное влияние на состояние территории оказывает то или иное явление, результат действия которого измеряется значением индикатора. Так, значения индикаторов, отражающих объемы выбросов загрязняющих веществ в атмосферный воздух, численность пострадавших при несчастных случаях на производстве, число убыточных предприятий и организаций, уровень заболеваемости населения являются факторами, имеющими отрицательное влияние на значение комплексной оценки состояния территории, снижающее ее величину; значения индикаторов, отражающих объемы инвестиций предприятий в природоохранную деятельность, численность врачей и больничных учреждений, уровень образованности населения, объемы производства ВРП (ВВП) являются факторами, которые имеют положительное влияние на значение комплексной социальной, экологической и экономической оценки состояния территории, увеличивая в комплексе ее значение.
В предлагаемой нами методике сравнительной комплексной оценки состояния территорий, основанной на процедуре многомерного сопоставления совокупности территорий по системе индикаторов социального, экологического и экономического состояния, можно выделить следующие основные этапы:
1) определение и обоснование, исходя из целей исследования, круга территорий, охватываемых комплексной сравнительной оценкой;
2) отбор показателей, являющихся индикаторами состояния территории по выделенным проблемно-содержательным блокам;
3) нормирование (стандартизация) значений индикаторов, включенных в основу оценки состояния сравниваемых территорий, которое применяется чаще всего с целью нивелирования абсолютных величин, их разноразмерности, а в нашем случае для снижения степени вариации значений сравниваемых индикаторов. При этом предлагаемый нами способ нормирования базируется на определении «наиболее благоприятного» и «наименее благоприятного» значений индикатора. Такой подход обоснован тем, что при нормировании и сопоставлении значений индикаторов смысл максимальности или минимальности значения индикатора не всегда отражает соответственно положительное или отрицательное состояние территории, это зависит от смысла или природы самого индикатора. Предлагаемая нами формула нормирования значений индикаторов имеет вид:
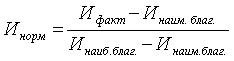 , (1)
, (1)
где 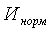 – нормированное значение индикатора;
– нормированное значение индикатора;
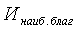 – наиболее благоприятное значение индикатора;
– наиболее благоприятное значение индикатора;
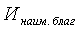 – наименее благоприятное значение индикатора.
– наименее благоприятное значение индикатора.
При определении «наиболее благоприятного» и «наименее благоприятного» значений индикаторов следует исходить из следующих принципов:
4) расчет частных сравнительных оценок по каждому индикатору для каждой территории и представление результатов сопоставлений в виде оценочных таблиц, строящихся для каждого индикатора в виде квадратной матрицы, следующего вида:
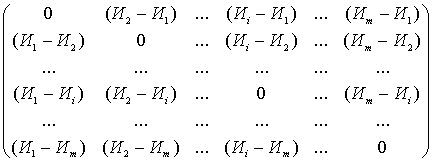 , (2)
, (2)
где т – число сравниваемых территорий;
5) сведение результатов расчета частных оценок по индикаторам в итоговую оценочную таблицу, отражающую комплексную сравнительную оценку состояния рассматриваемых территорий, путем суммирования значений частных сравнительных оценок в соответствии с их местом в матрице по всей системе индикаторов для каждой территории:
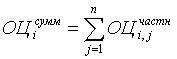 , (3)
, (3)
где 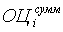 – суммарное значение оценки для i - ой территории;
– суммарное значение оценки для i - ой территории;
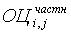 – значение частной сравнительной оценки для i-ой территории по j – ому индикатору;
– значение частной сравнительной оценки для i-ой территории по j – ому индикатору;
п – число индикаторов, включенных в основу оценки
и последующее нахождение значения обобщающей оценки для каждой территории:
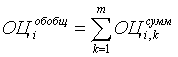 , (4)
, (4)
где 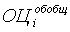 – значение обобщающей оценки для i-ой территории;
– значение обобщающей оценки для i-ой территории;
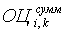 – суммарное значение сравнительной оценки для i-ой территории в k-ой строке итоговой оценочной таблицы;
– суммарное значение сравнительной оценки для i-ой территории в k-ой строке итоговой оценочной таблицы;
т – число строк в итоговой оценочной таблице, равное числу сравниваемых территорий;
6) анализ полученных обобщающих сравнительных оценок территорий. С целью сделать процесс сравнительной оценки визуально более понятным и наглядно представляющим соотношение полученных значений, выполнить вычисление относительных значений оценок следующим образом:
а) приведение полученных обобщающих оценок к неотрицательному виду согласно формуле:
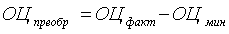 , (5)
, (5)
где 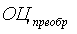 - преобразованное значение оценки (приведенное к неотрицательному виду);
- преобразованное значение оценки (приведенное к неотрицательному виду);
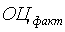 - фактически полученное значение суммарной оценки;
- фактически полученное значение суммарной оценки;
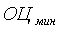 - минимальное из всех полученных значений оценок.
- минимальное из всех полученных значений оценок.
б) сравнение полученных значений преобразованных оценок с максимальным значением в их совокупности и выражение результата сравнения в процентах:
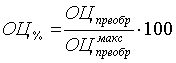 (6)
(6)
7) анализ и сравнение относительных комплексных оценок состояния территории, имеющих процентное выражение, их графическое представление и интерпретация.
Очевидно, что при таком подходе к вычислению комплексной оценки, максимально возможное ее значение будет равно 100% и может быть интерпретировано как наиболее благоприятное в комплексе социальное, экологическое и экономическое состояние территории в сравнении с состояниями других территорий; минимально возможное значение оценки равно 0%, что указывает на неблагоприятные условия, сложившиеся в экономике территории, ее экологическое неблагополучие и низкий уровень жизни общества в сравнении с другими территориями.
8) изучение вклада значений индикаторов каждого блока в формирование комплексной оценки возможно путем расчета блоковых относительных оценок состояния территорий по выше описанной методике, базируясь на ранее рассчитанных частных оценках индикаторов по выделенным трем блокам.
9) анализ адекватности полученных значений комплексных оценок состоянию сравниваемых территорий.
Оценить степень адекватности значения оценки предлагаем уровнем вариации блоковых оценок, исходя из нижеследующего: чем ниже уровень вариации значений оценок по блокам, тем получаемое значение комплексной оценки, охватывающей все индикаторы, будет более типичным, а значит выражающим то общее, что присуще состоянию территории.
В качестве показателя, измеряющего уровень вариации блоковых оценок, предлагаем коэффициент вариации, для расчета значения которого необходимо исчислить средние значения и стандартные отклонения по совокупности блоковых оценок для каждой территории:
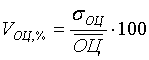 , (7)
, (7)
где 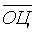 - среднее значение блоковых оценок;
- среднее значение блоковых оценок;
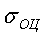 - стандартное отклонение блоковых оценок.
- стандартное отклонение блоковых оценок.
Данная формула коэффициента вариации является классической при измерении степени колеблемости значений некоторого количественного признака и характеристики устойчивости их среднего значения. Однако в нашем случае проявились некоторые особенности и трудности применения данной формулы в силу того, что:
- во-первых, значения анализируемого признака представляют собой относительные величины, имеющие процентное выражение, что влияет на выбор способа исчисления таких обобщающих статистических характеристик как среднее значение
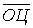 и стандартное отклонение
и стандартное отклонение 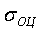 , а также делает неопределенной интерпретацию получаемого значения коэффициента вариации, который будет представлять собой относительную величину второго порядка;
, а также делает неопределенной интерпретацию получаемого значения коэффициента вариации, который будет представлять собой относительную величину второго порядка;
- во-вторых, объем совокупности значений осредняемого признака (число значений блоковых оценок) достаточно мал (всего три значения), что, очевидно, приведет к не типичности обобщающих характеристик и высокому значению коэффициента вариации.
Для определения адекватности комплексных оценок необходимо расширить совокупность результатов сравнения состояния территорий, охватив методикой оценки не только совокупность индикаторов статике, но ввести в исследование их значения в динамике.
Исчисление для каждого периода времени и каждой территории среднего значения из блоковых оценок, а также сопоставление значений этих средних и значений комплексных оценок для одного и того же периода времени, могут привести к следующим результатам:
- значения комплексной оценки и средней из блоковых оценок не равны между собой. Исключением является частный случай, когда значения оценок по блокам равны друг другу и соответственно равны значению комплексной оценки;
- величина стандартного отклонения значений блоковых оценок от значения комплексной оценки во всех случаях, кроме частного случая, описанного выше, больше величины стандартного отклонения значений блоковых оценок от их среднего значения.
Именно данные выводы легли в основу предлагаемого нами способа определения степени адекватности комплексной оценки действительному состоянию территории.
Суть состоит в том, что степень вариации значений блоковых оценок относительно значения комплексной оценки выше, чем относительно среднего значения, найденного по совокупности этих блоковых оценок, за исключением частного случая, когда блоковые и комплексная оценки равны между собой и вариация в таком случае отсутствует.
В результате была сформулирована гипотеза о том, что значение комплексной сравнительной оценки будет адекватно состоянию территории, если оно не существенно будет отличаться от среднего значения блоковых оценок, а значит, величина стандартного отклонения значений блоковых оценок от значения комплексной оценки будет не существенно больше величины стандартного отклонения значений блоковых оценок от их среднего значения.
Существуют статистические критерии, позволяющие проверить справедливость гипотезы о равенстве дисперсий двух совокупностей, например, критерий Фишера. Применение именно этого критерия в нашем случае уместно в силу того, что мы стремимся сравнить межблоковую вариацию значений оценок относительно значения комплексной оценки и среднего значения оценок по блокам.
Сформулируем задачу применения данного критерия для проверки адекватности значения комплексной сравнительной оценки состоянию территории.
Пусть по совокупности индикаторов состояния территории вычислена на основе предложенной нами методики комплексная сравнительная оценка 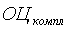 и блоковые оценки
и блоковые оценки 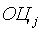 , где j – индекс, означающий номер блока в основе оценки, причем j = 1, 2, …, k, где k – число блоков, выделенных в основе оценки состояния территории. Пусть также исчислено среднее значение из блоковых оценок
, где j – индекс, означающий номер блока в основе оценки, причем j = 1, 2, …, k, где k – число блоков, выделенных в основе оценки состояния территории. Пусть также исчислено среднее значение из блоковых оценок 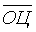 по формуле:
по формуле:
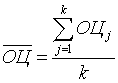 (8)
(8)
и стандартные отклонения значений блоковых оценок от значения комплексной оценки 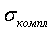 и от их среднего значения
и от их среднего значения 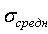 по формулам:
по формулам:
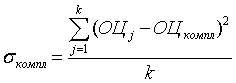 , (9)
, (9)
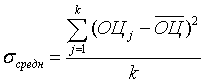 , (10)
, (10)
на основе значений которых вычислены дисперсии 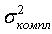 и
и 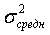 .
.
Проверим нулевую гипотезу о равенстве дисперсий:
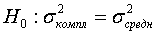
относительно конкурирующей гипотезы:
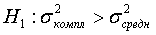 ,
,
используя статистический критерий Фишера.
Вычислим статистику критерия по формуле:
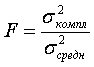 , (11)
, (11)
где значение дисперсии 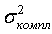 стоит в числителе формулы критерия, т. к. оно больше значения дисперсии
стоит в числителе формулы критерия, т. к. оно больше значения дисперсии 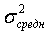 , за исключением частного случая, когда
, за исключением частного случая, когда 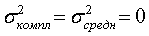 , возникающего при совпадении значений комплексной и блоковых оценок. Очевидно, что для частного случая необходимости применения критерия нет, т. к.
, возникающего при совпадении значений комплексной и блоковых оценок. Очевидно, что для частного случая необходимости применения критерия нет, т. к. 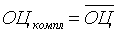 .
.
При формировании критерия отклонения (принятия) гипотезы 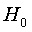 учтем тот факт, что распределение статистики F является не симметричным и сформулированная конкурирующая гипотеза
учтем тот факт, что распределение статистики F является не симметричным и сформулированная конкурирующая гипотеза 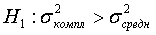 является правосторонней. В таком случае гипотеза
является правосторонней. В таком случае гипотеза 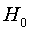 отвергается, если
отвергается, если
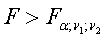 , (12)
, (12)
где 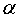 - уровень значимости;
- уровень значимости;
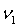 ,
, 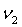 - число степеней свободы межблоковой вариации значений индикаторов, которые в нашем случае равны
- число степеней свободы межблоковой вариации значений индикаторов, которые в нашем случае равны 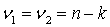 , где n – число индикаторов, включенных в основу оценки состояния территорий, k – число блоков, выделенных в основе оценки;
, где n – число индикаторов, включенных в основу оценки состояния территорий, k – число блоков, выделенных в основе оценки;
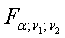 - табличное значение критерия Фишера.
- табличное значение критерия Фишера.
Если условие (12) не выполнено, то гипотеза 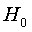 не отвергается, а значит, на уровне значимости
не отвергается, а значит, на уровне значимости 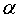 можно утверждать, что для данной совокупности сравниваемых территорий вариация значений блоковых оценок относительно значения комплексной оценки
можно утверждать, что для данной совокупности сравниваемых территорий вариация значений блоковых оценок относительно значения комплексной оценки 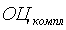 не существенно выше их вариации относительно своего среднего значения
не существенно выше их вариации относительно своего среднего значения 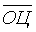 и найденная комплексная оценка адекватна состоянию территории.
и найденная комплексная оценка адекватна состоянию территории.
Список использованных источников:
1. Агапова Т.Н. Статистические показатели изменения системы связей. // Математико-статистический анализ социально-экономических процессов. Выпуск № 9, М.: МЭСИ, 2012.
2. Агапова Т.Н., Шихова О.А. Социо-эколого-экономическое развитие территорий и регионов мира. // Региональная экономика. М.: Финансы и кредит, №11 (50), 2007.
