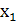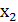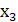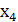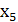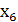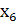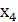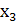К.т.н. Павлова Т.А., к.э.н Уварова М.Н.

ФГБОУ ВПО «Орловский государственный аграрный университет», Россия

Применение симплексного метода для оптимизации струк-туры посевных площадей

Математические методы позволяют обнаружить и выявить закономерности, складывающиеся в сельском хозяйстве, обнаружить узкие места в производстве, обосновать наиболее рациональное распределение имеющихся ресурсов между возможными способами производства, сравнить отдельные варианты планов.В состав математической модели входят соотношения, отражающие условия, которым должно удовлетворять решение (план) данной задачи (так называемая система ограничений), а также функция, в математической форме выражающая поставленную цель с точки зрения выбранного критерия оптимальности (так называемая целевая функция). Поиск оптимального плана с математической точки зрения представляет собой определение такого набора числовых значений неизвестных, удовлетворяющих ограничительным условиям задачи, при этом целевая функция достигает экстремальной величины (максимума и минимума) [1,4].

Наиболее общим и универсальным является симплексный метод, который позволяет находить оптимальное решение всех задач линейного программирования. Решение задачи симплексным методом проводится по  следующей схеме:указывается способ вычисления начального допустимого или опорного решения;с помощью признака оптимальности проверяется, не является ли это решение оптимальным;по выбранному начальному решению строится другое, более близкое к оптимальному [2,3].Рассмотрение примеров прикладного характера позволяет будущему специалисту на практике применить приобретенные теоретические знания.  Например, необходимо найти оптимальное сочетание посевов трёх культур: капусты, картофеля и многолетних трав на сено при условии, что в хозяйстве:850 га пашни,50000 чел.-дней труда,5000 т органических удобрений.Затраты этих ресурсов, а также выход валовой продукции в денежном выражении в расчёте на 1 га культур приведены в таблице 1. Критерий оптимальности - максимум валовой продукции в денежном выражении.

Таблица 1

Затраты ресурсов на 1 га возделывания культур

Обозначим искомые посевные площади капусты x1, картофеля x2, многолетних трав x3 (га). Тогда математическая модель задачи может быть сформулирована так: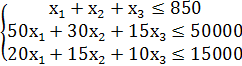  (1)

Z = 1000 . x1 + 800 . x2 + 200 . x3®max

Приведя систему (1) к каноническому виду, получаем:

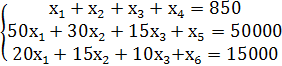       (2)

Z = 1000 . x1 + 800 . x2 + 200 . x3®max

В системе (2) дополнительные неотрицательные переменные x4, x5, x6  означают соответственно недоиспользование ресурсов земли, труда и удобрений.  Исходные данные и значение целевой функции заносятся в симплексную таблицу.

Таблица 2

Решаем задачу  симплексным методом до тех пор, пока в строке с целевой функцией не будет отрицательных коэффициентов (табл. 3).

Результаты решения задачи выписываются из таблицы 3, из столбца базисных переменных и столбца свободных членов: x1=450, x2=400, x5=15500, Z=770000. Следовательно, при принятых в задаче условиях максимальная величина валовой продукции может составить 770000 рублей. Для этого необходимо, чтобы посевная площадь капусты составила 450 га, картофеля 400 га. Для принятого критерия оптимальности посев многолетних трав оказался невыгодным и не вошел в оптимальное решение (x3=0). Подставляя полученные значения переменных в систему (1) осуществим проверку решения:

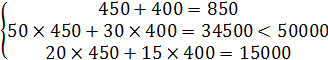
Z=1000 .450+800 . 400=770000

Полученные результаты свидетельствуют о том, что из трёх ресурсов, имеющихся в хозяйстве, два (земля и удобрения) используются полностью, трудовые ресурсы недоиспользованы в размере 15500чел.- дней.

Литература:

1. Акулич, И. Л. Математическое программирование в примерах и задачах. Учебное пособие / И.Л. Акулич. - 3-изд. М.: Лань, 2011. – 352 с. ISBN: 978-5-8114-0916-7

2. Красс, М.С. Математика в экономике Математические методы и модели. Учебник для бакалавров / М.С. Красс, Б.П. Чупрынов. - 2 изд. М.: Юрайт, 2013. — 541 с. ISBN:978-5-9916-3020-7

3. Петров А. В. Вычислительная техника в инженерных и экономических расчётах.– М.: Высшая школа, 1991.

4. Тунеев М. М., Сухоруков В. Ф. Экономико-математические методы в организации и планировании сельскохозяйственного производства.– М.:Финансы и статистика, 1986.

5. Курносов А. П. Вычислительная техника и программирование.– М.: Финансы и статистика, 1991.

6. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: Учеб. Пособие. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2005. - 432 с.