Анализ и прогноз валового внутреннего продукта Сибирского федерального округа

д.т.н., профессор. Пиль Э.А., Санкт-Петербургский государственный морской технический университет, Россия

Для анализа и прогноза ВВП Сибирского федерального округа была использована Линия Тренда, а также программа «РЕГРЕССИЯ». Анализ проводился по статическим данным за период с 2005 по 2010 гг. Значения ВВП за 2011 год был взят для анализа погрешности между статистическими и расчетными значениями.

На рис. 1 представлена полученная зависимость, из которой видно, что коэффициент корреляции здесь получился достаточно большим R2 = 0.9539, что позволит нам производить прогноз ВВП с достаточно большой точностью.

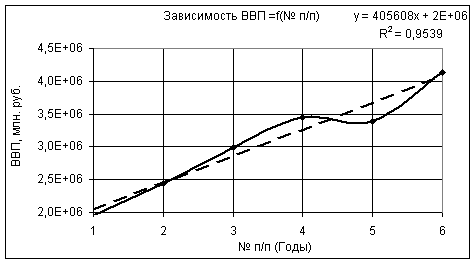
Рис. 1. Линейная зависимость.

На следующем рис. 2 представлена степенная зависимость, где полученный коэффициент корреляции также имеет достаточно высокое значение R2 = 0.9711.

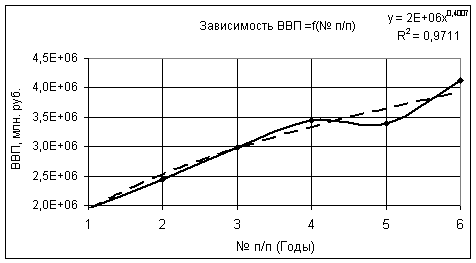
Рис. 2. Степенная зависимость.

Таблица 1. Статистические и расчетные значения ВВП Сибирского федерального округа на 2011 г, млн. руб.
п/п	Уравнение	Статистические значения	Расчетные значения	Погрешность, %
1	4795595	4839256	0,91
2	y = axb	4795595	4361750	9,05

Таблица 2. Прогноз ВВП на основе анализа с использованием Линии Тренда в Excel, млн. руб.
№ п/п	Годы	Линейная зависимость	Степенная зависимость
1	2012	5244864	4601487
2	2013	5650472	4823863
3	2014	6056080	5031877
4	2015	6461688	5227765
5	2016	6867296	5413248
6	2017	7272904	5589682
7	2018	7678512	5758157
8	2019	8084120	5919565
9	2020	8489728	6074645

В таблице 1 представлены статистические и расчетные значения ВВП, а также погрешность полученных значений. Как видно из табл. 1 линейная зависимость дает более точные значений при расчетах. Здесь на рисунках №п/п соответствует году, т.е. № 1 соответствует 2005 году и т.д.

При использовании программы РЕГРЕССИЯ был произведен корреляционно-регрессионный анализ ВВП Сибирского федерального округа по 16 различным зависимостям, которые представлены в табл. 3.

Таблица 3. Уравнения для корреляционного анализа
1.	y = a + bx	9.	y = axb
2.	y = 1/(a + bx)	10.	y = a + b∙log(x)
3.	y = a + b/x	11.	y = a + b∙ln(x)
4.	y = x/(a + bx)	12.	y = a/(b + x)
5.	y = a∙bx	13.	y = ax/(b + x)
6.	y = a∙exp(bx)	14.	y = a∙exp(b/x)
7.	y = a∙10(bx)	15.	y = a∙10(b/x)
8.	y = 1/(a + b∙exp(-x))	16.	y = a + b∙xn

Произведенные расчеты, показали, что из 16 видов уравнений можно также использовать только линейную и степенную зависимости, у которых были получены следующие коэффициенты корреляции R2 = 0,9767 и R2 = 0,9852 соответственно.

В табл. 4 представлены расчеты по прогнозу ВВП до 2020 года с использованием значений, полученных с использованием программы РЕГРЕССИЯ.

Таблица 4. Прогноз ВВП на основе анализа с использованием программы РЕГРЕССИЯ, млн. руб.
п/п	Годы	Линейная зависимость	Степенная зависимость
1	2012	5289121	4616837
2	2013	5694729	4815909
3	2014	6100337	5003375
4	2015	6505945	5180883
5	2016	6911553	5349731
6	2017	7317161	5510962
7	2018	7722770	5665429
8	2019	8128378	5813840
9	2020	8533986	5956790