Виталий Сергеевич Боровик, Виталий Витальевич Боровик
Визуализация задачи управления в пространстве 4D
Пространственное моделирование инновационно-инвестиционного процесса осуществляется на основе производственной функции. В производственную функцию вводятся дифференциалы производственных ресурсов dxi, i=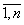 , относительно соответствующих ресурсов -
, относительно соответствующих ресурсов -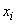 . На примере управления интегрированной экономической системой с помощью квазипреобразования Лоренца и пространства Минковского сделана попытка моделирования управления в четырехмерном пространстве, объединяющем физическое трёхмерное пространство и время.
. На примере управления интегрированной экономической системой с помощью квазипреобразования Лоренца и пространства Минковского сделана попытка моделирования управления в четырехмерном пространстве, объединяющем физическое трёхмерное пространство и время.
«Переход к идеологии системного пространственного анализа означает необходимость междисциплинарного подхода, что связано с существенными методологическими и организационными трудностями, хотя и обещает принципиальное приращение качества самого анализа. Междисциплинарные исследования при всей на первый взгляд очевидной и многообещающей продуктивности представляют собой на практике весьма трудную даже для понимания и тем более для реального воплощения форму познания». [5, cтр. 28.]
К настоящему времени наиболее эффективным экономическим аппаратом, учитывающим количественные и качественные характеристики использования ресурсов, существенно облегчающим процесс понимания экономического анализа и прогнозирования является производственная функция (ПФ)[8]. Следует признать, что ПФ опосредованно отражает влияние социальных, технологических, гуманитарных и др. аспектов поведения экономического агента[1].
Узловой раздел моделирования в системе управления инновационно-инвестиционным процессом связан с решением одной из основных задач управления – результат, достигаемый процессом должен превышать затраты [16]. Решение последней замыкается на использовании численных экономических параметров в отрыве от качественных характеристик конкретного объекта, например, [10]. К настоящему моменту отсутствует доступные модели, представляющие числовую информацию и физическое проявление процесса управления инновационно-инвестиционым процессом в виде, удобном и адекватном для зрительного наблюдения, анализа и определения оптимального варианта.
Инновационный тип развития создает предпосылки для коренного изменения структуры и содержания моделей, учитывающих взаимосвязь производственных процессов и темпов их выполнения [15, 17]. В современных условиях время как социально-экономическая категория выступает как ресурс в значительной мере определяющий цели интегрированных экономических систем (ИЭС)[5,7].
Стремление выяснить особую роль времени в развитии процессов, происходящих в ИЭС в условиях инновационного развития, приводит к ряду предположений, заслуживающих серьезного внимания [4, 20][2]. Дж. Уитроу, отстаивая мнение о реальности и объективности времени, отмечает, что: «Центральным пунктом дискуссии является статус «становления» или совершающегося, а также прошлого, настоящего и будущего; другими словами, тех черт времени, для которых не имеется пространственных аналогий» [20]. В этой связи пространственное моделирование управления с включением параметра времени в качестве четвертого измерения является весьма актуальной задачей [14].
Постановка проблемы
Функционирование современных ИЭС рассматривается как многофакторный процесс. Для наиболее точного прогнозирования влияния инновационно-инвестиционного воздействия на результаты деятельности ИЭС во времени ставится задача теснее связать труд и производственные фонды между собой и, в то же время, более рельефно выделить действие факторов в их взаимосвязи и взаимозависимости, повысить их информационную нагрузку и её разнообразие [3]. Такие требования неизбежно приводят к необходимости решения задачи управления в многомерном пространстве.
где 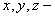 пространственные координаты, а
пространственные координаты, а 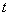 временнàя координата, с –скорость света. Эта система координат называется в физике галилеевой и соответствует инерциальной системе отсчета (и.с.о.)[3]. (В специальной теории относительности и.с.о. обычно задаются галилеевой системой координат, в классической механике – декартовой системой координат.) В исследованиях Галилея заслуживает внимания способность преобразования Галилея сохранять пространственные размеры тел и длительности физических процессов[4]. Переход между различными галилеевскими системами координат, при соответствующих и.с.о., движущихся друг относительно друга, осуществляется с помощью Лоренца преобразования [13]. Это преобразование дает возможность осуществлять пространственное отражение множества точек во времени, которое с позиций физики является преобразованием перехода от одной инерциальной системы отсчета к другой, движущейся относительно первой со скоростью V .
временнàя координата, с –скорость света. Эта система координат называется в физике галилеевой и соответствует инерциальной системе отсчета (и.с.о.)[3]. (В специальной теории относительности и.с.о. обычно задаются галилеевой системой координат, в классической механике – декартовой системой координат.) В исследованиях Галилея заслуживает внимания способность преобразования Галилея сохранять пространственные размеры тел и длительности физических процессов[4]. Переход между различными галилеевскими системами координат, при соответствующих и.с.о., движущихся друг относительно друга, осуществляется с помощью Лоренца преобразования [13]. Это преобразование дает возможность осуществлять пространственное отражение множества точек во времени, которое с позиций физики является преобразованием перехода от одной инерциальной системы отсчета к другой, движущейся относительно первой со скоростью V .
Инерциальные системы отсчета - физические модели, в которых мы можем указать хотя бы одну "неподвижную точку" (или "неподвижное тело"). При выполнении экономического анализа указать хотя бы одну неподвижную точку не составляет труда. Для примера – точка достигнутого уровня экономического развития, географические характеристики конкретного региона и др. В рассматриваемой системе временнáя координата оказывается выраженной как через временнýю, так и через пространственные координаты.
Учитывая, что преобразование Лоренца является аналогом ортогональных преобразований (или обобщением понятия движения) в евклидовом пространстве, возникает возможность связать в пространстве Минковского [18] две галилеевы системы координат рис. 1[5].
Принимая во внимание также, что система координат Галилея отличается от декартовой системы координат только приложениями системы отсчета[6] можно принять с достаточной степенью обоснованности приведенный способ визуализации четырехмерного пространства в качестве первого приближения..
Полезно отметить, что «теорию относительности часто критиковали за то, что она неоправданно приписывает центральную теоретическую роль явлению распространения света, основывая понятие времени на его законах. Положение дел, однако, примерно таково. Чтобы придать понятию времени физический смысл, нужны какие-то процессы, которые дали бы возможность установить связь между различными точками пространства. Вопрос о том, какого рода процессы выбираются при таком определении времени, несущественен. Для теории выгодно, конечно, выбирать только те процессы, относительно которых мы знаем что-то определенное. Распространение света в пустоте благодаря исследованиям Максвелла и Лоренца подходит для этой цели в гораздо большей степени, чем любой другой процесс, который мог бы стать объектом рассмотрения». [7] (Выделено авторами статьи)
Отсюда можно сделать очень важный вывод. В системе (1) с – скорость света в вакууме – константа. Для решения прикладной задачи её следует заменить на константу, которая в наибольшей мере удовлетворяет требованиям анализируемого процесса[8]. Например, можно принять максимально возможную установленную (или расчетную) производительность труда, географические условия с установленными характеристиками и др.
Целью исследования является моделирование управления инновационно-инвестиционным процессом в ИЭС, позволяющего наглядно представить результаты экономического анализа на основе визуализации четырехмерного пространства способствующего лучшему пониманию экономических процессов, а также оценки и поиску оптимального управления.
Моделирование управления инновационно-инвестиционным процессом
Эконометрические аспекты визуализации процесса управления
Главная задача – предложить теоретическую платформу, позволяющую выполнять анализ пространственного распределения, обоснование вероятных ситуаций и прогнозирование результатов инновационно-инвестиционного процесса в системе регионального управления. В качестве наиболее универсальной формы анализа функционирования ИЭС предлагается использовать ПФ типа Кобба-Дугласа, например, вида:
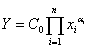 , (2)
, (2)
где Y – расчетный индекс (например, прибыль, объем ВРП, объем работ и др. в натурально-вещественном или стоимостном выражении); xi , i=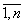 - факторы (ресурсы), влияющие на Y (в натурально-вещественном или стоимостном выражении); αi, i=
- факторы (ресурсы), влияющие на Y (в натурально-вещественном или стоимостном выражении); αi, i=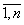 - «веса», характеризующие вклад xi в Y; C0 – коэффициент, характеризующий совокупное влияние факторов, не учтенных моделью.
- «веса», характеризующие вклад xi в Y; C0 – коэффициент, характеризующий совокупное влияние факторов, не учтенных моделью.
Рассмотрим трехмерную графическую модель (рис. 2) производственной функции (ПФ) вида (1). Функция наиболее доступна для понимания ввиду возможности ее наглядного представления в трехмерном пространстве [1, 2]. Кривые -1Y и 2Y соединяют точки с одинаковыми численными значениями ВРП. Их проекции – 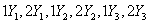 - изокванты.
- изокванты.
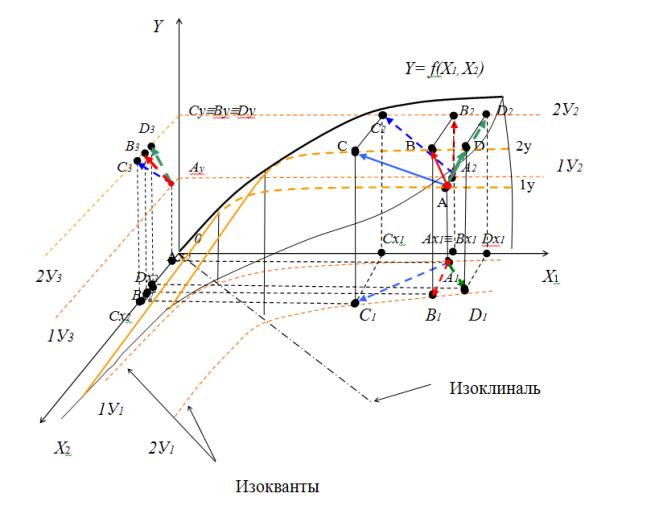
Рис. 2. Пространственная эконометрическая модель 3D на основе ПФ, отображающая поверхность с управлением, характеризуемым различными сочетаниями потребления ресурсов при перемещении с уровня 1У на 2У
Как видно на рис. 2, из точки А, характеризуемой, например, ВРП 1Y, объем ВРП 2Y может быть достигнут в конкретной ИЭС путем реализации инновационно-инвестиционного процесса бесконечным множеством сочетаний труда и прочих ресурсов. Например, точки В, С и D, показывающие некоторые варианты выхода на достижение объема ВРП, характеризуемого как 2Y. В зависимости от возможностей ИЭС, квалификации кадров, качества управления, социальных условий, качества ресурсов, цели ИЭС, задач и др. выбирается тот или иной вариант использования ресурсов.
Рассмотрим три варианта выхода с 1Y на более высокий уровень 2Y, обеспечиваемый реализацией инновационно-инвестиционного процесса. Рассмотрим векторы 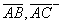 и
и 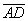 . Каждому из них соответствует свое сочетание использования ресурсов:
. Каждому из них соответствует свое сочетание использования ресурсов: 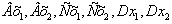 . Будем считать оптимальным с математических позиций вариант
. Будем считать оптимальным с математических позиций вариант 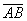 , т.к.
, т.к. 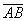 ^2У (к касательной в точке В) и является кратчайшим расстоянием между 1Y и 2Y.
^2У (к касательной в точке В) и является кратчайшим расстоянием между 1Y и 2Y.
Известно, что каждая ИЭС характеризуется индивидуальной, присущей только конкретной ИЭС системой использования ресурсов [1]. Поэтому управление, в котором в качестве критерия оптимальности принято кратчайшее расстояние между изоквантами, может рассматриваться для реальной ИЭС только как идеальный вариант.
В качестве примера рассмотрим ПФ двух ИЭС:
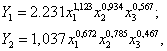
где 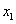 – основные средства;
– основные средства; 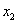 – оборотные средства;
– оборотные средства;
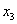 – затраты труда.
– затраты труда.
Допустим, что у этих ИЭС абсолютно одинаковые объемы ресурсов. Однако коэффициенты эластичности у первой ИЭС больше чем у второй. Это свидетельствует о том, что ресурсы у первой ИЭС используются более интенсивно, чем у второй. Кроме этого влияние факторов, не учтенных моделью -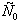 , у первой в два с лишним раза больше чем у второй. В конечном итоге получим
, у первой в два с лишним раза больше чем у второй. В конечном итоге получим 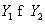 . Подчеркнем, – при совершенно одинаковых объемах затраченных ресурсов.
. Подчеркнем, – при совершенно одинаковых объемах затраченных ресурсов.
В этой связи реализацию инновационно-инвестиционного процесса в ИЭС нами предлагается рассматривать как алгебраическое введения в её ПФ некоторых дифференциалов dxi , i=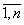 , относительно соответствующих факторов –
, относительно соответствующих факторов – 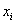 (ресурсов). Такая постановка обусловлена необходимостью осуществлять либо приращение, либо сокращение ресурсов. В частности, акад. Полтерович В.М. отмечает важность и ответственность эконометрических прогнозных расчетов и установлению связей между различными показателями в условиях инновационного развития. Даже в расчетах оценки влияния IT на темпы экономического развития при участии значительных сил ученых и специалистов были допущены серьезные просчеты [7].
(ресурсов). Такая постановка обусловлена необходимостью осуществлять либо приращение, либо сокращение ресурсов. В частности, акад. Полтерович В.М. отмечает важность и ответственность эконометрических прогнозных расчетов и установлению связей между различными показателями в условиях инновационного развития. Даже в расчетах оценки влияния IT на темпы экономического развития при участии значительных сил ученых и специалистов были допущены серьезные просчеты [7].
Например, внедрение прогрессивных технологий может способствовать увеличению основных фондов –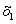 . Тогда, как правило, использование высокопроизводительных машин и механизмов способствует увеличению потребления оборотных фондов –
. Тогда, как правило, использование высокопроизводительных машин и механизмов способствует увеличению потребления оборотных фондов – 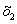 и, например, сокращению затрат на труд –
и, например, сокращению затрат на труд – 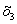 . Следовательно, в ПФ необходимо ввести:
. Следовательно, в ПФ необходимо ввести: 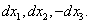 Понятно, что эффективность освоения этих дифференциалов (приращений ресурсов) может быть различной в зависимости, прежде всего, от качества управления процессом. Априори можно констатировать, что при всех прочих равных условиях введение в ПФ первой ИЭС дифференциалов ресурсов
Понятно, что эффективность освоения этих дифференциалов (приращений ресурсов) может быть различной в зависимости, прежде всего, от качества управления процессом. Априори можно констатировать, что при всех прочих равных условиях введение в ПФ первой ИЭС дифференциалов ресурсов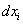 , i=
, i=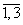 даст больший прирост
даст больший прирост 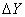 , т.к. ресурсы в первой ИЭС используются более интенсивно.
, т.к. ресурсы в первой ИЭС используются более интенсивно.
Математическая модель обоснования инновационно-инвестиционного процесса
Пусть (2) – некоторая ПФ. Очевидно, в зависимости от управления, освоение dxi , i=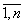 , может идти по-разному. В общем случае коэффициент освоения
, может идти по-разному. В общем случае коэффициент освоения
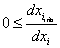 , i=
, i=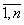 – для каждого из дифференциалов.
– для каждого из дифференциалов.
Понятно, что высокий коэффициент освоения ещё не гарантирует целесообразность инновационно-инвестиционного процесса. Актуальным является вопрос о цене освоения вектора {dxi}, i=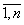 . Возникает острая необходимость введения качественной характеристики процесса, оценки управления, что в свою очередь предполагает определенную эластичность замещения факторов xi, i=
. Возникает острая необходимость введения качественной характеристики процесса, оценки управления, что в свою очередь предполагает определенную эластичность замещения факторов xi, i=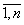 . Заметим, что факторы xi= xi(t), i=
. Заметим, что факторы xi= xi(t), i=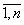 (t - время) являются, как правило, непрерывными функциями по t и для tÎ[t0,ti] определяют некоторую область G. Тогда управление (способ освоения {xi dxi} i=
(t - время) являются, как правило, непрерывными функциями по t и для tÎ[t0,ti] определяют некоторую область G. Тогда управление (способ освоения {xi dxi} i=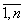 ) можно представить траекторией в некотором фазовом пространстве с обобщенными координатами xi, i=
) можно представить траекторией в некотором фазовом пространстве с обобщенными координатами xi, i=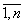 . Отметим, что функция (1) не имеет не только абсолютного максимума, но и локальных экстремумов. Поэтому самое лучшее, на что можно рассчитывать, если руководствоваться величиной индекса Y, выбирая ту или иную траекторию управления в области G, – это получить наибольшее ΔY при минимальных затратах {xi dxi} i=
. Отметим, что функция (1) не имеет не только абсолютного максимума, но и локальных экстремумов. Поэтому самое лучшее, на что можно рассчитывать, если руководствоваться величиной индекса Y, выбирая ту или иную траекторию управления в области G, – это получить наибольшее ΔY при минимальных затратах {xi dxi} i=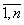 . Если обозначить через r некоторый показатель качества управления, то можно заметить, что xi , dxi, ΔY, r – мультиколлинеарны и едва ли есть практический смысл в выяснении характера этих зависимостей в данной работе, хотя само по себе качество управления r должно учитывать взаимозависимость всех факторов.
. Если обозначить через r некоторый показатель качества управления, то можно заметить, что xi , dxi, ΔY, r – мультиколлинеарны и едва ли есть практический смысл в выяснении характера этих зависимостей в данной работе, хотя само по себе качество управления r должно учитывать взаимозависимость всех факторов.
Не будем рассматривать такие важные вопросы, как расчет предельной производительности труда, учет роста нейтрального технического прогресса, материального прогресса и т.д. Считаем, что все как перечисленные, так и не указанные факторы, вносят свой вклад в самый обобщенный показатель функционирования системы, а именно определяют положение кривой управления в области G, что в свою очередь определит «отстояние» её от некоторой фиксированной траектории 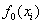 , i=
, i=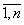 .
.
Если достаточно обоснованно выбрать 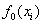 , то «отстояние» от неё f(xi)=0 , i=
, то «отстояние» от неё f(xi)=0 , i=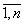 соответствующей реальному «потреблению» ресурсов xi , i=
соответствующей реальному «потреблению» ресурсов xi , i=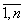 можно рассматривать как оценку управления с позиции получений Ymax. Понятно, что вопрос должен быть рассмотрен в гильбертовом пространстве, где эта оценка получится естественно при задании соответствующей метрики.
можно рассматривать как оценку управления с позиции получений Ymax. Понятно, что вопрос должен быть рассмотрен в гильбертовом пространстве, где эта оценка получится естественно при задании соответствующей метрики.
Рассмотрим подробнее вопросы оценки целесообразности инновационно-инвестиционного процесса с точки зрения максимизации результата – индекса Y. Как видно на рис. 3, из точки А, характеризуемой 1Y, объем работ 2У может быть достигнут на конкретной ИЭС, для которой рассчитана ПФ, бесконечным множеством сочетаний труда и прочих ресурсов, например, В, С и D. В зависимости от возможностей ИЭС, условий её работы, цели и задач выбирается тот или иной вариант использования ресурсов.
Оптимальную траекторию, ведущую из точки (xi,0), i=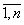 , определим как линию, касательные к которой в каждой точке совпадают с вектором ÑY, т.е. обобщенные координаты векторов
, определим как линию, касательные к которой в каждой точке совпадают с вектором ÑY, т.е. обобщенные координаты векторов
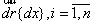 и
и 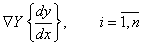
должны быть пропорциональны.
Линеаризуя (1) получим:
z=lgC0 +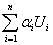 , где z=lgy,
, где z=lgy,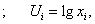 i=
i=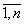 .
.
Выбирая соответствующие постоянные интегрирования, получим для оптимальной траектории:
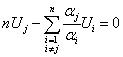 ,
,
где 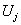 – один из производственных факторов или в «реальных» факторах:
– один из производственных факторов или в «реальных» факторах:
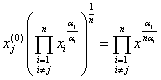 . (3)
. (3)
Заметим, что xj(0) есть функция аргумента t (время).
Пусть реальное управление (освоение производственных факторов) задано уравнением xjº xj(t) (ясно, что все xi , i=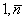 связаны через параметр t).
связаны через параметр t).
Тогда качество управления естественно рассматривать как меру отклонения xj от xj(0) в пространстве L2(t0;t1), т.е. ввести r – следующим образом:
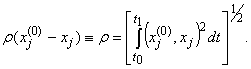 (4)
(4)
Исходя из экономического смысла xj(0) и xj непрерывности функции
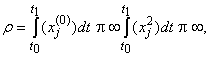
т. е. функция (xj(0) – xj ) – интегрируема, в конечном смысле на отрезке [t0;t1]. Аксиомы метрики, заданной формулой (3), выполняются очевидным образом:
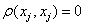
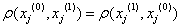
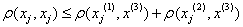
Следовательно, пространство управлений является метрическим с метрикой (4). Учитывая экономический смысл метрики, величину 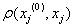 принимаем за характеристику качества управления xj. Как указано ранее, инновационно-инвестиционный процесс рассматривается как воздействие, изменяющее {xi} i=
принимаем за характеристику качества управления xj. Как указано ранее, инновационно-инвестиционный процесс рассматривается как воздействие, изменяющее {xi} i=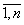 на {dxi} i=
на {dxi} i=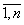 т.е. как появление в системе вектора {xi + dxi} i=
т.е. как появление в системе вектора {xi + dxi} i=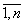 . теоретический максимальный отклик Y0 на вектор {dxi} i=
. теоретический максимальный отклик Y0 на вектор {dxi} i=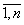 определяется из (1) с учетом соотношения:
определяется из (1) с учетом соотношения:
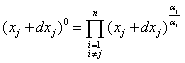 (5)
(5)
Естественно предположить, что в действительности отклик YR будет отличаться от Y0 и притом тем больше, чем больше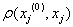 .
.
YR можно с достаточной точностью аппроксимировать функцией:
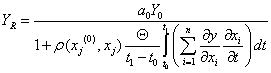 , (6)
, (6)
где 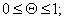
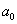 - множитель, определяющий необходимую размерность правой части формулы.
- множитель, определяющий необходимую размерность правой части формулы.
Заметим, что 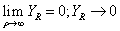 и при
и при
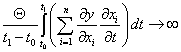
Пусть S(dx), i=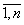 - затраты процесса.
- затраты процесса.
Y*=Y(xi*), i=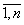 - расчетный индекс результата инновационно-инвестиционного процесса.
- расчетный индекс результата инновационно-инвестиционного процесса.
Тогда, очевидно, процесс будет оправданным лишь при выполнении условия:
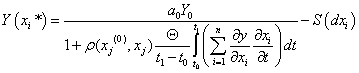 , (7)
, (7)
Так как проверка условия (7) при известной ПФ осуществляется до начала процесса, то появляется возможность оценить заранее целесообразность проектируемого вмешательства в ИЭС, а также наметить пути увеличения YR за счет уменьшения 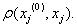
Обоснование четырехмерной модели управления инновационно-инвестиционным процессом с помощью квазипреобразования Лоренца
По Минковскому положение события задаётся четырьмя координатами — тремя пространственными и одной временнóй [15]. Обычно используются координаты: 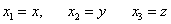 , где х, у, z – прямоугольные декартовы координаты события в некоторой инерциальной системе отсчёта (ИСО) и x°=ct, где t – время события, с – скорость света в вакууме. Геометрические свойства четырехмерного пространства определяются выражением для квадрата расстояния между двумя событиями (интервала)
, где х, у, z – прямоугольные декартовы координаты события в некоторой инерциальной системе отсчёта (ИСО) и x°=ct, где t – время события, с – скорость света в вакууме. Геометрические свойства четырехмерного пространства определяются выражением для квадрата расстояния между двумя событиями (интервала)  :
:
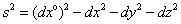 , (8)
, (8)
где 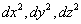 – разности координат событий, а
– разности координат событий, а 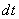 – разность их моментов времени. Пространство с таким
– разность их моментов времени. Пространство с таким 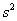 – псевдоевклидово.
– псевдоевклидово.
Для решения задачи управления в обобщенном четырехмерном пространстве выражение (8) может быть представлено как:
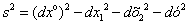 , (9)
, (9)
где 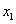 – труд;
– труд; 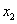 – фонды (основные и оборотные);
– фонды (основные и оборотные); 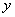 – например, объем ВРП. Тогда
– например, объем ВРП. Тогда 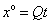 , где
, где 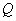 – условная максимальная производительность труда, q – производительность труда, характеризующая систему, в которой планируется инновационно-инвестиционный процесс.
– условная максимальная производительность труда, q – производительность труда, характеризующая систему, в которой планируется инновационно-инвестиционный процесс.
При переходе от одной инерциальной системы отсчета к другой пространственные координаты и время преобразуются друг через друга посредством квазипреобразования Лоренца. Известно, что система отсчёта называется инерциальной, если по отношению к ней любая свободная от взаимодействий с другими объектами (изолированная) материальная точка движется равномерно и прямолинейно. В специальной теории относительности преобразованию Лоренца подвергаются координаты (x, y, z, t) каждого события при переходе от одной ИСО к другой. Аналогично преобразуются координаты любогочетвертого вектора [13].
Преобразования Лоренца – это преобразования, сохраняющие неизменной метрику Минковского. Это значит, что последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой. Преобразования Лоренца – это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса (базис, составленный из попарно ортогональных векторов) к другому или обобщением понятия движения в евклидовом пространстве. Общая группа преобразования состоит из комбинаций пространственных отображений во времени и преобразований, которые с физической точки зрения являются преобразованиями перехода от одной инерциальной системы отсчета к другой [13]. Преобразования в плоскости с псевдоевклидовой метрикой является специфической чертой преобразования, что чрезвычайно важно для нашего исследования.
Преобразования в процессе управления осуществляются при коллинеарных пространственных осях, если инерциальная система отсчета 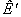 движется относительно инерциальной системы отсчета К с постоянной скоростью (рис. 1). В нашей задаче под скоростью мы понимаем производительность труда – q, характерной для инерциальной системы отсчета, в которой планируется инновационно-инвестиционный процесс и
движется относительно инерциальной системы отсчета К с постоянной скоростью (рис. 1). В нашей задаче под скоростью мы понимаем производительность труда – q, характерной для инерциальной системы отсчета, в которой планируется инновационно-инвестиционный процесс и 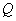 – максимальная производительность труда, принятая в качестве эталона, характерная для наиболее прогрессивной ИЭС. Начала координат совпадают в начальный момент времени в обеих системах [13]. Тогда прямые квазипреобразования Лоренца для решения задачи управления в трехмерном пространстве и времени получат вид:
– максимальная производительность труда, принятая в качестве эталона, характерная для наиболее прогрессивной ИЭС. Начала координат совпадают в начальный момент времени в обеих системах [13]. Тогда прямые квазипреобразования Лоренца для решения задачи управления в трехмерном пространстве и времени получат вид:
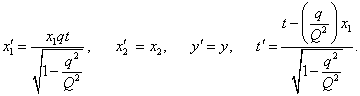 (10)
(10)
Рассмотрим графическую модель (рис.2) двухфакторной ПФ в трехмерном пространстве. Допустим, вся совокупность возможных сочетаний ресурсов, результатов работ и управлений, формализованных поверхностью 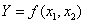 перемещается во времени, куда идут мировые линии материальных объектов, образуя какую-то гиперповерхность. Тогда оптимальное управление, характеризуемое вектором
перемещается во времени, куда идут мировые линии материальных объектов, образуя какую-то гиперповерхность. Тогда оптимальное управление, характеризуемое вектором 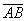 , условно перемещаясь, образует плоскость
, условно перемещаясь, образует плоскость  , которая характеризует процесс управления во времени (рис. 3).
, которая характеризует процесс управления во времени (рис. 3).
Для практических целей, допускаем относительную стабильность параметров производственной функции 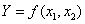 во времени [8]. На основании исследований установлено, что для современного уровня развития производства период времени, влиянием которого в расчетах с помощью ПФ можно пренебречь, в данной модели принимается равным одному году[10]. Изменения претерпевают параметры ресурсов и объемов работ во времени, зависящие от управления. Задача состоит в том, чтобы показать, как, реализуется управление при постоянно изменяющихся условиях выполнения работ, развивающихся во времени.
во времени [8]. На основании исследований установлено, что для современного уровня развития производства период времени, влиянием которого в расчетах с помощью ПФ можно пренебречь, в данной модели принимается равным одному году[10]. Изменения претерпевают параметры ресурсов и объемов работ во времени, зависящие от управления. Задача состоит в том, чтобы показать, как, реализуется управление при постоянно изменяющихся условиях выполнения работ, развивающихся во времени.
Практическая реализация модели визуализации управления в трехмерном пространстве и времени
Рассмотрим два частных варианта модели управления. Первый – идеальный. Рассмотрим перемещение вектора управления во времени в пределах заданных параметров. Преобразования при коллинеарных пространственных осях осуществляется при перемещении с определенной скоростью (производительность труда - q), аначала координатсовпадают в начальный момент времени в обеих системах. В результате перемещения без пространственных поворотов в заданной системе объекта
во времени в пределах заданных параметров. Преобразования при коллинеарных пространственных осях осуществляется при перемещении с определенной скоростью (производительность труда - q), аначала координатсовпадают в начальный момент времени в обеих системах. В результате перемещения без пространственных поворотов в заданной системе объекта 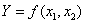 образуются гиперповерхность и плоскость
образуются гиперповерхность и плоскость  . Тогда длина отрезка
. Тогда длина отрезка
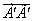 , характеризующая проекцию вектора оптимального управления во времени, будет равна длине вектора характеризующего оптимальное управление
, характеризующая проекцию вектора оптимального управления во времени, будет равна длине вектора характеризующего оптимальное управление 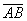 в соответствии с принятым критерием оптимальности.
в соответствии с принятым критерием оптимальности.
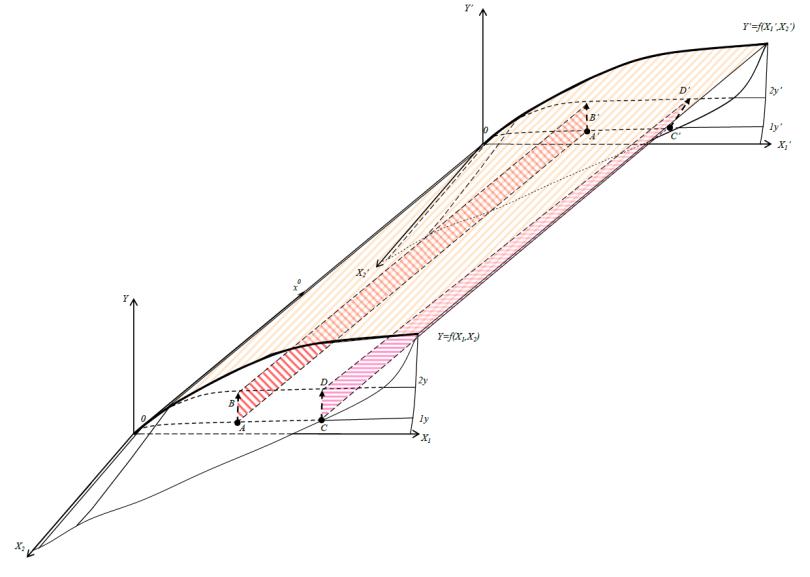
Рис. 3. Пространственная эконометрическая модель в п.-в., иллюстрирующая временные сечения пространства Минковского для векторов управления 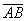 и
и 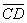 (преобразования
(преобразования 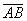 в
в 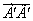 и
и 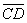 в
в 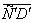 )
)
Второй вариант. Внесем незначительное изменение в идеальную модель. Известно, что в силу влияния различных внешних и внутренних причин в реальных условиях, в управляемой и управляющей системах допускаются отклонения в параметрах управления. Тогда, например, вектор 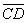 , под влиянием этих причин получит отклонение и, перемещаясь в пространстве производственных отношений и во времени, преобразуется в вектор
, под влиянием этих причин получит отклонение и, перемещаясь в пространстве производственных отношений и во времени, преобразуется в вектор 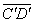 . Параметры вектора управления
. Параметры вектора управления 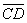 , построенного по указанному выше критерию оптимальности, получат искажение и его вид может быть представлен, например, как
, построенного по указанному выше критерию оптимальности, получат искажение и его вид может быть представлен, например, как 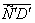 . Положение
. Положение 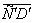 не перпендикулярно
не перпендикулярно 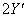 и, следовательно,
и, следовательно, 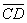 ¹
¹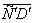 и положение
и положение 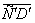 не соответствует принятому критерию оптимальности.
не соответствует принятому критерию оптимальности.
Допустим, в реальных условиях управление в пространстве начинается от точки А (от достигнутого результата) в направлении точки В (планируемого результата). Фактическое развитие процесса завершается с течением времени от 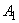 к
к 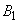 . В зависимости от процессов, связанных с управлением, развивающихся во времени, точка В вектора
. В зависимости от процессов, связанных с управлением, развивающихся во времени, точка В вектора 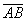 описывает достаточно сложную траекторию (рис.4). В силу совокупности факторов, влияющих на выполнение работ, не учтенных проектом, изменяющихся условий, запаздывания в реакции управляющей системы на изменения в процессе производства, в том числе и перерегулирование [6], и других причин траекторию перемещения вектора управления во времени в общем виде можно представить, например, рядом последовательных кривых (Рис. 4).
описывает достаточно сложную траекторию (рис.4). В силу совокупности факторов, влияющих на выполнение работ, не учтенных проектом, изменяющихся условий, запаздывания в реакции управляющей системы на изменения в процессе производства, в том числе и перерегулирование [6], и других причин траекторию перемещения вектора управления во времени в общем виде можно представить, например, рядом последовательных кривых (Рис. 4).
Например, вектор 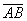 под влиянием реальных условий, и реакции управляющей системы для компенсации отклонений от заданных параметров совершает колебания во времени относительно заданного направления. Несмотря на эти процессы управляемой системе, удалось выйти на уровень 2Y в точке
под влиянием реальных условий, и реакции управляющей системы для компенсации отклонений от заданных параметров совершает колебания во времени относительно заданного направления. Несмотря на эти процессы управляемой системе, удалось выйти на уровень 2Y в точке 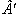 и
и 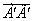 =
=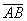 .
.
Рассуждая аналогично, по отношению 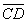 (рис 4), показано, что управляющая система не обеспечила решение задачи управления, связанной с выходом на 2Y по кратчайшему расстоянию в соответствии с принятым нами критерием оптимальности (См. также рис. 3), что характеризует качество управления.
(рис 4), показано, что управляющая система не обеспечила решение задачи управления, связанной с выходом на 2Y по кратчайшему расстоянию в соответствии с принятым нами критерием оптимальности (См. также рис. 3), что характеризует качество управления.
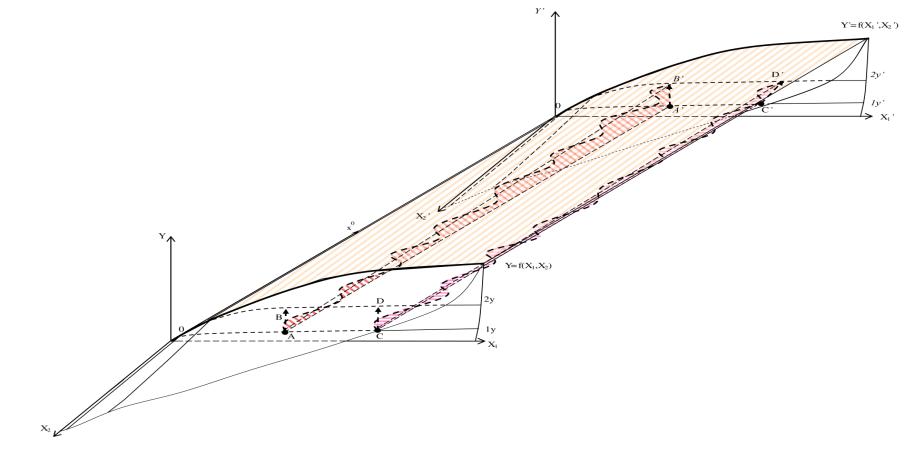
Рис.4. Пространственная эконометрическая модель, иллюстрирующая временные сечения пространства Минковского для векторов управления 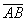 и
и 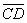 (преобразования
(преобразования 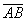 в
в 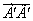 и
и 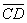 в
в 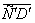 ) с учетом реакции векторов управления на влияние внешних и внутренних факторов в ИЭС.
) с учетом реакции векторов управления на влияние внешних и внутренних факторов в ИЭС.
Следует отметить, что весьма сложная поверхность, образованная перемещением вектора 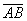 или
или 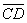 во времени (рис.4), также является количественной характеристикой экономического процесса. В частности, как мы условились в (10), в нашей задаче под скоростью понимается производительность труда – q, характерная для ИЭС. Тогда площадь поверхности, образованная при перемещении вектора во времени
во времени (рис.4), также является количественной характеристикой экономического процесса. В частности, как мы условились в (10), в нашей задаче под скоростью понимается производительность труда – q, характерная для ИЭС. Тогда площадь поверхности, образованная при перемещении вектора во времени 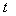 характеризует затраты на реализацию проекта. Чем меньше площадь, тем эффективнее инновационно-инвестиционный процесс.
характеризует затраты на реализацию проекта. Чем меньше площадь, тем эффективнее инновационно-инвестиционный процесс.
Моделирование управления инновационно-инвестиционных процессов в пространстве открывает возможности для более полного экономического анализа, исследования пространственныхструктур, не только объектов, но и процессов, протекающих в ИЭС,отражает важнейшие сведения о свойствах реальных экономических процессов.
ЗАКЛЮЧЕНИЕ
Методология развития пространственной экономики создает предпосылки для разработки моделей управления интегрированными экономическими системами, которые способны обеспечить приращение качества экономического анализа. Основой пространственного моделирования управления инновационно-инвестиционным процессом является ПФ, прежде всего, как инструмент оценки эффективности использования ресурсов. Алгебраическое введение дифференциалов ресурсов в ПФ интегрированной экономической системы позволяет визуализировать инновационно-инвестиционный процесс и прогнозировать эффективные варианты его реализации. Квазипреобразование Лоренца и обобщенное пространство Минковского позволяют визуализировать управление инновационно-инвестиционным процессом в четырехмерном пространстве, объединяющим физическое трёхмерное пространство ресурсов ивремя. Наглядное представление управления в пространстве 4D играет важную роль не только как обладающее большой познавательной и доказательной силой, но и как инструмент, способствующий лучшему пониманию экономических процессов, в оценке и поиске оптимального управления.
СПИСОК ЛИТЕРАТУРЫ
1. Боровик В.С. Модель управления внедрением новой технологии на основе производственной функции / В.С.Боровик, В.В.Боровик, Ю.Е.Прокопенко // Экономический анализ: теория и практика. - 2013. -№ 42 (345). – С.25-30.
2. Боровик В. С. Моделирование управления в социально-экономических системах с учетом человеческого фактора на основе теории подобия / В. С. Боровик, Е.Ю.Зайцева // Известия ВолгГТУ: Актуальные проблемы управления, вычислительной техники и информатики в технических системах. Волгоградский государственный технический университет. – Волгоград, 2012. –Вып. 15 (102)– С. 8–12.
3. Гранберг А.Г. Основы региональной экономики. М.: ГУ -ВШЭ, 2003. 495 с.
4. Казарян В. П. Понятие времени в структуре научного знания [Текст] / В. П. Казарян. – М.: Изд-во МГУ, 1980. – 225 с.
5. Минакир П.А. Экономический анализ и измерения в пространстве // Пространственная экономика. 2014. №1. С.12-39.
6. Михайлов В. С.Теория управления [Текст] / В. С. Михайлов.— Киев: Выща школа. Головное издательство, 1988.— 312 с.
7. Полтерович В.М. Гипотеза об инновационной паузе и стратегии модернизации // Вопросы экономики. 2009. №6. С 12.
8. Терехов Л. Л. Производственные функции. Статистика [Текст] / Л. Л. Терехов. – М., 1974. – 127 с.
9. Фащевский А. Б. Графическое изображение четырехмерного пространства [Электронный ресурс] / А. Б. Фащевский. – Режим доступа http://khd2.narod.ru/authors/fshvsky/spc4d.htm. – Дата обращения 30.12.14. 10. Харитонов В. В. Аналитическая модель эффективности инвестиционных проектов в энергетике [Текст] / В. В. Харитонов, Н. А. Молоканов // Экономический анализ: теория и практика. – 2013. – № 16 (319). – C. 19.11. Шумпетер Й. История экономического анализа. В трех томах. Спб.: -Экономическая школа, 2004.
12. Ярмолинский В. А. Повышение эффективности использования производственных ресурсов в условиях неопределенности финансирования дорожных объектов [Текст] / В. А. Ярмолинский, А. М. Хакимов // Вести Тихоокеанского государственного университета. – 2011. – № 1. – C. 11–19.
13. Carmeli, Moshe. Group Theory and General Relativity, Representations of the Lorentz Group and Their Applications to the Gravitational Field / Moshe Carmeli. – McGraw-Hill, New York, 1977. – 311 p.
14. Cohn-Vossen, S. Anschauliche Geometri / S. Cohn-Vossen, D. Hilbert. – Berlin: Verlang von J. Springer, 1932. – 325 p.
15. Crevoisier O. The Innovative Milieus Approach: Toward a Territorialized
Understanding of the Economy? // Economic Geography. 2004. Vol. 80. . 4. P. 367—379.
16. Drucker, P. F. Entrepreneurschip and innovation / P. F. Drucker. – New York: Harper a. Row, IX, 1995. – 277 p.
17. Maillat D., Crevoisier O., Vasserot J.-Y. Innovation et district industriel: l’Arc jurassiensuisse // Maillat D., Perrin J.-C. (eds.) Entreprises innovatrices et developpement territorial.Neuchatel: GREMI/EDES, 1992. P. 105—125.
18. Minkowski, Hermann. Geometrie der Zahlen / Hermann Minkowski. – Leipzig-Berlin: R. G. Teubner, 1910. – 320 p.
19. Yukihito, Sakai. Four-dimensional Mathematical Data Visualization via “Embodied Four-dimensional Space Display System” Faculty 2 Research of Information Sciences and Arts, Toyo University, 2100 Kujirai, Kawagoe, Saitama [Electronic resource] / Sakai Yukihito, Shuji Hashimoto. – Available at: http://www.scipress.org/journals/forma/pdf/2601/26010011.pdf. – Last access 30.04.2014.
20. Whitrow, G. J. The Natural Philosophy / G. J. Whitrow. – Published December 3rd by Oxford University Press, 1981. – 410 р.
RЕFERENCES
1. Borovik V.S. Management Model introduction of new technology based on the production function / V.S.Borovik, V.V.Borovik, Yu.E.Prokopenko / / Economic Analysis: Theory and Practice. - 2013. - № 42 (345). - P.25-30. (In Russian).
2. Borovik, V.S. Simulation Control in the socio-economic systems, taking into account the human factor on the basis of similarity theory / V. Borovik, E.Yu.Zaytseva / / News VSTU: Actual problems of management, computer science and informatics in technical systems. Volgograd State Technical University. - Volgograd, 2012., Vol. 15 (102) - Р. 8-12. (In Russian).
3. Granberg A.G. Fundamentals of the regional economy. M.: HSE, 2003. -495 p. (In Russian).
4. Kazarian, V.P. notion of time in the structure of scientific knowledge / VP Kazarian. - Moscow: MGU, 1980. – 225p. (In Russian).
5. Minakir, P.A. Economic analysis and measurement in the space / / Spatial Economics. 2014. № 1. P.12-39. (In Russian).
6. Mikhailov, V.S. Control Theory / V.S. Mikhailov. - Kiev: Vyshcha school. Head Publishing, 1988. – 312p. (In Russian).
7. Polterovich V. Innovation pause hypothesis and modernization strategy / / Problems of Economics. 2009. № 6. P. 4-23. (In Russian).
8. Terekhov, L.L. Production functions. Statistics / L.L. Terekhov. - M., 1974. – 127p. (In Russian).
9. Faschevsky, A.B. Graphic representation of four-dimensional space [electronic resource] / A.B. Faschevsky. - Mode of access http://khd2.narod.ru/authors/fshvsky/spc4d.htm. - Access Date 12/30/14. (In Russian).
10. Kharitonov, V.V. Analytical model of efficiency of investment projects in energy / V. Kharitonov, N.A. Molokanov / / Economic Analysis: Theory and Practice. - 2013. - № 16 (319). - P. 19. (In Russian).
11. J. Schumpeter, History of Economic Analysis. In three volumes. SPB.:-The School of Economics, 2004. (In Russian).
12. Yarmolinsky, V.A. Improved utilization of productive resources in the face of uncertainty of funding road projects / V.A. Yarmolinsky, A.M. Khakimov / / News Pacific State University. - 2011. - № 1. - P. 11-19. (In Russian).
13. Carmeli, Moshe. Group Theory and General Relativity, Representations of the Lorentz Group and Their Applications to the Gravitational Field / Moshe Carmeli. – McGraw-Hill, New York, 1977. – 311 p.
14. Cohn-Vossen, S. Anschauliche Geometri / S. Cohn-Vossen, D. Hilbert. – Berlin: Verlang von J. Springer, 1932. – 325 p.
15. Crevoisier O. The Innovative Milieus Approach: Toward a Territorialized
Understanding of the Economy? // Economic Geography. 2004. Vol. 80. . 4. P. 367—379.
16. Drucker, P. F. Entrepreneurschip and innovation / P. F. Drucker. – New York: Harper a. Row, IX, 1995. – 277 p.
17. Maillat D., Crevoisier O., Vasserot J.-Y. Innovation et district industriel: l’Arc jurassiensuisse // Maillat D., Perrin J.-C. (eds.) Entreprises innovatrices et developpement territorial.Neuchatel: GREMI/EDES, 1992. P. 105—125.
18. Minkowski, Hermann. Geometrie der Zahlen / Hermann Minkowski. – Leipzig-Berlin: R. G. Teubner, 1910. – 320 p.
19. Yukihito, Sakai. Four-dimensional Mathematical Data Visualization via “Embodied Four-dimensional Space Display System” Faculty 2 Research of Information Sciences and Arts, Toyo University, 2100 Kujirai, Kawagoe, Saitama [Electronic resource] / Sakai Yukihito, Shuji Hashimoto. – Available at: http://www.scipress.org/journals/forma/pdf/2601/26010011.pdf. – Last access 30.04.2014.
20. Whitrow, G. J. The Natural Philosophy [Text] / G. J. Whitrow. – Published December 3rd by Oxford University Press, 1981. – 410 р.
Боровик Виталий Сергеевич
доктор технических наук, профессор, заведующий кафедрой
Кафедра экономики и управления дорожным хозяйством
Волгоградский государственный архитектурно-строительный университет
Академическая, 1, Волгоград, Россия, 400074
Сведения о наличии печатных произведений в общегосударственных и международных базах данных: 86
Контактный телефон: 89023630079
Номер ORCID 0000-0002-8845-9339
borovikv@mail.ru
Боровик Виталий Витальевич
Кандидат технически наук, доцент кафедры строительства транспортных сооружений
Волгоградский государственный архитектурно-строительный университет
Академическая, 1, Волгоград, Россия. 400074
Сведения о наличии печатных произведений в общегосударственных и международных базах данных: 18
Контактный телефон: 89047730007
Номер ORCID 0000-0002-2409-4078.
borovikvv70@mail.ru
Borovik Vitaly Doctor of Technical Sciences, Professor, Head of Department of Economics and road management Chair Volgograd State University of Architecture and Civil Engineering Academic, 1, Volgograd, Russia, 400074 Information about the availability of printed works in national and international databases: 86 Telephone: 89023630079 Phone ORCID 0000-0002-8845-9339 borovikv@mail.ru
Vitaly V. Borovik Ph.D., assistant professor of construction of transport facilities Ph.D., Associate Professor (full) Volgograd State University of Architecture and Civil Engineering Academic, 1, Volgograd, Russia. 400074 Information about the availability of printed works in national and international databases: 18 Telephone: 89047730007 Phone ORCID 0000-0002-2409-4078. borovikvv70@mail.ru
[1] На эти свойства ПФ указывал Й. Шумпетер, отмечая, что «…диаграмма с двумя факторами является, возможно, самым лучшим средством демонстрации (выделено авторами.) на элементарном уровне того, как ресурсы, взаимодействующие в производстве, могут в определенных пределах «конкурировать» друг с другом и как два эффекта соотносятся в случае двух взаимозаменяемых факторов». [11, стр. 1373]
[2] Представляет также интерес замечание Й. Шумпетера относительно введения в ПФ параметра времени: «Если мы хотим основать свою теорию производства на теории «окольного» процесса Джевонса - Бём-Баверка - Тауссига, мы можем ввести время непосредственно в производственную функцию, записав: 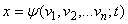 к этому шагу подводит трактовка Викселем проблем капитала, и этот шаг был сделан многими современными авторами…». [11, стр. 1353]
к этому шагу подводит трактовка Викселем проблем капитала, и этот шаг был сделан многими современными авторами…». [11, стр. 1353]
[3] Математическая энциклопедия. Т 4. Издательство Советская энциклопедия. М., 1984. Стр. 719.
4 Математическая энциклопедия. Т 4. Издательство Советская энциклопедия. М., 1984. Стр. 148.
[5] Фащевский А.Б предложил развитие схемы [9].
[6] Математическая энциклопедия. Т 1. Издательство Советская энциклопедия. М., 1984. Стр. 843.
[7] Эйнштейн «Сущность теории относительности» Электронный ресурс. Код доступа http://murzim.ru/jenciklopedii/100-velikih-knig/4190-eynshteyn-suschnost-teorii-otnositelnosti.html. Дата обращения 20.08.2014.
[8]А. Эйнштейн пришел к выводу, что принцип относительности является всеобщим. На основании постулата, что все законы природы одинаковы во всех инерциальных системах отсчета, он установил, что не только механические, но и все физические законы одинаковы во всех инерциальных системах отсчета. Эйнштейн А.Основные идеи и проблемы теории относительности // Собрание научных трудов, т. II. — М., 1966. — стр. 120
[10] Бессонов В.А. Проблемы построения производственных функций в российской переходной экономике. Стр. 39, 73. [Электронный ресурс] / В.А.Бессонов / -Режим доступа-
http://www.economicus.ru/macroeconomica/readings/Prois_funk.pdf - Дата обращения 11.04.2014.
