Потенциалы субъектов хозяйствования

Целью настоящего исследования является изучение с привлечением элементов математической экономики содержания понятий экономического и производственного потенциалов субъектов хозяйствования на примере промышленных предприятий, особенностей, сходства и различий между ними и проведение аналогии между экономическим потенциалом предприятий и потребительским потенциалом субъектов жизнедеятельности с позиций развиваемой автором на основе концепции потенциала в экономике как определенной способности экономических субъектов общей экономической теории потенциалов [5, 6, 7, 8, 9, 10].

Фундамент этой теории образуют следующие положения.

Носителями потенциалов в экономике являются экономические субъекты.

Потенциал произвольного субъекта экономики – это способность данного субъекта к осуществлению имманентно присущей ему деятельности, характеризующей максимально возможный результат такой деятельности.

Видовое разнообразие потенциалов, в связи с этим, порождается, прежде всего, типологией субъектов экономики и видов деятельности, а в основе систематизации потенциалов должны лежать общепринятые классификации субъектов экономики и видов деятельности.

Непосредственное измерение уровня потенциалов, относящихся к классу латентных признаков экономических субъектов, невозможно, что обусловливает необходимость применения косвенных методов измерений.

Природе потенциалов как объектов измерения в наибольшей степени соответствует системное моделирование и экономико-математический анализ как инструменты оценки потенциалов.

Рассмотрим с этих позиций экономико-математическую интерпретацию экономического и производственного потенциалов предприятий и их аналогов в теории потребления.

В простейшем случае математическая модель производителя задается с помощью задачи оптимизации следующего вида [12]:

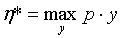(1)

при условии

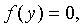(2)

где p – вектор цен; y – вектор чистого выпуска; h* – максимальная прибыль предприятия; f – производственная функция.

Поскольку оптимальное решение указанной задачи зависит от параметров, задаваемых извне (в рассматриваемом случае это вектор цен p – единственные параметры внешней среды, учитываемые в данной модели производителя), то максимальная прибыль h* является скалярной функцией цен

h* =h (p),

а оптимальный чистый выпуск y* – вектор-функцией цен

y* = n (p).

В математической экономике функция n называется функцией предложения.

В рамках развиваемой автором настоящего исследования концепции потенциалов, как легко видеть из отмеченного выше, функция h характеризует экономический потенциал производителя, т.е. представляет собой потенциальную функцию, отражающая зависимость максимально возможной чистой прибыли (основного конечного результата любой хозяйственной деятельности предприятий) от параметров состояния предприятия и параметров внешней среды (в рассматриваемом случае ценовой конъюнктуры рынка производственных ресурсов и конечной продукции).

Функция n, в отличие от функции h, отражает оптимальные (с точки зрения целевой функции и условий задачи (1)-(2)), но не предельно возможные для предприятия, объемы чистого выпуска. Указанные объемы выпуска для данного предприятия являются лишь экономически целесообразными, обусловленными как технологическими (производственными) возможностями предприятия, так и конъюнктурой рынка. Кроме того, выпущенная (реализованная) продукция не является конечным целевым результатом хозяйственной деятельности предприятий, а представляет собой лишь средство достижения главной цели – получение чистого дохода (приращение капитала и т.п.). Поэтому относить функцию n к классу потенциальных функций, характеризующих, в частности, экономический либо производственный (как наиболее близкий по содержанию функции n) потенциал неправомерно.

В самом деле, экономический потенциал предприятия отражает его способность генерировать чистый доход с учетом всей совокупности эндогенных для предприятия и экзогенных факторов. С этой задачей, в рамках предположений модели (1)-(2) в полном объеме справляется функция h.

Производственный потенциал, в соответствии с принятым автором определением потенциалов в экономике, должен отражать максимально возможный результат производственной деятельности предприятия, т.е. характеризовать обусловленные исключительно производственными факторами максимально возможные объемы производства продукции. Как было показано выше, функция предложения n эту задачу в чистом виде не решает, так как помимо производственных отражает действие и внешних конъюнктурных факторов.

Приведенному выше толкованию производственного потенциала в терминах модели предприятия (1)-(2) полностью соответствует понятие производственной функции (см, [1, 12]), характеризующей, в случае многономенклатурного производства, предельные в смысле оптимальности по Парето производственные возможности предприятия, его максимально возможные (технологически эффективные [12]) объемы выпуска продукции.

Таким образом, потенциальными функциями, характеризующими производственный потенциал предприятий, могут выступать производственные функции. Поскольку производственные ограничения в модели предприятия (1)-(2) задаются с помощью производственной функции f, функции вида n представляют собой некоторое обобщение и производственных функций. Однако, это обстоятельство, тем не менее, не позволяет их квалифицировать как потенциальные в силу указанных выше причин. (Этот вопрос в более общей постановке рассмотрен автором в статье [11].)

В математической теории потребления индивид (домашнее хозяйство) рассматривается как субъект экономики, основное предназначение которого состоит в удовлетворении собственных потребностей. Тем самым процесс жизнедеятельности индивида в простейших моделях ограничивается рассмотрением процесса потребления, цель которого заключается в удовлетворении потребителем своих потребностей.

Одним из основных постулатов теории потребления является принцип оптимальности поведения потребителя, в соответствии с которым потребитель способен из двух произвольных наборов благ выбрать тот из них, который обеспечивает максимальный уровень удовлетворения его потребностей. В простейшем случае это позволяет представить модель поведения потребителя в виде следующей оптимизационной задачи:

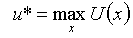(3)

при ограничениях вида

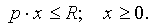(4)

Здесь U – функция полезности; x – набор потребленных благ; p – вектор цен; R – доход потребителя.

Как и в случае с аналогичной моделью производителя (модель (1)-(2)), равновесное поведение потребителя x* в различных внешних условиях при известной и заданной априори функции полезности U исчерпывающим образом описывается функцией спроса x

x* = x (p, R),

характеризующей зависимость равновесного набора благ x* от вектора цен на блага p и дохода потребителя R.

В экономико-математической теории потребления функция полезности считается заданной извне (имманентно присущей потребителю) и не является объектом экономических исследований. Отсутствуют и надежные теоретическое основания для количественного измерения и описания предпочтений потребителя и уровня удовлетворения его потребностей. Вероятно, отчасти и в силу этих причин основное внимание в теории потребления уделяется функции спроса x, а не косвенной функции полезности U’, т.е. функция вида

u* = U’ (p, R).

Вместе с тем именно косвенная функция полезности потребителя U’ в теории потребления является полным аналогом потенциальной функции h, выражающей экономический потенциал предприятия, и может выступать в качестве потенциальной функции, отражающей потребительский потенциал – потенциал потребителя.

Литература:

1. Вереникин А.О. Теория экономического потенциала и ее аналог в математической физике // Экономические проблемы инновационного развития : монография / Под ред. К.А.Хубиева. – М.: ТЕИС, 2009. – 699 с. – Режим доступа: http://verenikin.professorjournal.ru/c/document_library/get_file?uuid=1d97b05b-b784-452a-a53a-a16620801057&groupId=456709.

2. Карапейчик І.М. Кількісний аналіз потенційної функції підприємства з урахуванням комплексної дії ендогенних та екзогенних факторів / І.М. Карапейчик // Держава та регіони. – 2013. – № 4 (73). – С. 75-82.

3. Карапейчик И.Н. Классификации потенциалов в экономике: критический взгляд / И.Н. Карапейчик // Вісник Хмельницького національній університету. – 2012. – № 2, Т. 3, Економічні науки. – С. 116-125.

4. Карапейчик И.Н. Классификация потенциалов экономических субъектов: методологические аспекты и возможные решения / И.Н. Карапейчик // Актуальні проблеми економіки. – 2013. – № 1(139). – С. 20-31.

5. Карапейчик И.Н. Носители потенциалов в экономической теории / И.Н. Карапейчик // Ефективна економіка. – 2012. – № 8. – Режим доступа к журн.: http://www.economy.nayka.com.ua/index.php?operation=1&iid=1324.

6. Карапейчик И.Н. Обобщенный анализ потенциала предприятия как функции параметров внешней среды (теоретический подход) / И.Н. Карапейчик // Проблеми економіки. – 2013. – № 3. – С. 199-207.

7, Карапейчик И.Н. Оценка инновационного потенциала машиностроительных предприятий : монография / Карапейчик И.Н. – Мариуполь: "Новый мир", 2011. – 184 с.

8. Карапейчик И.Н. Понятие потенциала в экономике: задачи и направления исследований / И.Н. Карапейчик // Актуальні проблеми економіки. – 2012. – № 7 (133). – С. 16-25.

9. Карапейчик И.Н. Понятие потенциала в экономике: общая концепция / И.Н. Карапейчик // Ефективна економіка. – 2011. – № 12. – Режим доступа к журн.: http://www.economy.nayka.com.ua/index.php?operation=1&iid=820.

10. Карапейчик И.Н. Потенциальные функции и задача систематизации потенциалов в экономике / И.Н. Карапейчик // Інноваційні економіка. – 2012. – № 4(30). – С. 9-15.

11. Карапейчик І.М. Потенціали та інші граничні характеристики підприємств як об’єкт економічних досліджень / І.М. Карапейчик // Держава та регіони. – 2013. – № 1 (70). – С. 114-118.

12. Маленво Э. Лекции по микроэкономическому анализу / Маленво Э. – М.: Наука, 1985. – 390 с.