Применение теории игр в планировании деятельности промышленного кластера в условиях постоянного ассортимента

В теории игр стратегия игрока в игре или деловой ситуации— это полный план действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации. Многие исследователи рассматривают теорию игр не как инструмент предсказания поведения, но как инструмент анализа ситуаций с целью выявления наилучшего поведения для рационального игрока [1,2,4,6].

К точным методам решения игр в матричной форме относится метод Лагранжа и метод линейного программирования [6, 8]. Часто в практических задачах нет необходимости находить точное решение матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш, близкий к цене игры и приближённые оптимальные стратегии игроков. К итерационным (приближенным) методам относится метод Брауна-Робинсона [5, 8]. Он основан на многократном моделировании розыгрыша игры, что позволяет получить приближённое решение игры в смешанных стратегиях, т.е. вероятности выбора игроками каждой из возможных стратегий.

Рассмотрим возможность использования теории игр при оптимизации процесса перераспределения ассортимента продукции между предприятиями. В игре будут принимать участие 2 игрока: экономические субъекты и «природа». Термин «природа» в теории игр понимается в широком смысле. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и т.п. процессы, которые сопровождают экономическую деятельность. Под «природой» может также пониматься рынок, противостоящий предпринимателю, конкурирующая среда, монополия и т.п. «Природа» как часть экономики, не стремиться «специально» навредить предпринимателю, но она несёт определённый урон от его экономической деятельности.

Предполагаемую игру можно формализовать следующим образом.

Первый игрок как интегрированная структура ОАО «Воронежская Хлебная Компания» собирается проанализировать действия имеет 2-х экономических субъектов (имеет две стратегии):

А1 – ОАО «Тобус»,

А2 - ОАО «Хлебозавод №7».

В1 – объем производства, кг;

В2 – основное сырое, кг;

В3 - дополнительное сырое, кг;

В4 - накладные расходы, руб;

В5 - расходы на воду, руб;

В6 - расходы на упаковку, руб;

В8 – стоимость электроэнергии, руб;

В9 –прибыль, руб;

В10 – рентабельность, %.

Применим методы Лагранжа и Брауна-Робинсона к определению наиболее эффективной деятельности ОАО «Тобус» и ОАО «Хлебозавод №7». Для анализа используем типы продукции, выпускаемые на обоих предприятиях: хлеб «Дарницкий» подовый 0,67, хлеб «Украинский новый» формовой, «Батончик к чаю» 0,3, булка «Городская» 0,2, хлеб «Чиабатта» 0,35.

Расчетные характеристики относительно продукции хлеб Дарницкий подовый 0,67 приведены на рис. 1, 2. При расчете оптимальных стратегий использовалась программа Matrixgame [4].

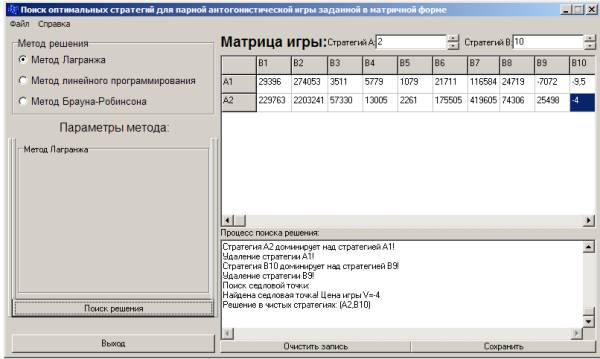
Рисунок 1 – Расчетные параметры методом Лагранжа

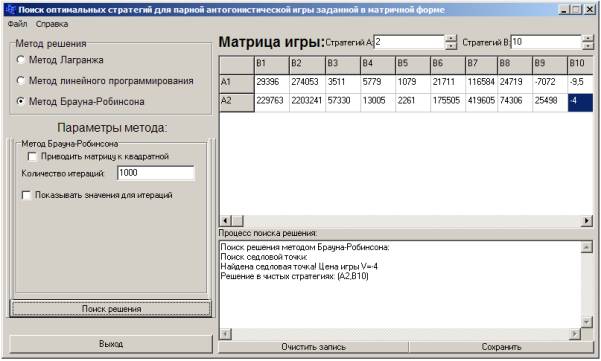
Рисунок 2 – Расчетные параметры методом Брауна-Робинсона

Оба метода дают одинаковый результат: хлеб «Дарницкий» подовый 0,67 выгоднее выпускать на Хлебозаводе № 7.

Однако расчетные характеристики для продукции «Батончик к чаю» 0,3 приведенные на рис. 3, 4, дает противоречивые характеристики. Метод Лагранжа с вероятностью 0,99 рекомендует выпуск изделия на ОАО «Тобус» (рис.3), а метод Брауна-Робинсона – на ОАО «Хлебозавод №7». В этом случае необходимо принимать решение с помощью экспертов, учитывая дополнительные, не учитываемые при данных расчетах, показатели.

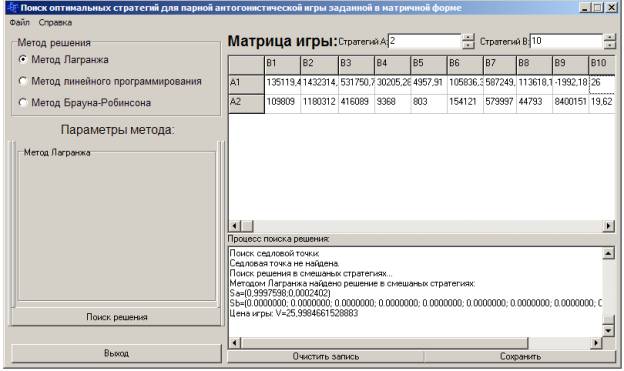
Рисунок 3 – Расчетные параметры для продукции батончик к чаю методом Лагранжа

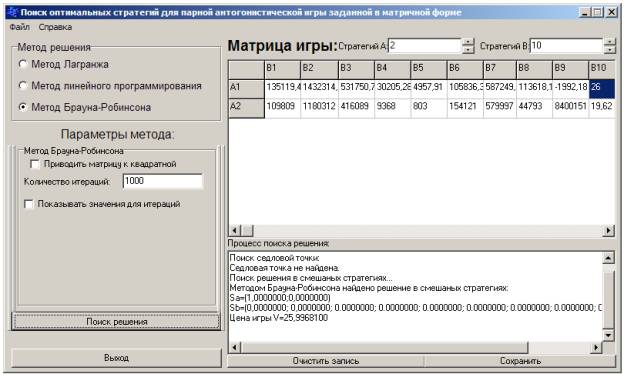
Рисунок 4 – Расчетные параметры для продукции батончик к чаю методом Брауна-Робинсона

Распределение остальных типов выпускаемой продукции по рассматриваемым предприятиям приведены в таблице 1.

Таблица 1 – Эффективность распределения производимой продукции по предприятиям

Наименование продукции	Тобус	Хлебозавод № 7
«Батончик к чаю» 0,3	Одинаковые приоритеты
Булка «Городская» 0,2	+	-
Хлеб «Дарницкий» подовый 0,67	-	+
Хлеб «Украинский новый» формовой	+	-
Хлеб «Чиабатта» 0,35	+	-

Таким образом, используя методы и модели теории игр, учитывающие статистическую информацию и основные показатели экономики производства, к каждому пункту выпускаемого ассортимента, можно построить оптимальную производственную стратегию предприятий.

Литература

1. Васин А.А., Морозов В.В. Введение в теорию игр с приложениями к экономике - Издательство: МГУ им. М.В. Ломоносова, 2003. – 277 с.

2. Воробьёв Н.Н. Матричные игры – М: Государственное Издательство Физико-Математической Литературы, 1961. - 282 с.

3. Гречкина П.В., Еремеев А.П. Программная система для решения антагонистических игр Matrixgame - [Электронный ресурс] URL: http://ctl.mpei.ru/pdfs/000516.pdf (дата обращения: 20.08.2014).

4. Дж. фон Нейман, Моргенштерн О. Теория игр и экономическое поведение. – М: Наука, 1970. – 708 с.

5. Итеративные методы в теории игр и программировании / Под общ. ред. В.З. Беленького, В.А. Волконского. - Сер. Экономико-математическая библиотека. - М. Наука, 1974. - 240с.

6. Мазалов В.В. Математическая теория игр и приложения - Санкт-Петербург - Москва - Краснодар: Лань, 2010. – 446 с.

7. Мулен Э. Кооперативное принятие решений – М: Мир, 1991. – 464 с.

8. Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр - СПб: БХВ-Петербург, 2012. - 432 с.