Колесник Ю.А.

Филиал ФГАОУ ВПО «Дальневосточный федеральный университет», г. Уссурийск

Моделирование конкуренции в среде малого бизнеса

Обычно,  конкуренция возникает в силу следующих причин; у одного или нескольких производителей появляется возможность лучше удовлетворить потребности потребителей; увеличить свое влияние на рынке, за счет лучшего качества продукции; оптимизировать свою деятельность и т.д. Как свидетельствует практика, самая острая конкуренция разворачивается обычно между теми производителями, которые предлагают сходную продукцию и услуги. И еще! Интенсивность конкуренции зависит от того, насколько активно участники рынка пытаются снизить цены на предлагаемую продукцию, или улучшить качество продукции, повысить уровень обслуживания потребителей и прочее. Иногда конкуренты прибегают к ассортиментной политике, когда на рынке предлагается не один вид продукции, а несколько, или стремятся усилить свои позиции за счет слабых сторон конкурентов.

Независимо от интенсивности конкурентной борьбы каждый участник игры вырабатывает свою стратегию поведения на рынке, которая бы способствовала его превосходство над конкурентами и укреплению по отношению к нему доверие покупателей. В тоже время, успех стратегии товаропроизводителя зависит от стратегий конкурентов и предлагаемой продукции конкурентами на обеспечение этих стратегий.

Существует огромное число факторов способствующих росту конкурентной борьбы. Мы назовем лишь некоторые.

1. Это-увеличение на рынке товаропроизводителей, некоторые из которых, способны предложить покупателям более привлекательную продукции;

2. Снижение спроса на продукцию;

3. Изменение цен, которые бы привели к росту объемов продаж продукции, а также иные приемы увеличения реализации товарной продукции продаж;

4. Попытки одной или нескольких товаропроизводителей улучшить свои позиции на рынке за счет других (менее значимых) конкурентов. Например, если некоторые товаропроизводители начинают испытывать трудности в реализации своей продукции, а, следовательно, теряют свои позиции на рынке, то для улучшения объемов продаж они, нередко активизируются: приобретают мелких конкурентов, внедряют новые виды продукции, снижают цены и пр. Такие действия приводят к переделу сфер влияния на рынке и обостряют конкуренцию.

Можно считать конкуренцию нежесткой («слабой»), если значительное количество товаропроизводителей удовлетворены темпами роста продаж и долями рынка, не практикуют переманивание (тем или иным способом) покупателей и получают неплохую прибыль. Особые отношения складываются между товаропроизводителями, когда на рынке могут появиться новые конкуренты. Не зная специфику ведения рыночных операций (цены, ассортимент продукции, сложившийся на рынке ранее и пр.) новички могут предложить покупателям новые виды продукции. Они же стараются занять свое место на рынке (обеспечить себе долю) и, имея значительные ресурсы, вступают в конкурентную борьбу. В целом, вероятность появления новых конкурентов зависит от ряда факторов. Это, наличие продукции, которая пользуется спросом у покупателей, ожидаемой реакции традиционных товаропроизводителей и не препятствование их принять новичка в свою среду. В практике рыночных отношений между товаропроизводителями бывают и такие случаи, что лучше отказаться новичку от планов вести торговлю в случае, если действующие там конкуренты могут перекрыть ему канал доступа к дистрибьюторам к потребителям.

При низких темпах продаж продукции, а, следовательно, и невысокой прибыли появление новых товаропроизводителей не окажет сильного влияния на конкуренцию.

Если же предлагаемая ими новая продукция пользуется повышенным спросом у потребителей, а значит, обещает хорошие доходы, то появление новых соперников резко изменит конкурентную ситуацию. В тоже  время, чем сильнее угроза появления на рынке новых конкурентов, тем активнее действующим товаропроизводителям надо укреплять свои позиции, затрудняя  при этом проникновение на рынок новичков. Следует заметить, что большое влияние на конкуренцию между товаропроизводителями оказывают товары-заменители. Иногда продавцы конкурируют друг с другом, предлагая покупателям взаимозаменяемую продукцию.

Доступность товаров-заменителей побуждает потребителей сравнивать их с исходным товаром по качеству, и другим характеристикам имеющим спрос, а также по цене. Вообще проблема конкуренции, а также ее изучение количественными методами сложна и требует особого подхода, на котором мы остановимся в специальной работе. При моделировании конкуренции в настоящей работе нам хотелось бы акцентировать внимание, вот на каком моменте. При изучения многих экономических закономерностей и проблем конкуренции, а также их последствий удобным инструментарием является моделирование, трудности которого обычно возникают на содержательном уровне [1, 209c; 7, С. 10-12; 8, 710c. и др.,]

Согласно мнению Н.Н. Моисеева [9, С. 56-141] «эвристическая ценность модели, ее способность не только воспроизвести явление, изучение которого дало нам исходный материал для ее формирования, но и предсказать новые факты». Действительно, выразив какой либо процесс в виде совокупности формул, мы имеем возможность изучать (априори) не сам процесс, а эту совокупность формул, получая при этом новые гипотезы для изучения их на модели и проверки на практике. Приведем поучительный пример, приведенный Н.Н. Моисеевым [9, С. 56-141]. «Для того, чтобы, следуя Птолемею, описать траекторию планеты, необходим огромный экспериментальный материал, практически вся траектория. Согласно Ньютону, чтобы предсказать движение планеты, причем любой, не только тех, которые изучал Птолемей, достаточно знать только начальные положения и скорость. Значит, никаких временных рядов, никакой статистики, для исследования достаточно мгновенной фотографии». И еще: «Если исходные параметры (фазовые переменные) достаточно полно (с точки зрения целей исследования) характеризуют процесс, если все необходимые связи, введенные в модель, достаточно точно отражают реальность, если модель верифицирована, т.е. проверена на достаточно надежном экспериментальном материале, и если имеется достаточно надежная информационная база, то проблема ввода модели в машину и ее анализ – дело техники» (Моисеев [9, C.56-141].

Все это свидетельствует о том, что большое преимущество имеют те модели, которые могут использовать общие законы, а, следовательно, уменьшить к минимуму (не всегда) использование статистических методов. Мы, считаем, что для исследования многих экономических проблем, удобным обобщающим показателем, аккумулирующим на себя весь производственный процесс, является прибыль.

Первый вариант уравнений.

A;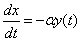

(1)

B; .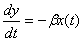

где α=p1v1 и β=p2v2. Коэффициенты p1, p2 v1 и v2  соответственно, вероятности покупки потребителями продукции у производителей S2 и S1 с соответствующими скоростями их обслуживания.

Допустим, что вероятность покупки товара и скорость обслуживание покупателей у производителей S1 и S2, также одинакова (феномен «нулевой конкуренции»). Тогда, решение системы уравнений А и В имеет вид,

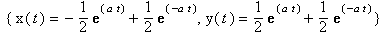                        (2),

Как следует из (1), объемы продаж у обоих производителей должны непрерывно (со временем) расти. Но сам процесс находится в противофазе, что подтверждает тот факт, что, искомая закономерность имеет неустойчивый, колебательный характер.

Равенства (2) можно преобразовать к гиперболическому виду, приняв при этом, что chx=(ex+e-x)/2, sh=(ex-e-x)/2 и при t=0, x=X0 и y=Y0 [2, С.180-182; 3, С. 260-264].

Опуская математическую сторону решения данной проблемы, мы приведем лишь те результаты преобразований искомых уравнений (они приведены в упомянутых выше монографиях) которые согласуются с нашими построениями о конкуренции среди мелких товаропроизводителей.

Оказывается, что средняя величина не реализованной продукции зависит только от приведенного времени T и от параметра k, характеризующий соотношение объемов предлагаемой рынку продукции, т.е.

k=(X0/Y0)√a/b                           (3).

Можно еще понимать под параметром k степень преимущества одного конкурента над другим. Допустим, что a=b=a. Тогда k=a(X0/Y0). Следовательно, преимущество, конкурента S1 над S2 будет зависеть от соотношения объемов предлагаемой потребителям соответствующей продукции, а при равенстве их объемов k=a конкуренции практически нет. Оба производителя имеют одинаковые шансы в продаже продукции. Ее скорость реализации зависит от параметра a. Если k>1, то преимущество в реализации своей продукции будет у товаропроизводителем S1 и он побеждает в данной борьбе. И обратно, если k<1, то выигрывает товаропроизводитель S2.

Приведем пример.

Пусть у товаропроизводителя S1 имеется 10т продукции, а у S2 -2т со скоростью обслуживания, соответственно v1=1 и v2 = 2 человека в минуту. Вероятность покупки продукции составила p1=0.5 и p2=0.2.

Параметр k =(10/2)√(1х0,5)/(2х0,45)=3,7. Видно, что первый предприниматель имеет большое преимущество в реализации своей продукции (в 3,7 раза) и с успехом способен победить своего конкурента. В заключении хотелось бы акцентировать внимание, вот на каком, моменте. Используя уравнения (1) можно изучить многие стороны конкурентных взаимодействий предпринимателей, не только на конкретном рынке, но, и исследовать взаимодействие групп рынков, как систем рыночной экономики. Это открывает новые перспективы в решении проблемы конкуренции. В данном случае, ее изучение выходит на новый уровень, т.е. с  применением к данному вопросу идей и методов синергетики.

Рассмотрим ситуацию, когда производители, реализуя свою продукцию (независимо от конкурента), все же испытывают его влияние на состояние общей выручки. Приведем, опубликованную в [7] систему уравнений, описывающих данное предположение.

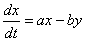
(4).

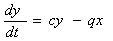
Первые два члена правой части уравнений (4) показывают, что при отсутствии конкуренции, увеличение продаж у обоих производителей будет увеличиваться. Ясно, что подобная ситуация не может стремиться к бесконечности. Пределы роста продаж, даже при отсутствии конкуренции, будут определяться спросом покупателей на эту продукции. В подобной ситуации ограничивающим фактором будет фактор превышение предложения над спросом. Можно полагать, что  «невидимая рука рынка « будет играть роль этого ограничения. Если, продифференцировать в (4) второе уравнение по 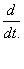, и преобразовать, то получим дифференциальное уравнение, приведенное в [7], вида,

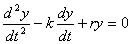                               (5).

где k (c+a) и r=(ac-qb).

В (5) y- отклонение колеблющейся продажи продукции от состояния равновесия; k - коэффициент ограничивающий скорость продаж. Он зависит от соотношения реализации продукции обеими предпринимателями, но без влияния на этот процесс эффекта конкуренции; r – коэффициент характеризующий  эффект наращивания скорости продаж, «восстановления.

Характеристическое уравнения для (5), следующее:

λ2  - λk + r=0                             (6),

Его корни (λ1 и λ2 ) исчисляют как;

λ1.2 =-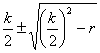                          (7).

Теория утверждает [5], что при решении (6) возможны различные подходы к анализу результатов исчислений. C ее аналитического построения  целесообразно рассмотреть различные случаи в зависимости от знака дискриминанта, вида:

D=k2-4r                     (8).

Если k2-4r>0, т.е. k2>4r, то отклонение системы (5) от точки равновесия (т.е. когда t→ ∞) стремится к минимуму. Этот процесс следует по экспоненциальному закону и без колебаний. Аналогичная закономерность будет наблюдаться и в отношении производителя S1.

Следовательно, при реализации продукции каждым из производителей, т.е. когда объемы продаж продукции ими велики, и не зависят от конкурента, колебания искомых процессов близки к нулю. Аналогичный случай будет иметь место и при  k2-r2=0.

Таким образом, анализ (4; 7) показывает, что при многовариантных сочетаниях коэффициентов a, b c и q можно получить представление о различных сценариях конкурентной борьбы в среде мелких товаропроизводителей, а также выявить условия устойчивости изучаемого процесса. В плане решаемой проблемы, считаем целесообразным акцентировать внимание еще на одном вопросе. Применение уравнений (1) позволяет исследовать не только возможные варианты результата взаимоотношений между конкурентами, но и выяснить роль новых их членов осваивающих рынок и влияющих на уровень конкуренции, а также покупателей. Тогда модель конкуренции можно свести к следующей системе уравнений:

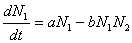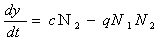,                        (8).

Первые два члена правой части уравнений (8) свидетельствуют о том, что при отсутствии конкуренции, увеличение продаж у обоих производителей будет непрерывно расти. Совсем другая ситуация возникнет, если между вновь осваивающими рынок товаропроизводителями (N2) и возникнет конкуренция (вторые члены правой части уравнений 8). Какие же в этом случае могут быть последствия для рыночной среды? 

Литература

1.Басовский Л.Е. Теория экономического анализа. М., «Инфа-М», 2008, 209с.

2. Вентцель Е.С. Введение в исследование операций. М.: «Советское радио», 1963, 384с.

3. Гутер Р.С., А.Р. Янпольский Дифференциальные уравнения. М: «Высшая школа», 1976, 303с.

4. Экономико-математическое моделирование (под общей ред. И.Н. Дрогобыцкого). М:. «Экзамен», 2006, 797с.

5. Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. М.: Наука, 646с.

6. Зульпукаров М.-Г.М., Чернавский Д.С., Щербаков А.В.Модель конкуренции (ресурс ИНТЕРНЕТ http://nonlih .ru/node/1198/)

7. Колесник Ю.А. Моделирование конкуренции в среде товаропроизводителей./Научно-аналитический журнал «Научная перспектива», № 4, С. 10-12, 2013.

8.. Кузнецов Б.Т. Математика. М.: «ЮНИТИ», 2004, 710с.

9. Моисеев Н.Н. Динамика биосферы и глобальные модели. М., Знание //Число и мысль, вып. 5, 1982, С.56-141.

10. Третьяк  Н.А. Конкуренция: проблемы, оценки и регулирования. Саратов, 2012, 196с.