К.э.н. Карапейчик И.Н.

ПАО «Азовмаш»

Экономический и производственный потенциал предприятия

Автором в большом цикле публикаций (см., в частности, [2-8]) развивается (с акцентом на объекты микроэкономического уровня и, в частности, промышленные предприятия) концепция потенциалов как способности, отражающей максимально возможный результат имманентно присущей соответствующему субъекту экономики деятельности.

Анализ потенциала предприятий как признака, определенного таким образом, а также как объекта измерений, послужил основанием для определения экономического потенциала как потенциала высшего уровня иерархии для произвольного хозяйствующего субъекта и введения понятия потенциальной функции предприятия Y как функции, отражающей зависимость максимально возможного чистого дохода (либо аналогичного, выражающего внутренне присущие предприятию экономические устремления показателя) от параметров  состояния предприятия и внешней среды его функционирования:

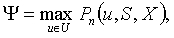                                               (1)

где S, X – векторы параметров состояния предприятия и внешней экономической среды соответственно; u – вектор управляющих переменных (пространство которых U является подпространством пространства S); U – множество допустимых векторов управляющих переменных [2, 8].

Таким образом, графиком потенциальной функции Y является множество

{Y(S, X), S, X},

представляющее собой всевозможные сочетания оптимальных значений целевой функции (чистого дохода) оптимизационной модели предприятия и соответствующих им комбинаций значений параметров (равновесного) состояния предприятия и параметров внешней среды.

В настоящем исследовании справедливость этого утверждения анализируется на примере экономического и производственного потенциалов, опираясь на общепринятые представления математической экономики и, в частности, теории фирмы [9].

В теории производства базовыми понятиями являются понятия чистого выпуска y и технологического множества Y, определяющего всевозможные   допустимые преобразования производственных факторов в продукцию предприятия [9], а технологические условия производства задаются с помощью ограничения вида

yÎY.                                                            (2)

Очевидно, технологии, использование которых приводит к большим по сравнению с другими технологиями затратам ресурсов при равном либо меньшем чистом выпуске, не представляют интерес. В связи с этим при изучении поведения предприятий можно ограничиться только технологически эффективными векторами чистой продукции.

Вектор y1 называется технологически эффективным, если он принадлежит множеству Y возможных векторов чистой продукции, и если в Y не существует другого вектора y2 такого, что

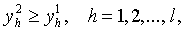
yÎY.                                                               

Множество технологически эффективных векторов Y*, таким образом, является подмножеством Y в пространстве благ либо совпадает с ним (Y*ÍY) [9].

В теории производства для описания технологических множеств предприятий наиболее широкое распространение получил аппарат производственных функций.

Производственная функция f для предприятия есть по определению действительная функция, определенная на Rl, такая, что

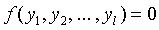                                                (3)

тогда и только тогда, когда вектор y является эффективным, и такая, что

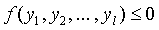                                                (4)

тогда и только тогда, когда вектор y принадлежит Y [9].

Выражение (3) является наиболее общей формой представления производственных функций. Для задания производственных функций применяются и формы (2), (4).

Если предположить, что предприятие выпускает только один вид продукции y1, то производственную функцию можно представить в следующем виде:

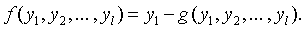                                 (5)

а технологические ограничения – в виде

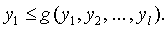                                               (6)

В практике экономико-математического моделирования наиболее часто производственная функция трактуется более узко и определяется как функция g выпуска продукции b1 в зависимости от затрат первичных ресурсов (a1, …, al):

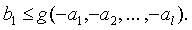                                             (7)

или, при изменении обозначений, как

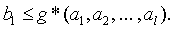                                              (8)

В наиболее простом случае, когда для производства продукции b1 благо первого вида a1 не используется, производственная функция записывается так:

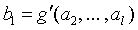                                                  (9)

или, с применением более традиционных для теории производственных функций обозначений, так:

y = f (x),                                                        (10)

где f – производственная функция; y – объем выпуска продукции; x – вектор затрат факторов производства (производственных ресурсов).

Графиком производственной функции (10) является множество

{(y, x)ÎR1´X | y = f(x)}

в пространстве R1´X, представляющее собой границу технологического множества

{(y, x)ÎR1´X | y £ f(x)}.

Таким образом, производственные функции вида (3), а также, как частный случай, вида (9), (10) характеризуют предельные (в смысле оптимальности по Парето) производственные возможности предприятия. (Заметим, что к такому же выводу пришел и автор работы [1], проводя на уровне математических рассуждений аналогию между потенциалами в физике и экономике.)

Эти представления полностью укладываются в концепцию потенциала,  изложенную выше, и обнаруживают тот факт, что производственные функции есть не что иное, как потенциальные функции, отражающие производственный потенциал предприятия.

В самом деле, имманентно присущей для любого производства деятельностью на уровне промышленных предприятий является производство (выпуск) продукции. Результатом производства в общем случае, т.е. для многономенклатурного производства, является вектор выпуска. Зависимость предельных объемов выпуска продукции (максимально возможный результат такой деятельности) от состояния исключительно производственных факторов и характеризуют производственные функции.

Рассмотрим сходство и различия между потенциальной Y и производственной f функциями на более формальном уровне.

Очевидно, что составляющей поведения предприятия (одними из компонент вектора S – аргумента потенциальной функции Y) является структура выпуска (объемы производства продукции всех видов) q, которая, в свою очередь, зависит от объемов использования производственных ресурсов x. Следовательно, и функция Y, и функция f являются функциями от x. Однако, если для производственной функции структура выпуска q является значением, то для функции, характеризующей экономический потенциал предприятия, структура выпуска q является одним из промежуточных звеньев, предопределяющих максимальный чистый доход.

Таким образом, производственные функции характеризуют исключительно производственные возможности предприятия, задавая закон преобразования производственных ресурсов в максимально возможный выпуск продукции, а потенциальные функции экономического потенциала – максимально возможный чистый доход, обусловленный, наряду со всеми  прочими факторами, производственными возможностями предприятия.

Литература:

1. Вереникин А.О. Теория экономического потенциала и ее аналог в математической физике // Экономические проблемы инновационного развития : монография / Под ред. К.А.Хубиева. – М.: ТЕИС, 2009. – 699 с. – Режим доступа: http://verenikin.professorjournal.ru/c/document_library/get_file?uuid=1d97b05b-b784-452a-a53a-a16620801057&groupId=456709.

2. Карапейчик И.Н. Анализ потенциальных функций предприятия методами классификации / И.Н. Карапейчик // Вісник Хмельницького національного університету. – 2013. – Т. 2. Економічні науки, № 3. – С. 85-93.

3. Карапейчик И.Н. Классификации потенциалов в экономике: критический взгляд / И.Н. Карапейчик // Вісник Хмельницького національній університету. – 2012. – № 2, Т. 3, Економічні науки. – С. 116-125.

4. Карапейчик И.Н. Классификация потенциалов экономических субъектов:  методологические аспекты и возможные решения / И.Н. Карапейчик // Актуальні проблеми економіки. – 2013. – № 1(139). – С. 20-31.

5, Карапейчик И.Н. Оценка инновационного потенциала машиностроительных предприятий : монография / Карапейчик И.Н. – Мариуполь: "Новый мир", 2011. – 184 с.

6. Карапейчик И.Н. Понятие потенциала в экономике: задачи и направления исследований / И.Н. Карапейчик // Актуальні проблеми економіки. – 2012. – № 7 (133). – С. 16-25.

7. Карапейчик И.Н. Понятие потенциала в экономике: общая концепция / И.Н. Карапейчик // Ефективна економіка. – 2011. – № 12. – Режим доступа к журн.: http://www.economy.nayka.com.ua/index.php?operation=1&iid=820.

8. Карапейчик И.Н. Потенциальные функции и задача систематизации потенциалов в экономике / И.Н. Карапейчик // Інноваційні економіка. – 2012. – № 4(30). – С. 9-15.

9. Маленво Э. Лекции по микроэкономическому анализу / Маленво Э. – М.: Наука, 1985. – 390 с.