д.т.н., профессор. Пиль Э.А., Санкт-Петербургский государственный морской технический университет, Россия

Использование программы «Регресиия» для прогноза численности населения республики Сейшельские острова

Для анализа и прогноза численности населения Республики Сейшельские Острова была использована программа «РЕГРЕССИЯ», которая позволяет провести регрессионный анализ по 16 видам уравнений (см. табл. 1), а также получить значения переменных «a» и «b» и коэффициент корреляции R2.

1.				y = a + bx	9.	y = axb
2.	y = 1/(a + bx)	10.	3.	y = a + b/x	11.	y = a + b∙ln(x)
4.	y = x/(a + bx)	y = a/(b + x)
5.	y = a∙bx	13.	y = ax/(b + x)
6.	y = a∙exp(bx)	14.	y = a∙exp(b/x)
7.	y = a∙10(bx)	15.	y = a∙10(b/x)
8.	y = 1/(a + b∙exp(-x))	16.	y = a + b∙xn

На основе произведенных расчетов, было показано, что из 16 видов уравнений можно использовать только 9, которые и представлены в табл. 2 совместно с их коэффициентами корреляции R2

Таблица 2. Уравнения и значения коэффициентов корреляции
№	Уравнение	R2	№	Уравнение	R2
1	y = a + bx	0,9959	6	y = a/(b + x)	-0,9973
2	y = a + b/x	-0,996	7	y = a∙exp(b/x)	-0,9984
3	y = a∙exp(bx)	0,9967	8	y = a∙10(b/x)	-1,000366
4	y = a∙10(bx)	0,9969	9	y = a + b∙xn	0,9922
5	y = a + b∙log(x)	0,8654	-	-	-

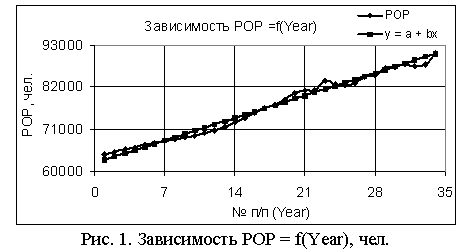
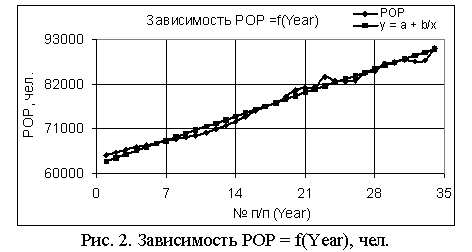
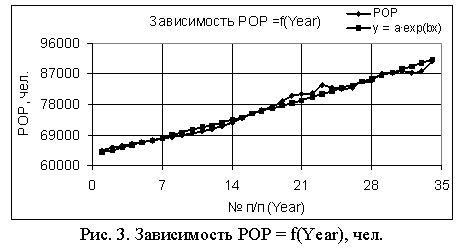
В следующей табл. 3 показаны статистические (столбец 2) и расчетные (столбцы 3, 5 и 7) значения численности населения, а также погрешность расчетов.

Табл. 3. Статистические и расчетные значения численности населения их погрешность

№	Год	Насел., чел	y=a+bx	Погр.	y=a+b/x	Погр.	y=a∙exp(bx)	Погр.
	1	2	3	4	5	6	7	8
1	1980	64400	63022	-2,14	62962	-2,23	63676	-1,12
2	1981	65127	63862	-1,94	63813	-2,02	64388	-1,13
3	1982	65780	64701	-1,64	64664	-1,70	65108	-1,02
4	1983	66366	65540	-1,25	65514	-1,28	65837	-0,80
5	1984	66901	66379	-0,78	66362	-0,81	66573	-0,49
6	1985	67400	67218	-0,27	67210	-0,28	67317	-0,12
7	1986	67877	68057	0,27	68057	0,27	68070	0,28
8	1987	68352	68896	0,80	68904	0,81	68832	0,70
9	1988	68847	69735	1,29	69749	1,31	69602	1,10
10	1989	69387	70574	1,71	70594	1,74	70380	1,43
11	1990	70000	71413	2,02	71437	2,05	71167	1,67
12	1991	70754	72253	2,12	72280	2,16	71963	1,71
13	1992	71656	73092	2,00	73122	2,05	72768	1,55
14	1993	72711	73931	1,68	73963	1,72	73582	1,20
15	1994	73924	74770	1,14	74804	1,19	74405	0,65
16	1995	75304	75609	0,40	75643	0,45	75237	-0,09
17	1996	76417	76448	0,04	76482	0,08	76078	-0,44
18	1997	77319	77287	-0,04	77320	0,00	76929	-0,50
19	1998	78846	78126	-0,91	78157	-0,87	77790	-1,34
20	1999	80410	78965	-1,80	78993	-1,76	78660	-2,18
21	2000	81131	79804	-1,64	79828	-1,61	79540	-1,96
22	2001	81202	80643	-0,69	80662	-0,66	80429	-0,95
23	2002	83700	81483	-2,65	81496	-2,63	81329	-2,83
24	2003	82800	82322	-0,58	82329	-0,57	82238	-0,68
25	2004	82500	83161	0,80	83161	0,80	83158	0,80
26	2005	82900	84000	1,33	83992	1,32	84088	1,43
27	2006	84600	84839	0,28	84822	0,26	85029	0,51
28	2007	85033	85678	0,76	85652	0,73	85980	1,11
29	2008	86956	86517	-0,50	86480	-0,55	86941	-0,02
30	2009	87298	87356	0,07	87308	0,01	87914	0,71
31	2010	87977	88195	0,25	88135	0,18	88897	1,05
32	2011	87441	89034	1,82	88961	1,74	89891	2,80
33	2012	87784	89874	2,38	89787	2,28	90897	3,55
34	2013	90846	90713	-0,15	90611	-0,26	90611	-0,26

Как видно из табл. 3. были получены очень высокие значения коэффициентов корреляции и, соответственно, небольшие значения погрешности, что дает нам сделать вывод о возможности прогнозирования численности населения Сейшельских Островов с высокой точностью. На основе значений табл. 3 были построены рис. 1-3.