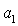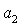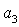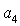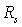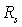К.э.н. Булгакова И.Н.

Воронежский государственный университет, Россия

Интегральная оценка эффективности функционирования промышленных кластеров

Существует несколько подходов к построению интегральных оценок, характеризующих особенности функционирования экономического объекта. Все они строятся на основе экономических показателей, отражающих различные стороны деятельности.

Рассмотрим отдельно рейтинговую оценку, представленную формулой (1). Оценка имеет вид:

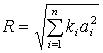                                                  (1)

где 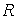 - обобщающая рейтинговая оценка,

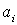- значение i-го финансового показателя,

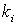- весовые коэффициенты при 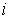-м показателе,  .

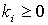Весовые коэффициенты в этой модели могут быть выбраны несколькими способами: во-первых, на основе статистической информации; во-вторых, можно считать, что все показатели равноценны, .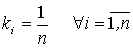

Согласно подходу, описываемому в [2], все финансовые показатели разбиты на четыре группы, характеризующие такие стороны хозяйственной деятельности, как прибыльность, эффективность управления, деловая активность, ликвидность.

Но, как оговорено в [2], убыточные предприятия в данной системе не рассматриваются. Это является существенным недостатком предлагаемой оценки. На практике возникает необходимость определения общей тенденции в изменении финансового положения экономического объекта на протяжении нескольких периодов. Расчет показателей 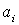 ведется для каждого периода и может возникнуть ситуация, когда в один из периодов большая часть показателей  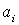(или все) окажутся отрицательными. Было бы логичным заключить, что в данном случае анализируемое предприятие отклоняется от траектории стабильного развития. Однако оценка (1) не отражает этого перехода. Происходит искажение информации из-за структуры самой оценки. Рейтинг предприятия при  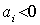будет необоснованно высоким.

Предлагается некоторая модификация рейтинговой оценки (1), которая учитывает возможность применения как положительных, так и отрицательных показателей. Предлагаемая оценка имеет вид:

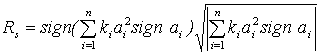                    (2)

Рассмотрим 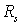 как функцию аргумента 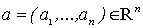. Функция  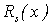непрерывна при любых 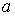. Рассмотрим ее дифференциальные свойства. Область 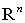разбивается на три различные области:  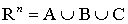, которые пересекаются только по границе. Определим эти области:

1. 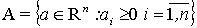. Эта область ограничена координатными гиперплоскостями 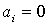. В ней мы получаем традиционную оценку (3.6).

3. 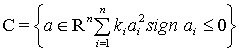. В области  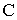преобладают отрицательные показатели.

Граница 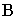 и 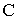 кроме координатных гиперплоскостей состоит из поверхностей вида  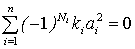 (например, ).

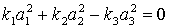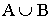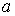Внутри множества  функция  принадлежит классу непрерывно дифференцируемых функций, т.е. изменения  относительно  носят плавный характер. При пересечении границы  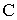производные  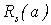терпят разрыв второго рода (обращаются в бесконечность), что свидетельствует о резком характере изменений 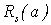, а, следовательно, и рейтинговой оценки предприятия.

Анализ стабильности развития экономического объекта, проводимый при помощи других интегральных оценок, позволяет разбить исследуемые предприятия на три группы: обладающих устойчиво стабильным состоянием, с признаками напряженности и с неудовлетворительным положением и отсутствием перспектив его стабилизации. Можно предположить, что разделение множества 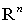 на три множества  также характеризует различную степень стабильности предприятия.

Оценим с помощью (1) и (2) деятельность конкретного экономического объекта. Выберем в качестве экономических показателей:

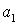- показатель ликвидности,

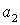- показатель прибыльности,

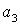- показатель устойчивости,

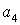- показатель активности.

Числовые значения показателей и расчетные значения оценок (1) и (2) приведены в таблице 1. В качестве 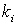 возьмем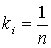 , где 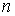- количество показателей.

Таблица 1 – Основные показатели, характеризующие ЗАО «Воронежская хлебная компания»

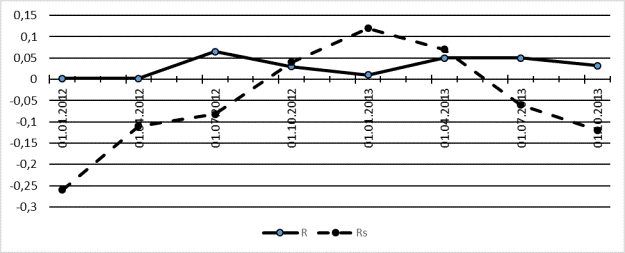
Более наглядно разница между двумя рейтинговыми оценками представлена на графике.

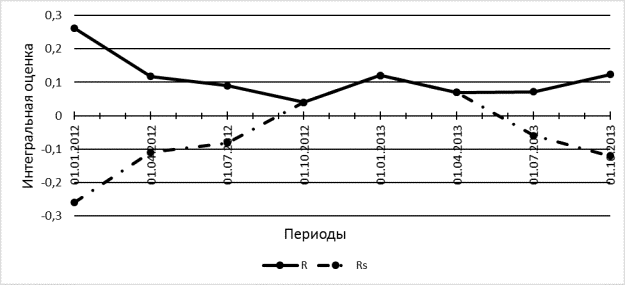
Рисунок1 - Сравнительные характеристики рейтинговых оценок

Таким образом, оценки, полученные с помощью формулы (2) дают более полную характеристику эффективности функционирования экономического объекта, учитывая спады и подъемы хозяйственной деятельности.

При анализе деятельности отдельно взятого предприятия целесообразно рассматривать его в совокупности со всей интегрированной структурой. Такое рассмотрение позволяет сравнить характеристики данного предприятия с аналогичными характеристиками кластера в целом и определить, в чем причина успеха или неудачи данного предприятия, если его характеристики выше (ниже) кластерных.

Расчет рейтинговой оценки отдельно взятого предприятия (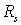) и расчет рейтинговой оценки с использованием средних показателей по кластеру в целом (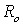) приведены в таблице 2. Динамика эконмической деятельности  предприятия представлено графически на рис. 2.

Сравнительные характеристики предприятий в разрезе анализа функционирования кластерной структуры в целом можно получить с помощью адаптивно-имитационной модели оценки риска [1], если в качестве 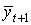 взять среднее значение оценки (2) по все кластеру промышленных предприятий в момент времени  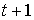и соответственно

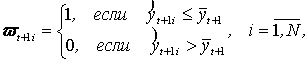
где 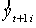 — результат 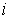-го имитационного эксперимента.

Тогда 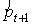 — риск отклонения от общей кластерной оценки в «худшую» сторону:

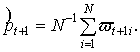
1. Булгакова И.Н., Давнис В.В. Использование адаптивно-имитационных моделей в качестве индикатора финансово-экономической устойчивости предприятия // Известия РАЕН. МММИУ. - Т.4, 2000 г., № 4. - С. 112-118.