Численный анализ устойчивости в линейной модели конкурентного взаимодействия

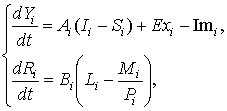i=1…n,

где все параметры и переменные i-й экономики положительны и означают:

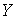– национальный доход;

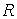– процентную ставку;

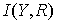– функцию спроса на инвестиции (

);

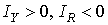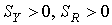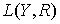– суммарный спрос на деньги (

);

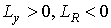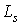– предложение денег (фиксированная величина);

A,B – положительные параметры адаптации и реакции.

Эта система отражает тот простой факт, что превышение спроса на инвестиции над сбережениями приводит к возрастанию дохода, и наоборот; и что если спрос на деньги выше, чем их предложение, то ставка процента прибыли растет.

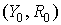, систему в локальной области пространства вблизи равновесия и наличие циклов в этой модели, первым рассмотрел Торре[2]. Чтобы воспользоваться бифуркационной теоремой Хопфа, он определил условия существования пары чисто мнимых собственных значений и выяснил, когда равновесие теряет устойчивость. Очевидно, что для уединенной экономики (n=1) никаких особенностей сложнее предельного цикла быть не может. Там же показано, что международная торговля между экономиками, в которых наблюдаются предельные циклы, может привести к появлению странного аттрактора и, следовательно, возникновению хаоса. Международную торговлю в некотором смысле можно рассматривать как возмущения изолированных экономик [3]. Этот подход предложен Лоренцем. Расширенная система (1) состоит из n связанных ограниченных осцилляторов. Как показано Ньюхаусом, Рюэлем и Такенсом, возмущение движения по трехмерным торам может привести к странному аттрактору [3,4]. Таким образом, в международной модели было установлено существование странных аттракторов. Все ранее сказанное относится к нелинейным системам.

В настоящей работе показано, что аналогичные явления происходят и когда система (1) линейна с постоянными коэффициентами и решение для нее ищется в виде

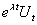. Если отношение периодов иррационально, то движение – хаотическое, при этом легко видеть, что две точки, в начальный момент времени лежащие рядом, с течением времени могут оказаться сколь угодно далеко [5].

В работе проверяется следующее утверждение.

Если все автономные экономики принадлежат к осцилляторному типу, то начиная с n=2, введение международной торговли может привести в линейном приближении как к общему росту, так и коллапсу одной из экономик, или к появлению странного аттрактора в объединенной экономике.

Имеем периодические, либо непериодические движения, которые в ограниченной области, сходятся к аттрактору, не являющемуся точкой или циклом. Лоренц показал [2], что существование хаотических траекторий в соответствующих моделях можно установить численным моделированием, что и сделано в данной работе средствами пакета Mathematica.

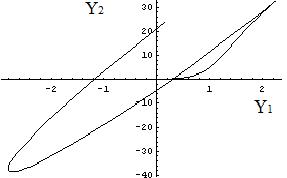
Рис. 1 Взаимные колебания и рост национальных доходов в связанных торговлей экономиках .

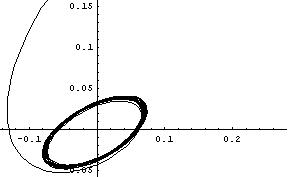
Рис.2 Зависимость переменных – национального дохода и процентной ставки одной из стран.

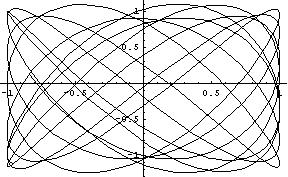
Рис.3 Хаотические колебания национальных доходов.

Промоделированы все случаи нарушения устойчивости экономик при введении торговых связей. Полученные результаты проиллюстрированы на проекциях 4-х мерного фазового пространства.

Литература:

1. Тарасевич Л.С., Гальперин В.М., Гребенников П.И., Леусский А.И. Макроэкономика / Общая редакция Л.С. Тарасевича. - СПб.: Издательство СПбГУЭФ, 1999. – 654 с.

2. Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории. – М.: Мир, 1999. – 335с.

3. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент. / Введение в нелинейную динамику. – М.: Эдиториал УРСС, 2002. – 256с.

4. Арнольд В.И. Дополнительные главы теории обыкновенных дифференциальных уравнений. – М.: Наука, 1987. – 304с.

5. AlRefai W.A. Mathematical model of chaos, caused by international trade / Технологический аудит и резервы производства, Том 5, № 4(13) 2013. – С. 6-7.