К.э.н. Бермухамедова Г.Б.

Каспийский государственный университет технологии и инжиниринга им.Ш.Есенова

Экономико-математические методы, применяемые в анализе хозяйственной деятельности предприятия

Математические   методы   опираются   на  методологию  экономико-математического моделирования  и  научно  обоснованную классификацию задач анализа хозяйственной деятельности. 

В настоящие время в анализе хозяйственной деятельности организаций все большее применение находят математические методы исследования. Это способствует совершенствованию экономического анализа, его углублению и повышению его действенности.

В результате использования математических методов достигается более полное изучение влияния отдельных факторов на обобщающие экономические показатели деятельности организаций, уменьшение сроков осуществления анализа, повышается точность осуществления экономических расчетов, решаются многомерные аналитические задачи, которые не могут быть выполнены традиционными методами. В процессе использования экономико-математических методов в экономическом анализе осуществляется построение и изучение экономико-математических моделей, описывающих влияние отдельных факторов на обобщающие экономические показатели деятельности организаций.

Различают четыре основных вида экономико-математических моделей, используемых при анализе влияния отдельных факторов:

Аддитивные модели могут быть определены как алгебраическая сумма отдельных показателей. Такие модели могут быть охарактеризованы с помощью следующей формулы:

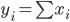
Примером аддитивной модели является баланс товарной продукции.

П = К В,

Кратные модели — это соотношение отдельных факторов. Они характеризуются такой формулой:

ОП = x/y

Здесь ОП представляет собой обобщающий экономический показатель, который находится под влиянием отдельных факторов x и y. Примером кратной модели может служить формула, выражающая зависимость между продолжительностью оборота оборотных активов в днях, средней величиной этих активов за данный период и однодневным объемом продаж:

П = ОА/ОП,

Смешанные модели — это сочетание уже рассмотренных нами видов моделей. Так, например, такой моделью может быть описан показатель рентабельности активов, на уровень которого влияют три фактора: чистая прибыль (ЧП), величина внеоборотных активов (ВА), величина оборотных активов (ОА):

В обобщенном виде смешанная модель может быть представлена такой формулой:

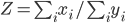
Итак, вначале следует построить экономико-математическую модель, описывающую влияние отдельных факторов на обобщающие экономические показатели деятельности организации. Большое распространение в анализе хозяйственной деятельности получили многофакторные мультипликативные модели, так как они позволяют изучить влияние значительного количества факторов на обобщающие показатели и тем самым достичь большей глубины и точности анализа.

После этого нужно выбрать способ решения этой модели. Традиционные способы: способ цепных подстановок, способы абсолютных и относительных разниц, балансовый способ, индексный метод, а также методы корреляционно-регрессионного, кластерного, дисперсионного анализа, и др. Наряду с этими способами и методами в экономическом анализе используются и специфически математические способы и методы.

Интегральный метод экономического анализа. Одним из таких способов является интегральный. Он находит применение при определении влияния отдельных факторов с использованием мультипликативных, кратных, и смешанных моделей.

В условиях применения интегрального метода имеется возможность получения более обоснованных результатов исчисления влияния отдельных факторов, чем при использовании метода цепных подстановок и его вариантов. Метод цепных подстановок и его варианты, а также индексный метод имеют существенные недостатки: 1) результаты расчетов влияния факторов зависят от принятой последовательности замены базисных величин отдельных факторов на фактические; 2) дополнительный прирост обобщающего показателя, вызванный взаимодействием факторов, в виде неразложимого остатка присоединяется к сумме влияния последнего фактора. При использовании же интегрального метода этот прирост делится поровну между всеми факторами.

Интегральный метод устанавливает общий подход к решению моделей различных видов, причем независимо от числа элементов, которые входят в данную модель, а также независимо от формы связи между этими элементами.

Интегральный метод факторного экономического анализа имеет в своей основе суммирование приращений функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках.

В процессе применения интегрального метода необходимо соблюдение нескольких условий. Во-первых, должно соблюдаться условие непрерывной дифференцируемости функции, где в качестве аргумента берется какой-либо экономический показатель. Во-вторых, функция между начальной и конечной точками элементарного периода должна изменяться по прямой Ге . Наконец, в третьих, должно иметь место постоянство соотношения скоростей изменения величин факторов

dy / dx = const

При использовании интегрального метода исчисление определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования осуществляется по имеющейся стандартной программе с применением современных средств вычислительной техники.

Если мы осуществляем решение мультипликативной модели, то для расчета влияния отдельных факторов на обобщающий экономический показатель можно использовать следующие формулы:

Z=xy;

ΔZ(x) = y0 *Δx + 1/2Δx *Δy

Z(y)=x0 * Δy +1/2Δx * Δy

При решении кратной модели для расчета влияния факторов воспользуемся такими формулами:

Z=x /y;

ΔZ(x) = Δx/Δy Ln y1/y0

ΔZ(y)=ΔZ - ΔZ(x)

Существует два основных типа задач, решаемых при помощи интегрального метода: статический и динамический. При первом типе отсутствует информация об изменении анализируемых факторов в течение данного периода. Примерами таких задач могут служить анализ выполнения бизнес-планов либо анализ изменения экономических показателей по сравнению с предыдущим периодом. Динамический тип задач имеет место в условиях наличия информации об изменении анализируемых факторов в течение данного периода. К этому типу задач относятся вычисления, связанные с изучением временных рядов экономических показателей.

Таковы важнейшие черты интегрального метода факторного экономического анализа. Метод логарифмирования. Кроме этого метода, в анализе находит применение также метод логарифмирования. Он используется при проведении факторного анализа, когда решаются мультипликативные модели. Сущность рассматриваемого метода заключается в том, что при его использовании имеет место логарифмически пропорциональное распределение величины совместного действия факторов между последними, то есть эта величина распределяется между факторами пропорционально доле влияния каждого отдельного фактора на сумму обобщающего показателя. При интегральном же методе упомянутая величина распределяется между факторами в одинаковой мере. Поэтому метод логарифмирования делает расчеты влияния факторов более обоснованными по сравнению с интегральным методом.

В процессе логарифмирования находят применение не абсолютные величины прироста экономических показателей, как это имеет место при интегральном методе, а относительные, то есть индексы изменения этих показателей. К примеру, обобщающий экономический показатель определяется в виде произведения трех факторов — сомножителей f = x y z.

Найдем влияние каждого из этих факторов на обобщающий экономический показатель. Так, влияние первого фактора может быть определено по следующей формуле:

Δfx = Δf · lg(x1 / x0) / lg(f1 / f0)

Каким же было влияние следующего фактора? Для нахождения его влияния воспользуемся следующей формулой:

Δfy = Δf · lg(y1 / y0) / lg(f1 / f0)

Наконец, для того, чтобы исчислить влияние третьего фактора, применим формулу:

Δfz = Δf ·lg(z1 / z0)/ lg(f1 / f0)

Таким образом, общая сумма изменения обобщающего показателя расчленяется между отдельными факторами в соответствии с пропорциями отношений логарифмов отдельных факторных индексов к логарифму обобщающего показателя.

При применении рассматриваемого метода могут быть использованы любые виды логарифмов — как натуральные, так и десятичные.

Метод дифференциального исчисления. При проведении факторного анализа находит применение также метод дифференциального исчисления. Последний предполагает, что общее изменение функции, то есть обобщающего показателя, подразделяется на отдельные слагаемые, значение каждого из которых исчисляется как произведение определенной частной производной на приращение переменной, по которой определена эта производная. Определим влияние отдельных факторов на обобщающий показатель, используя в качестве примера функцию от двух переменных.

Задана функция Z = f(x,y). Если эта функция является дифференцируемой, то ее изменение может быть выражено следующей формулой:

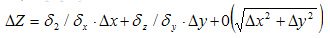
Поясним отдельные элементы этой формулы:

ΔZ = (Z1 - Z0) - величина изменения функции;

Δx = (x1 - x0) — величина изменения одного фактора;

Δy = (y1 - y0) -величина изменения другого фактора;

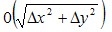- бесконечно малая величина более высокого порядка, чем

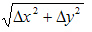
В данном примере влияние отдельных факторов x и y на изменение функции Z (обобщающего показателя) исчисляется следующим образом:

ΔZx = δZ / δx · Δx; ΔZy = δZ / δy · Δy.

Сумма влияния обоих этих факторов — это главная, линейная относительно приращения данного фактора часть приращения дифференцируемой функции, то есть обобщающего показателя.

В условиях решения аддитивных, а также кратно-аддитивных моделей для исчисления влияния отдельных факторов на изменение обобщающего показателя используется также способ долевого участия. Его сущность состоит в том, что вначале определяется доля каждого фактора в общей сумме их изменений. Затем эта доля умножается на общую величину изменения обобщающего показателя.

Такова сущность способа долевого участия, используемого для целей факторного анализа. Практическое  использование  теории экономико-математических моделей в организации которое позволяет   развивать   традиционные  методы  финансово-хозяйственной деятельности,  адаптировать  их  к  новым  потребностям учета неопределенности в будущем основных показателей деятельности предприятий.

Литература:

1. Е. Н. Ломкова, А. А. Эпов, Экономико-математические модели управления производством. Учебное пособие. ВолгГТУ, Волгоград, 2005. 2. А.В. Стариков, И.С. Кущева, Экономико-математическое и компьютерное моделирование.Учебное пособие / Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2008. 3. Воронин А. А., Губко М. В., Мишин С. П., Новиков Д. А. Математические модели организаций: Учебное пособие, М.: ЛЕНАНД, 2008. - 360 с.