Модели формирования оптимальной структуры портфеля ценных бумаг для коммерческих банков

Именно портфель ценных бумаг является тем инструментом, с помощью которого может быть достигнутое необходимое соотношение всех инвестиционных целей, которые недосягаемо из позиции отдельно взятой ценной бумаги, и возможно только при их комбинации.

Портфели ценных бумаг коммерческих банков является частью взаимозависимой системы портфелей более высокого уровня. Функционирование всей системы портфелей подчиняется интересам обеспечения стабильности и рентабельности института, обеспечение стабильности всей финансовой системы.

К моделям, получившие наибольшее распространение и используемые для формирования оптимальной структуры портфеля ценных бумаг, относятся модели Марковица, Блэка и Шарпа.

Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, принесенный финансовым инструментом, как случайную переменную, т.е. доходы по отдельным инвестиционным объектам случайно изменяются в некоторых границах. Тогда, если определить по каждому инвестиционному объекту определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. По модели Марковица определяются показатели, которые характеризуют объем инвестиций и риск, что позволяет сравнивать между собой разные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать меру оценки разных комбинаций. Как меру ожидаемого дохода из ряда возможных доходов на практике используют наиболее возможное значение, которое в случае нормального распределения совпадает с математическим ожиданием.

Для измерения риска служат показатели рассеяния, поэтому чем больший разброс величин возможных доходов, тем большая опасность, который ожидаемый доход не будет получен. Мерой рассеяния является среднеквадратичное отклонение. Рассматривая теоретически предельный случай, при котором в портфель можно включать неконченое количество ценных бумаг, дисперсия (мера риска портфеля) ассимптотично будет приближаться к среднему значению ковариации.

Общий риск портфеля можно разложить на две составные части: рыночный риск, который нельзя исключить и которому подвластны все ценные бумаги практически в равной мере, и собственный риск, который можно избегнуть с помощью диверсификации. При этом сумма вложенных средств по всем объектам должна равнять общему объему инвестиционных вложений, т.е. сумма относительных долей в общем объеме должна сравниваться единицы.

Проблема заключается в численном определении относительных долей акций и облигаций в портфеле, которые наиболее удобные для владельца. Марковиц ограничивает решение модели тем, что из всего множества «допустимых» портфелей, т.е. из тех, что удовлетворяют ограничение, необходимо выделить те, которые являются более рисковыми, чем другие. С помощью разработанного Марковицем метода критических линий можно выделить бесперспективные портфели. Таким образом остаются только эффективные портфели. Отобранные таким образом портфели объединяют в список, который содержит сведения о проценте состава портфеля из отдельных

Объяснение факта, что инвестор должен рассмотреть только множество

возможных портфелей, приходится в следующей теореме об эффективном множестве: «Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает максимальную ожидаемую прибыльность для некоторого уровня риска и минимальный риск для некоторого значения ожидаемой прибыльности». Набор портфелей, которые удовлетворяют этим двум условиям, называется эффективным множеством.

Для выбора наиболее приемлемого для инвестора портфеля ценных бумаг используют кривые безразличия. В этом случае эти кривые отображают в графической форме преимущество инвестора. Если рассматривать в графической форме отношения инвестора к риску и прибыльности, откладывая по горизонтальной оси риск, мерой которого является среднеквадратичное отклонение (sp), а по вертикальной оси – вознаграждение, мерой которого является ожидаемая прибыльность (rp), то можно получить семейство кривых безразличия. Имея информацию об ожидаемой прибыльности и стандартных отклонениях возможных портфелей ценных бумаг, можно построить карту кривых безразличия, которое отображает преимущества инвесторов (рис. 1). Каждая из указанных на рис. 1 позиций инвестора к риску характерна тем, что любое уменьшение их риска обозначается на сокращении прибыльности и стандартном отклонении каждого из портфелей. И поскольку портфель содержит в себе набор разных бумаг, то целиком понятной есть зависимость его от ожидаемой прибыльности и стандартного отклонения каждой ценной бумаги, которая входит в портфель. Инвестор должен выбирать портфель, который лежит на кривой безразличии, расположенной выше и левее всех других кривых. В теореме об эффективном множестве утверждается, что инвестор не должен рассматривать портфели, которые не лежат на левой верхней границе множества достижимости, которые являются ее логическим следствием. Исходя из этого, оптимальный портфель находится в точке соприкосновения одной из кривых безразличия наиболее эффективного множества. Построение кривых безразличия является сложной задачей. На практике ее часто получают в косвенной или приближенной форме путем оценки уровня толерантности риска, обусловленной как наибольший риск, что инвестор готов принять для данного увеличения ожидаемой прибыльности.

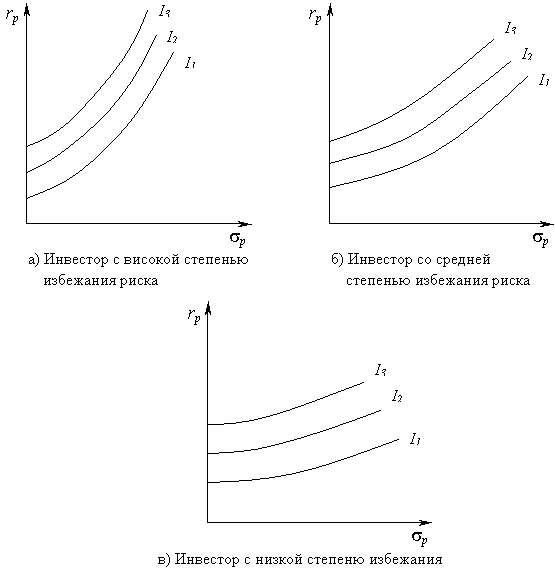
Рисунок 1 – Кривые безразличия инвесторов

Поэтому, с точки зрения методологии, модель Марковица можно определить как практически-нормативную, что не означает навязывания инвестору определенного стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы показать, как поставленные цели достижимые на практике.

Модель Блэка аналогична модели Марковица, но в отличие от последней в ней отсутствующее условие неопровержимости на части активов портфеля. Это означает, что инвестор может делать короткие продажи, т.е. продавать активы, предоставленные ему в виде займа. В этом случае инвестор рассчитывает на снижение курса ценной бумаги и планирует возвратить заем теми же ценными бумагами, но приобретенными по более низкому курсу. Вследствие отсутствия ограничений на части активов в портфеле потенциальная прибыль инвестора не ограничена максимальной прибыльностью одного из активов, которые входят в портфель.

Американский экономист Шарп предложил индексную модель. Причем он не разработал нового метода составления портфеля, а упростил проблему таким образом, которое приближенное решение может быть найдено со значительно меньшими усилиями. Шарп ввел фактор, который играет особую роль в современной теории портфеля – показатель «бета», который характеризует степень риска бумаги и показывает, в сколько раз изменение цены бумаги превышает изменение рынка в целом. Если «бета» больше единицы, то данная бумага можно отнести к инструментам с повышенной степенью риска, так как ее цена движется в среднем быстрее рынке. Если «бета» меньше единицы, то степень риска этой бумаги относительно низкий, поскольку на протяжении периода расчета ее цена изменялась медленнее, чем рынок. Если «бета» меньше нуля, то в среднем движение этой бумаги было противоположным движения рынка на протяжении периода расчета.

В индексной модели Шарпа используется тесная корреляция между изменением курсов отдельных акций. Предполагается, что необходимые входные данные можно приблизительно определить с помощью базисного фактора и отношений, которые связывают его с изменением курсов отдельных акций. Статистическая процедура для получения таких апостериорных значений показателя «бета» представляет собой простую линейную регрессию или метод наименьших квадратов. На западных рынках значения данного показателя регулярно рассчитываются для всех ценных бумаг и публикуются вместе с индексами. Пользуясь этой информацией, инвесторы могут сформировать собственный портфель ценных бумаг.