К.т.н. Заика И.В,
д.т.н. Ромм Я.Е.
Излагается построение программной схемы локализации экстремумов функций в произвольной области определения. Эта задача классифицируется как задача оптимизации и имеет многообразные приложения в математических моделях экономики. Помимо того, на данной основе (как минимумы модулей) вычисляются нули полиномов. Как следствие, вычисляются корни характеристических полиномов матрицы. В математической экономике большую роль играют так называемые продуктивные матрицы. Программное вычисление собственных значений матрицы позволит сделать вывод о ее продуктивности.
Метод основан на применении внутренней адресной сортировки по ключу (ниже сортировки), сохраняющей порядок равных элементов. Пусть вначале рассматривается функция одной действительной переменной
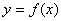у которой требуется определить все экстремумы на произвольно заданном промежутке, входящем в область ее определения. Строится равномерная сетка. В узлах сетки считываются значения функции, они принимаются за элементы сортируемого массива
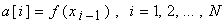. (2)
Массив (2) сортируется. Для определенности взята сортировка подсчетом изложенной в [1]. Тогда условие локализации всех минимальных элементов последовательности (2) примет вид
где
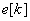– элемент массива индексов на выходе сортировки. Смысл условия (3) в том, что в
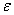-окрестности входного элемента с индексом
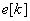нет элемента в отсортированном массиве, превосходящего элемент с этим индексом.
Присоединение условия локализации к программе сортировки массива (2) дает устойчивую локализацию минимумов функции (1) [1].
Для локализации и вычисления нулей функции достаточно на вход сортировки подать абсолютные величины значений функции.
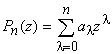, у которого могут быть комплексные нули и комплексные коэффициенты. Умножив его на комплексно-сопряженное значение, получим функцию
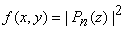. Очевидно, нахождение нулей
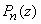сводится к нахождению нулей функции
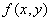от двух действительных переменных. Таким образом, комплексные нули многочленов ищутся как минимумы модуля этих многочленов по схеме, описанной выше схеме [2].
Локализация и вычисление собственных значений матриц. Будем искать собственные значения матрицы
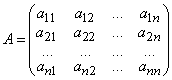
с учетом кратности. Для их программного определения необходимо предварительное вычисление коэффициентов характеристического полинома из левой части уравнения
.
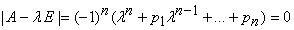Для этого используется метод Леверье ввиду невосприимчивости к частным особенностям матрицы и простоты программной реализации. Метод Леверье содержит следующие операции [3]: построение степеней матрицы
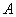от первой до
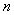-ной включительно; вычисление следов этих степеней; решение системы уравнений Ньютона:
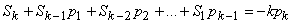, где
,
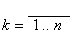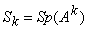– след матрицы
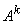. Программу выполнения метода Леверье можно дополнить оценками области расположения нулей полинома [3].
Приложение метода к экономическим исследованиям. Описанный метод нахождения собственных значений матрицы может использоваться, например, в динамической модели В. Леонтьева, определяющей траектории сбалансированного экономического развития. Качественные свойства этих траекторий зависят от матриц
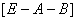, где
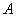– матрица прямых затрат,
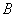– матрица коэффициентов капиталоемкости,
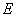– единичная матрица.
В математической экономике большую роль играют так называемые продуктивные матрицы. Программное вычисление собственных значений матрицы
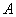позволит сделать вывод о продуктивности этой матрицы. Доказано, что матрица
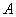является продуктивной тогда и только тогда, когда все собственные значения этой матрицы по модулю меньше единицы.
В заключение отметим, что по всем описанным выше схемам оптимизации, поиска нулей, экстремумов и собственных значений проводились численные и программные эксперименты. Результаты экспериментов [2, 3] устойчиво подтверждают надежность и практическую реализуемость предложенных схем в достаточно общих условиях.
Литература:
1. Ромм Я.Е, Заика И.В. Схема поиска экстремумов и нулей функций на основе адресной сортировки / ТГПИ. – Таганрог, 2005. – 50 с. Деп. В ВИНИТИ 01. 03. 2005, № 289-В2005.
2. Ромм Я.Е. Метод вычисления нулей и экстремумов функций на основе сортировки с приложением к поиску и распознаванию. II // Кибернетика и системный анализ. – 2001. – № 5. – С. 81 – 101.
3. Ромм Я.Е. Соловьёва И.А. Метод программного определения нулей и полюсов функций с учетом кратности в приложении к цифровой фильтрации // Фундаментальные и прикладные проблемы приборостроения, информатики, экономики и права: Научные труды VII Международной научно- практической конференции. – С. 178 – 183.