О развитии теории финансовых инвестиций с фиксированным доходом

Дальнейшее развитие теория получила в работах [5 - 8]. Получены математические доказательства зависимости дюрации облигации, продающейся с дисконтом, от срока до погашения [5]; зависимости цены облигации от частоты купонных платежей [6]; влияния уровня доходности рынка [7] и срока до погашения [8] на изменчивость цены облигации. Такие задачи в существующей литературе ранее не рассматривались. Справедливость доказанных утверждений подтверждается конкретными вычислениями и рыночными наблюдениями. Доказательства получены при тех же условиях, что и в работах [2,3]. Это условия определенности. В связи с этим предложенные доказательства можно рассматривать как дополнение теории финансовых инвестиций с фиксированным доходом в условиях определенности.

Заметим, что математическое доказательство какого-либо свойства облигации требует решения определенной математической задачи. Задачи, которые пришлось решать при изучении указанных зависимостей, имеют свои особенности. Рассмотрим некоторые из них.

В работе [6] рассмотрена задача о влиянии частоты купонных выплат на цену облигации, где котируемая цена облигации P(m) рассматривается как функция числа купонных платежей m в году:

P(m) = +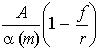

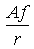Здесь α(x)= 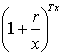− функция, определенная на множестве x ≥ 1, а Т, f , r, А – фиксированные параметры облигации. Для решения задачи потребовалось воспользоваться свойствами функции α(x) =

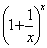на множестве x ≥ 1. Известно, что

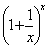= e. Монотонность этой функции установлена для целочисленного положительного аргумента в теории числовых последовательностей. Более подробно свойства этой функции в литературе не упоминаются. В связи с этим были доказаны следующие утверждения о функции α(x):

1) функция α(x) является возрастающей и вогнутой на множестве x ≥ 1;

2) абсолютное изменение функции α(x) при увеличении x на 1 тем больше, чем меньше x: Δα(x1) > Δα(x2), где 1 ≤ x1 < x2;

3) относительное изменение функции α(x) при увеличении x на 1 тем больше, чем меньше x: 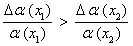, где 1 ≤ x1 < x2.

Доказательства этих утверждений получены с помощью разложений функций в степенные ряды, теорем о дифференцируемых функциях и теорем выпуклого анализа [9]. Решение этой вспомогательной задачи само по себе представляет интерес и дополняет теорию функций.

На основании свойств функции α(x) в работе [6] доказаны теоремы о влиянии числа купонных платежей в году на цену облигации. Такой фактор, как число купонных платежей в году, не относится к основным факторам, влияющим на цену облигации. Однако, к примеру, авторы Интернет-ресурса [10] отмечают: «Увеличение частоты купонных выплат повышает инвестиционную привлекательность выпуска». Таким образом, на практике проявляется влияние этого фактора на инвестиционные свойства облигации. В связи с этим рассмотренная в [6] задача представляет как теоретический, так и практический интерес.

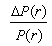при изменении ее доходности. По величине

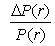оценивают чувствительность цены облигации к изменению рыночной процентной ставки на заданную величину, то есть процентный риск облигации − одну из важнейших её характеристик как объекта инвестирования. Влияние срока до погашения на изменчивость цены облигации известно по рыночным наблюдениям. Однако задача о влиянии этого фактора на изменчивость цены купонной облигации ранее не рассматривалась. Для ее решения потребовалось предварительно установить влияние уровня доходности рынка на величину изменения цены облигации при изменении ее срока до погашения на один купонный период. В существующей литературе такая задача тоже ранее не рассматривалась. Например, при увеличении рыночной процентной ставки на Δr > 0 необходимо рассмотреть поведение последовательности

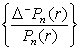, где

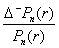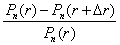– относительное снижение цены облигации, r – исходный уровень доходности, n – число купонных периодов, оставшихся до погашения облигации. В случае, когда, например, f < r (облигация продается с дисконтом) при сравнении n-го и (n – 1)-го членов последовательности имеем:

−

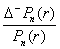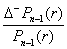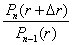
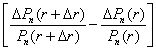где 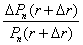и

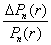− относительные изменения цены облигации при уменьшении срока до погашения на один купонный период при уровнях доходности (r + ∆r) и r соответственно. Чтобы установить влияние уровня доходности рынка на относительное изменение цены облигации при изменении ее срока до погашения на один купонный период, доказана следующая теорема.

При фиксированном n > 1 справедливы следующие утверждения:

1) ΔРn и 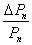являются убывающими функциями доходности r на отрезке 0 ≤ r ≤ f (облигация продается с премией при r < f и по номиналу при r = f);

2) существуют точки максимумов ra функции ΔРn и ro функции 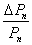(при фиксированном n > 2) на множестве r ≥ f (облигация продается с дисконтом при r > f ).

Абсолютное ΔРn и относительное 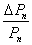изменения цены облигации при уменьшении срока до погашения на один купонный период рассматриваются как функции доходности r. Для доказательства утверждений теоремы использованы достаточные условия монотонности и глобального экстремума дифференцируемой функции.

Одно из доказательств этой теоремы приведено в работе [7], другое – в работе [8]. При доказательстве в работе [7] использовано свойство дюрации Маколея, доказанное ранее автором в работе [5]. В результате доказательств получены две различные формулы для приближенного значения точки ro. Однако вычисления по обеим формулам дают близкие значения, что указывает на согласованность доказательств. Данная теорема сама по себе представляет интерес. Она является естественным продолжением одной из известных рыночных теорем, сформулированных в работе [1].

Как видим, решение основной задачи и в этом случае потребовало решения вспомогательной задачи в виде доказательства приведенной теоремы. На базе данной теоремы в работе [8] доказана теорема о влиянии срока до погашения на изменчивость цены облигации. Наиболее часто наблюдаемая зависимость процентного риска облигации от срока до погашения – чем больше срок до погашения, тем больше процентный риск облигации. Для облигаций, продающихся с дисконтом, доказано наличие срока, за пределами которого процентный риск облигации начинает уменьшаться. Такое поведение процентного риска довольно редко наблюдается на рынке. По мнению автора, это можно объяснить тем, что сроки до погашения значительной части облигаций меньше указанного срока. Кроме того, необходимо учесть условия, при которых получены доказательства: горизонтальность кривой рыночных доходностей и параллельность ее перемещений. В реальности кривая доходностей не является горизонтальной и ее сдвиги не обязательно параллельны.

Рассмотрены некоторые задачи в теории финансовых инвестиций с фиксированным доходом в условиях определенности. Как видим, применение математических методов способствует развитию этой теории и одновременно - углублению знаний об инвестиционных свойствах облигации. В результате увеличивается способность данной теории выполнять основную свою функцию - возможность понимать, объяснять и прогнозировать поведение облигации как объекта инвестирования. При этом, конечно, необходимо учитывать условия, при которых получены результаты в теории.

ЛИТЕРАТУРА

1. Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. – М.: Инфра-М, 1999.

2. Барбаумов В. Е., Гладких И. М., Чуйко А. С. Финансовые инвестиции. – Ч. 1. Инвестиции с фиксированными доходами: учебное пособие. – М. : Изд-во Рос. экон. акад., 2000.

3. Мельников А. В., Попова Н. В., Скорнякова В. С. Математические методы финансового анализа. – М.: Анкил, 2006.

4. Попова Н.В. Рыночные теоремы как математические. Материалы международной V‌ІІI научно-практической конференции «Образование и наука XXI века - 2012», 17-25 октября 2012г. Республика Болгария, София: «Бял ГРАД-БГ» ООД.

5. Попова Н. В. О некоторых свойствах дюрации Маколея // Вестник финансового университета. – 2011. – № 1 (61).

6. Попова Н.В. Влияние частоты купонных платежей на цену облигации // Вестник финансового университета. – 2012. – № 3 (69).

7. Попова Н.В. Рыночные теоремы и их продолжение // Вестник РЭУ им. Г.В. Плеханова. – 2013. – № 7(61).

8. Попова Н.В. Влияние срока до погашения на изменчивость цены облигации // Вестник финансового университета. – 2013. – № 3(75).

9. Попова Н.В. Показательно-степенная функция в задаче о цене облигации. Материалы VIII международной научно-практической конференции «Теория и практика современной науки». 26-27 декабря 2012 г. Москва: «Институт стратегических исследований».

10. Размещение рублевых облигационных займов URL: http://www.besteconomics.ru (дата обращения 17.03.2012).