Имашева А.О., заведующая лабораторией мониторинга условий труда РГКП «Республиканский научно-исследовательский институт по охране труда Министерства труда и социальной защиты населения Республики Казахстан», Астана (Казахстан)

Математическое моделирование в управлении охраной труда

Ключевые слова: метод управления охраной труда; математическая модель; вредные производственные факторы; оценка профессионального риска; коэффициент эластичности.

Проблема обеспечения безопасности человека на производстве почти всегда решается в условиях ограниченных экономических возможностей. Отсюда вытекает необходимость в разработке таких методов управления охраной труда, которые позволили бы получать управленческие решения, обеспечивающие максимум социального эффекта при ограниченных ресурсах. Реализация такого подхода возможна только через построение и исследование соответствующих математических моделей, учитывающих конкретные условия производства.

В рыночных условиях возможно проведение оценки профессионального риска в конкретных организациях, поскольку работодатель обязан проводить аттестацию рабочих мест по условиям труда, информировать работников об условиях и охране труда на рабочих местах, о существующем риске повреждения здоровья. Однако, корреляционные связи факторов условий труда с показателями здоровья работников изучены пока недостаточно. Необходимо располагать конкретными информативными показателями интенсивности воздействия факторов условий труда, дозы неблагоприятного воздействия опасных и вредных факторов, которые должны быть доступными для расчета и основываются на сведениях о фактических значениях факторов производственной среды на рабочих местах, полученными в результате мониторинга условий труда, то есть аттестации рабочих мест по условиям труда [1].

Применяемые математические методы вычислений при оценке профессионального риска просты и не нуждаются в каких-либо детальных пояснениях, однако методологические принципы анализа риска заслуживают того, чтобы отметить здесь их особенности.

Методология оценки профессионального риска с применением математических методов имеет  ряд преимуществ по сравнению с другими методами. Она дает быстрый, простой, понятный ответ о воздействии неблагоприятных факторов окружающей среды и может использоваться там, где не собираются регулярно данные об уровнях воздействия, нет данных о здоровье работников и др [2].

Для достижения поставленной цели необходимо:

• собрать исходные данные;
• обработать исходные данные, вычисленить статистические параметры;
• построить матрицу парных коэффициентов корреляции;
• проверить матрицу парных коэффициентов корреляции на наличие  мультиколлинеарности;
• отобрать факторы для включения в модель;
• построить многофакторную математическую модель;
• проверить значимость множественного коэффициента корреляции и уравнения множественной регрессии по F– критерию Фишера;
• вычислить коэффициенты эластичности и ранжирование выявленных производственных факторов.

Далее рассмотрим подробнее каждый из этапов в отдельности.

Сбор исходных данных. Моделирование предъявляет жесткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначенных для практического использования. При этом принимается во внимание не только принципиальная возможность подготовки информации (за определенные сроки), но и затраты на подготовку соответствующих информационных массивов. Эти затраты не должны превышать эффект от использования дополнительной информации.

В процессе подготовки информации широко используются методы теории вероятностей, теоретической и математической статистики [3, 4].

Обработка исходных данных, вычисление статистических параметров, построение матрицы парных коэффициентов корреляции. Определив исходные данные, исследователь переходит непосредственно к обработке информационного массива. Смысл того или иного преобразования исходных данных заключается в изменении характера эмпирического распределения с тем, чтобы привести его в соответствие с целью исследования.

Статистический параметр средних величин – это обобщающий показатель совокупности однотипных явлений по какому-либо количественному показателю. Цели определения средних величин это ослабление влияния случайных факторов на изучаемый показатель; получение сводного показателя, описывающего данную совокупность в целом.

Для построения матрицы используются парные коэффициенты корреляции (или коэффициент корреляции Пирсона), разработанные в 90-х годах XIX века Карл Пирсоном, Фрэнсис Эджуортом и Рафаэль Уэлдоном. Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать в конце XIX века английский биолог и статистик Фрэнсис Гальтон [5].

Проверка матрицы парных коэффициентов корреляции на наличие мультиколлинеарности. Для обнаружения мультиколлинеарности не существует никаких точных критериев, применяется лишь ряд эмпирических методов. При этом анализируется корреляционная матрица независимых переменных и в модель включаются только те факторы, которые более сильно связаны с результативным показателем.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими социально-экономическими явлениями.

Излишняя сложность и громоздкость модели ведет к затруднениям в расчетах и интерпретации полученных результатов. Нужно учитывать не только реальные возможности информационного и математического обеспечения, но и сопоставлять затраты на моделирование с получаемым эффектом (при возрастании сложности модели прирост затрат может превысить прирост эффекта).

Построение многофакторной модели. Для нахождения зависимости уровня заболеваемости от вредных производственных факторов нами будет использован многофакторный корреляционно-регрессионный анализ. Этот анализ сводится к решению следующих задач:

• обосновать взаимосвязи факторов, влияющих на исследуемый показатель;
• определить степень влияния каждого фактора на результат, который позволит установить, в каком направлении и на какую величину изменится результативный показатель при изменении каждого фактора, входящего в модель;
• количественно оценить тесноту связи между результативным показателем и факторами.

Параметры многофакторной модели, т.е. уравнения регрессии, найденные на основе имеющихся у исследователя данных, называют оценками параметров.

Наиболее простым методом, применяющимся для оценки параметров множественной модели, является метод наименьших квадратов (МНК). Для того чтобы МНК-оценки параметров был несмещенным, эффективным и состоятельным, необходимо выполнение определенных требований, называемых предпосылками МНК. Эти требования касаются статистических свойств исходных данных:

• факторы являются неслучайными величинами, не связанными между собой;
• результат является случайной величиной, не ограниченной сверху или снизу;
• для каждого конкретного значения факторов результат рассматривается как отдельная случайная величина;
• различные случайные величины Yi и Yj  независимы друг от друга: .

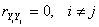Метод наименьших квадратов может быть применен к моделям регрессии, линейным по параметрам. Если функция регрессии нелинейная по параметрам, необходима ее предварительная линеаризация [6].

Проверка значимости множественного коэффициента корреляции и уравнения множественной регрессии по F–критерию Фишера. Для оценки значимости многофакторной модели используют F-критерий Фишера. Сравнивают фактическое и табличное значения F-критерия, найденным для df1= m и df2 = n – m – 1 степеней свободы, где m – число факторов, n – число наблюдений. Если фактическое значение больше табличного, уравнение регрессии следует признать статистически значимым  с вероятностью 0,95.

Вычисление коэффициентов эластичности и ранжирование выявленных производственных факторов. Так как параметры множественной модели (аi – коэффициенты многофакторной модели) определяются различными единицами измерения фактором и поэтому не сравнимы между собой. Таким образом, для сопоставления факторов по силе влияния необходимо использовать относительные показатели силы связи – коэффициенты эластичности.

Этапы построения множественной регрессии и вычисления коэффициентов эластичности приведены на рисунке 1.

В качестве примере рассмотрим данные исследуемого предприятия, изучение влияния на количество заболевших (у, чел.) различных производственных факторов: влажность воздуха (х1, %), шум (х2, дБА), пыль (х3, мг/м3). Данные приведены после экспоненциального сглаживания в таблице 1.

Для сокращения трудоемкости расчетов, концентрируясь при этом на содержательных вопросах моделирования, исследователю достаточно задать лишь общий алгоритм решения и применить возможности стандартной программы MS Excel. Надстройка Пакет анализа данных (Analysis ToolPak) которая позволяет решать самые различные задачи, связанные со сложным математическо-статистическим анализом данных.

Использование Пакет анализа данных начинается  с введением исходных данных на рабочем столе программы MS Excel. Далее следует выполнить команду Сервис ® Анализ данных. На экране появится диалоговое окно Анализ данных (Data Analysis) [7].

Таблица 1.  Исходные данные для построения модели

Матрица парных коэффициентов корреляции между факторами х1, х2, х3 равна

.

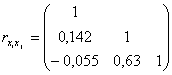Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. В данном случае совокупное воздействие факторов друг на друга отсутствует.

Математическая модель после нахождения параметров, применяя МНК, будет иметь вид

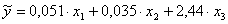         (1).

Вычисленное с помощью программы MS Excel фактическое значение F-критерия равно 11,04. Сравниваем его с табличным, найденным для df1= m и df2 = (n – m – 1) степеней свободы, где m= 3– число факторов, n=18 – число наблюдений (кол-во профессий и должностей). Для модели (1) табличное значение F-критерия при df1= 6 и df2 = (18 – 3 – 1) = 14 степенях свободы и уровне значимости a = 0,05 равно 3,34.

Так как фактическое значение F-критерия больше табличного, модель следует признать статистически значимой с вероятностью 0,95.

Теперь проверим адекватность полученной многофакторной модели. Вычисленный с помощью программы MS Excel коэффициент множественной корреляции равен 0,83. Его значение близко  к 1. Это свидетельствует о том, что учтены все факторы, влияющие на количество заболевших и полученная многофакторная модель (1) адекватно к исследуемому явлению.

Величины абсолютных показателей силы связи определяются единицами измерения факторов и поэтому не сравнимы между собой. Для сопоставления факторов по силе влияния используют относительные показатели силы связи – коэффициенты эластичности.

Коэффициент эластичности при факторе х3 показывает, что при изменении значения пыли на 1% от своего среднего уровня значения количество заболевших в среднем изменится в ту же сторону на 0,36% от своего среднего уровня при фиксированном значений остальных факторов.

Таким же образом объясняется значение остальных рассматриваемых производственных факторов.

Сравнивая эти коэффициенты эластичности между собой, можно сделать вывод о том, что производственный фактор-пыль более сильно влияет на количество заболевших, на втором месте – влажность воздуха и на третьем месте – шум.

Таким образом, методологии оценки профессионального риска с применением математических методов позволят определить приоритетные направления для разработки мероприятий по профилактике и снижению уровня вредных производственных факторов и профессионального риска. Ранжирование производственных факторов по приоритетам особенно важно в условиях ограниченности ресурсов.

Список литературы

1. Охрана труда. Курс лекций для руководителей и специалистов служб охраны труда. / Под ред. Л.П. Шариковой. – Нижний Новгород: Биота-плюс, 2007. – 172 с.

2. Бурков, В.Н. Экономико-математические модели управления развитием отраслевого производства / В.Н. Бурков, Г.С. Джавахадзе. – М.: ИПУ РАН, 1997, 64 с.

3. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Проспект, 2009. – 288 с.

4. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – Учебное пособие для вузов. 10-е издание, стереотипное. – М.: Высшая школа, 2004. – 479 с.

5. Общая теория статистики: Учебник / Под ред. Р.А. Шмойловой. – 3-е издание, переработанное. – М.: Финансы и Статистика, 2002.  – 560 с.

6. Асаев, Р.А. Эконометрия / Р.А. Асаев, К.А. Ахметов, А.О. Имашева, Г.К. Шалгынбаева. – Алматы: Агроуниверситет, 2007. – 231 c.

7. Долженков, В. Microsoft Excel 2000. / В. Долженков, Ю. Колесников. – СПб.: БХВ – Санкт-Петербург,1999. – 1088с.