Практический аспект разрешимости модели Гордона с учетом реинвестирования части прибыли в производство

Теоретически, расчетная формула примет вид:

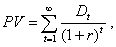(1)

где РV – текущая рыночная цена акции; D1, D2, D3, … - последовательные годовые выплаты дивидендов; r - ставка дисконтирования.

Получается, что уравнение (1) сложно практически использовать, поскольку для него нужна оценка всех будущих дивидендных выплат.

Известная модель Гордона [1] эту ситуацию существенно упрощает, предполагая, что в будущем дивиденды будут увеличиваться с постоянной скоростью. В этом случае формула (1) примет вид:

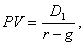(2)

где g – темп прироста дивидендов.

В модели (2) мы предполагали, что рыночная цена обыкновенной акции определяется только благодаря такому источнику доходов как дивидендные платежи.

На практике же часть чистой прибыли корпорация расходует на выплату дивидендов акционерам, а часть чистой прибыли реинвестируется в производство для получения будущих доходов. Как в этом случая будет выглядеть известная модель Гордона? Как рост доходов, создаваемых путем реинвестирования в производство будущих доходов и распределение полученных доходов, будет влиять на стоимость фирмы? Попытаемся в этом разобраться.

В дальнейшем будем использовать следующие обозначения: Pt - цена акции в момент время t ; Dt - дивиденд на акцию в t году; Et - прибыль на акцию в год t.

Введем следующие количественные показатели:

1.Коэффициент реинвестирования b – доля чистой прибыли, используемой на реинвестирование (b=(E-D)/E);

2.Коэффициент выплаты дивидендов (c=1-b) – доля чистой прибыли, расходуемая на выплату дивидендов (с=D/E);

Предположим, что все доходы выплачиваются в виде дивидендов, т.е. нет реинвестирования и роста дивидендов. Подставляя в модель Гордона (2) E=D1 и g=0, получим формулу приведенной стоимости такой акции:

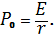(3)

Тогда из (3) имеем:

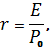(4)

т.е. уровень рыночной капитализации в этом случае равен отношению чистой прибыли на одну акцию к ее рыночной цене.

Теперь предположим, что корпорация удерживает часть чистой прибыли для реинвестирования ее в производство будущих доходов.

Если эта доля b не изменяется со временем, то дивиденд на акцию Dt в момент время t будет определяться следующим образом:

. (5)

Допустим, что доходность от реинвестирования в производства для получения будущих доходов k известна. Посмотрим, как будет происходить изменение показателей прибыли на акцию и дивидендов на акцию в течение ряда лет. При этом будем предполагать, что все новые инвестиции финансируются только за счет нераспределенной части прибыли, и, следовательно, исключаем всякую возможность заимствований.

1-й год: Корпорация получила прибыль Е, выплатила дивиденды в размере (1-b)E и выделила для реинвестирования bE.

2-й год: Поскольку доходность от реинвестирования в производство составляет k, то корпорация за второй год получила прибыль в размере E+ kbE, или (1+kb)E. Тогда сума выплаченных дивидендов в нашем случае будет составлять (1-b)(1+kb)E. Таким образом, для реинвестирования будет выделено сумма b(1+kb)E.

3-й год: Теперь прибыль составит E+kbE+kb(1+kb)E=(1+kb)2E. Тогда в виде дивидендов будет выплачено (1-b)(1+kb)2E, а на реинвестирование будет выделено b(1+kb)2E .

Продолжая аналогичные рассуждения для любого момента времени t, заметим, что величина дивидендных платежей увеличивается с постоянной скорость g=kb. Тогда модель Гордона (2) будет иметь вид:

(6)

Сделав ряд алгебраических преобразований в уравнении (6), будем иметь:

(7)

Попробуем истолковать полученный результат.

Если доходность от реинвестирования k равна показателю рыночной капитализации r , по которой инвесторы дисконтируют будущие доходы, то приведенная стоимость акции P0 всегда постоянна, независимо от доли нераспределенной прибыли. В этом случае уравнение (7) сводится к уравнению (3), т.е. к ситуации, когда все доходы расходуются на выплату дивидендов и отсутствует рост доходов корпорации.

Второй член уравнения (7) будет всегда положителен когда

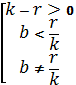, (8)

т.е. руководство корпорации должно браться за тот инвестиционный проект, доходность которого от реинвестирования k превосходит показателя рыночной капитализации r.

Следовательно, вторую часть уравнения (7) можно рассматривать как часть стоимости акции, которую инвестор готов платить за потенциал будущего роста корпорации, т.е. рыночная стоимость данной акции может быть определена уравнением (6) или (7).

Продолжим исследования уравнения (7). Вторая часть этого уравнения также положительна, когда справедлива следующая система

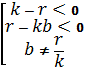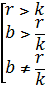или . (9)

Так как r>k , следовательно r/k> 1, а 0<b<1 (доля чистой прибыли, используемая на реинвестирование), то второе неравенство данной системы никогда невыполнимо. Таким образом, система (9) в этом случае неразрешима.

Итак, уравнение (7) справедливо тогда и только тогда, когда доходность от реинвестирования k превосходит показателя рыночной капитализации r.

Литература

1.Ченг Ф.Ли, Джозеф И. Финнерти. Финансы корпораций. Теория, методы и практика. Учебник для вузов. Пер. с англ. -М.: ИНФА, 2000, 685 с.