Закирова У.В., Осечкина Т.А.
Пермский национальный исследовательский политехнический университет, Россия
Модификация сбалансированного алгоритма решения задачи инкассации
При инкассации объектов возникает большое разнообразие ограничений [1], например, вместимость транспортного средства или период времени, за который необходимо обслужить тот или иной объект. А также при рассмотрении крупных городов возникает проблема большого объема обслуживающихся точек. Данные проблемы вызывают трудности при выборе метода решения.
Задачу инкассации можно трактовать, как классическую задачу маршрутизации транспорта [2]. Введем основные обозначения модели: переменная
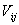 обозначает расстояние между клиентом
обозначает расстояние между клиентом 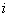 и клиентом
и клиентом 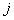 ;
; 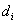 - количество кассет с наличностью, которое необходимо погрузить или выгрузить с объекта
- количество кассет с наличностью, которое необходимо погрузить или выгрузить с объекта 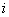 . Параметр
. Параметр 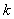 отражает номер автомобиля и пишется верхним индексом. Переменная
отражает номер автомобиля и пишется верхним индексом. Переменная 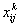 является булевой переменной: если
является булевой переменной: если 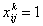 , то это означает, что клиент
, то это означает, что клиент 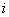 предшествует
предшествует 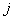 , а если
, а если 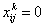 , то наоборот. Переменная
, то наоборот. Переменная 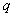 - вместимость одного транспортного средства.
- вместимость одного транспортного средства.
Таким образом, исходя из данных обозначений, запишем математическую модель задачи:
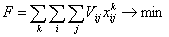 (1)
(1)
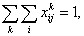
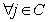 (2)
(2)
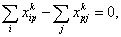
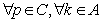 (3)
(3)
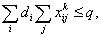
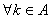 (4)
(4)
Целевая функция (1) определяет затраты на каждый маршрут для всех транспортных средств. Ограничение (2) означает, что каждый клиент обслуживается только один раз и одним транспортным средством, (3) – автомобиль покидает вершину 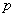 , только если он заранее прибыл в нее. Ограничение (4) означает, что транспортное средство не может обслужить больше клиентов, чем позволяет его грузоподъемность, а (5) – бинарная переменная.
, только если он заранее прибыл в нее. Ограничение (4) означает, что транспортное средство не может обслужить больше клиентов, чем позволяет его грузоподъемность, а (5) – бинарная переменная.
Данная задача относится к NP-трудных задач. Методы решения таких задач разделяют на точные, эвристические и метаэвристические методы [3]. Точные методы основаны на полном переборе всех возможных решений, что, в свою очередь, делает их неэффективными [4]. Эвристические методы производят относительно ограниченный поиск решений и обычно находят довольно хорошее решение за приемлемое время. Но данные методы также обладают недостатком, а именно, они являются приблизительными [4]. Метаэвристические - самые эффективные, но в данных методах есть параметр, который напрямую влияет на результат, исходя из входных данных [5], и на практике приходится каждый раз отлаживать этот параметр заново.
Помимо основных методов существует новый подход к решению задач маршрутизации транспорта, основанный на понятии сбалансирования уровня загрузки транспортных средств. Данный метод подробно рассмотрен в диссертации [6]. В данной работе предлагается использовать принцип дихотомического деления вершин на группы для каждого транспортного средства. Поскольку на каждом этапе вызывается рекурсивная процедура, которая делит все рассматриваемые вершины пополам, то это отражается на времени решения. А если заранее узнать количество маршрутов, и модифицировать данный алгоритм, то сократится время расчетов и решение не потеряет точности.
В классическом методе предполагается, что матрица расстояний симметрична, что редко встречается на практике. При приведении несимметричной матрицы к симметричной известными методами теряется точность.
В настоящей работе предпринята попытка учесть все неудобства рассмотренных методов, и представлена блок-схема (рис. 1), которая отражает все процедуры, которые необходимо провести, чтобы найти приближенное решение поставленной задачи.
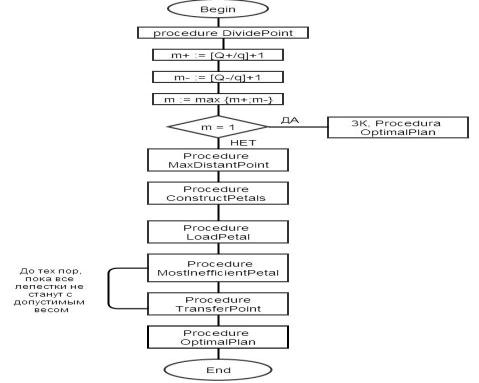
Рассмотрим более подробно блок-схему. Procedure DividePoint делит все множество точек на две группы с положительным весом (это тот вес, который необходимо погрузить в машину) и отрицательным (напротив, выгружается из машины). При этом накапливаются 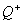 и
и 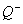 для того, чтобы понять какое минимальное количество маршрутов необходимо (
для того, чтобы понять какое минимальное количество маршрутов необходимо (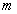 ), чтобы обслужить рассматриваемую область.
), чтобы обслужить рассматриваемую область.
Далее основываясь на количестве маршрутов, строятся m лепестков, при помощи procedure MaxDistantPoint. Каждый лепесток определяется одной самой удаленной точкой, которая находится, исходя из максимальной суммы расстояний от этой точки до депо и до других ранее найденных. Назовем эти точки базовыми. После определения базовых точек, необходимо сформировать каждый лепесток при помощи procedure ConstructPetals. Для каждого из оставшихся объектов находятся суммы расстояний от данного объекта до депо и до каждой из базовых точек. В каждый конкретный лепесток, связанный с определенной базовой точкой, включаются объекты, для которых такая сумма минимальна. После данной операции все объекты будут распределены по лепесткам без учета вместимости транспортного средства.
Для того чтобы узнать загруженность лепестков, необходимо использовать procedure LoadPetal. Эта процедура аналогична Procedure DividePoint, только она работает с множеством точек в одном лепестке. С помощью procedaure MostInefficientPetal определяем наличие избытка веса в лепестке. Если есть избыток, то применяем procedure TransferPoint, которая перемещает объект из лепестка, в котором имеется избыток веса, в один из соседних. Точка, у которой вес совпадает по знаку с перевесом и расстояние, от которой до соседнего лепестка минимально, перемещается. Данная процедура применяется до тех пор, пока все лепестки не будут сбалансированы.
Таким образом, после выполнения всех вышеуказанных процедур получены сбалансированные маршруты. Далее в каждом лепестке выбирается оптимальный маршрут при помощи procedure OptimalPlan.
При оптимизации маршрутов можно воспользоваться практически любым классическим методом. Поскольку количество обслуживаемых точек в рамках одного маршрута будет значительно меньше, чем во всем множестве.
Таким образом, данный алгоритм экономит время пересчета, поскольку изначально определяются оптимальное количество маршрутов. Обслуживаемые объекты оптимально группируются по всем маршрутам, и для оптимизации обслуживания каждого маршрута применимы уже классические методы.
Литература:
1. Эйрих С.Н. Обзор различных видов задачи маршрутизации транспорта// NEW MAGENTA PAPERS, 2012 №1, с. 11 – 19;
2. Suthikarnnarunai N. A Sweep Algorithm for the Mix Fleet Vehicle Routing Problem// Proceedings of the International MultiConference of Engineers and Computer Scientists, 2008 № 2;
3. Laporte G. Classical Heuristics for the Vehicle Routing Problem / G. Laporte, F. Semet // Les Cahiers du GERAD, G98-54, Group for Research in Decision Analysis. Montreal, Canada, 1998;
4. Эйрих С.Н. Обзор методов решения задач маршрутизации транспорта// NEW MAGENTA PAPERS, 2012 №1, с. 22 – 29;
5. Gendreau M. Metaheuristics for the vehicle routing problem / M. Gendreau, G. Laporte, J.- Y. Potvin // Technical Report CRT-963, Centre de Recherche sur les Transports. Universit de Montral, jan 1994;
6. Пожидаев М. С. Алгоритмы решения задачи маршрутизации транспорта. : дис… канд. техн. наук. — Томск. 2010. — С. 57-101.
