К. ф.-м. н. Коршунов М. К.

ФГАУ ВПО Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Россия

Обучение студентов экономических специальностей применению нейронных сетей

К настоящему времени приложения подобного рода широко используются в экономике. В то же время изучение этих дисциплин в курсах информатики и информационных технологий остаётся чисто теоретическим.  Для этого есть существенные причины. Эти системы дороги, требуют участия команды специалистов, сложны для освоения и настройки. Поэтому в подавляющей части курсов раздел искусственный интеллект не сопровождается лабораторными работами.  Умений и навыков по важному разделу информатики не формируется.

Анализ показывает, наиболее реальный  путь освоения  для студентов не технических специальностей методов искусственного интеллекта является нейросетевые технологии.

Однако эта область включает в себя множество самых различных систем и методов. На наш взгляд разумно ограничиться разделами нейросетевых технологий, для которых есть математическая теория позволяющая выбрать конфигурацию сети или образцы решения конкретных задач.

Рассмотри графическую метафору практикума по нейронным сетям.

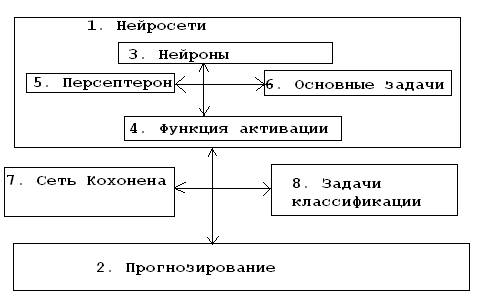
Рис. 1 Графическая метафора практикума

Теоретической основой практикума являются понятия искусственного интеллекта, нейронных сетей как одной из практических реализаций искусственного интеллекта.

Для решения задачи прогнозирование временного ряда необходимо уметь исследовать его характеристики. Это можно делать в Microsoft Excel [1,2]

Для практических целей необходимо ограничить класс используемых рядов.

Определение 1. Слабо стационарным временным рядом называется временной ряд, для которого существуют средние, дисперсии и ковариации, не зависящие от времени.

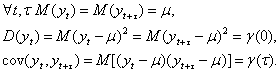
Напомним важные для прогнозирования характеристики временных рядов

Функция t-->g(t) называется автоковариационной функцией.

График автокорреляционной функции называется коррелограммой.

Для эмпирических оценок обычно принимается гипотеза эргодичности, позволяющая при оценивании значений автокорреляционной функции осреднение по реализациям заменить осреднением по времени.

Определение 3. Стационарный случайный процесс называется эргодическим, если среднее по множеству реализаций для заданных моментов времени равно среднему по времени, вычисленному по одной реализации.

Обычно постулируется эргодичность для выбранного отрезка временного ряда.

В эконометрических пакетах присутствует возможность построения графиков АКФ и ЧАКФ, на которых показаны выборочные оценки коэффициентов автокорреляции и частной автокорреляции в зависимости от значений лагов.

Выборочные оценки для стационарного эргодического временного ряда:

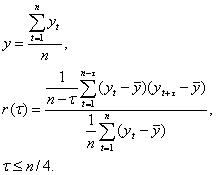
Определение 4. Частная автокорреляционная функция измеряет корреляцию между уровнями ряда 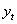 и

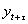, разделёнными t временными тактами, при исключении влияния на эту взаимосвязь всех промежуточных уровней ряда

.

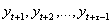Определение 5. Авторегрессионным временным рядом порядка р называется случайный временной ряд вида

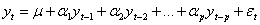
Параметры 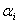называются коэффициентами авторегрессии,

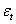 «белый шум».

Множество таких временных рядов обозначается как АR(p).

Многочлен 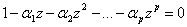 называется характеристическим многочленом временного ряда. Оно называется характеристическим потому, что его корни определяют характеристики временного ряда

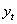
Предложение1. Временной ряд, задаваемый моделью авторегрессии, является стационарным тогда и только тогда, когда все корни его характеристического уравнения по модулю больше единицы.

Практические рекомендации по идентификации авторегрессионных моделей [1].

1 У моделей AR(p) значения коэффициентов АКФ экспоненциально затухают.

2. ЧАКФ для модели AR(p) имеет выбросы на первых р лагах, а значения коэффициентов для лагов, больших порядков, статистически незначимы.

Определение 6. Временной рядом скользящего среднего порядка q называется случайный временной ряд вида

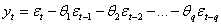
Параметры 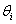называются коэффициентами,  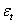«белый шум».

Множество таких временных рядов обозначается как MA(q).

Практические рекомендации по идентификации  моделей скользящего среднего[1].

1 АКФ для модели MA(q) имеет выбросы на первых q лагах, а значения коэффициентов для лагов, больших порядков, статистически незначимы.

2. У моделей MA(q)  значения коэффициентов ЧАКФ экспоненциально затухают.

Определение 7. Временным рядом авторегресии порядка р и скользящего среднего порядка q называется случайный временной ряд вида

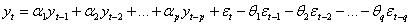
Параметры

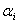называются коэффициентами авторегрессии,

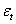 «белый шум».

Множество таких временных рядов обозначается как АRMA(p,q).

Определение 8. Пусть временной ряд после взятия последовательных разностей (после дифференцирования d-го порядка) становится стационарным, удовлетворяющим модели ARMA(p,q)

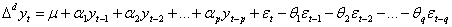
Тогда модель АRIMA(p,d,q) применима к исходному виду.

Выбор d может быть осуществлён визуально. Если график зависимости y от времени имеет ненулевой тренд или дисперсия y изменяется от времени, то переходят к анализу графика Dy и т.д.

Критерием правильности состоит в том, что коэффициент парной корреляции зависимой переменной с её лагированными значением статистически незначимо отличен от нуля для любого номер лага.

Формально, d это максимальное значение к, для которого АКФ 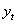 и

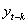 значимо отлично от нуля.

Для оценки p и q задаются начальные значения  p и q. Затем оцениваются коэффициенты уравнения

,

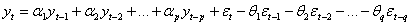Соответствующие заданным p и q . После этого тестируются остатки полученной модели на наличие автокорреляции. Остатки правильно специфицированной модели должны вести себя подобно белому шуму.

При расчёте предсказаний прогнозы выполняются последовательно, период за периодом. При этом в правой части уравнения модели коэффициенты заменяются их оценками, ошибки – остатками, и предполагается, что за пределами выборки ошибки равны нулю.

Специфицировав вероятностную модель можно построить нейросетевую модель этого ряда.

Далее необходимо освоить понятия и процедуры, связанные с использование нейронных сетей и работу с конкретным пакетом для решения этой задачи. Естественно для студенческого практикума необходим пакет, максимально автоматизирующий решение задачи, исключающий необходимость решения непринципиальных задач. 

Такими возможностями обладает пакет Deductor Studio, входящий в состав аналитической платформы Deductor Life. Свободная версия пакета позволяет решать задачи с ограничением 150 записей,  что вполне достаточно для студенческого практикума.

Исходные данные готовятся в электронных таблицах. Дальнейшая работа сводится к запуску мастера и ответу на его вопросы.

Все результаты выдаются в простой и наглядной форме. Продемонстрируем ключевые этапы решения практической задачи.

Исходные данные накапливаются  таблицах Excel.

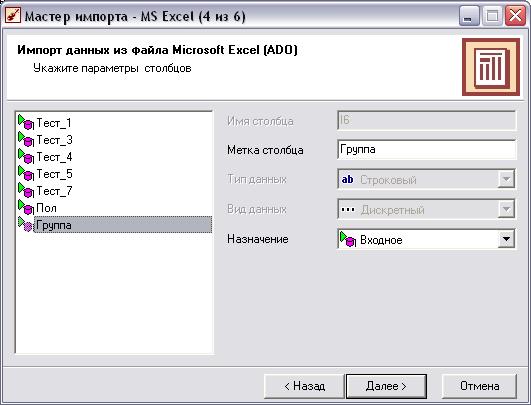
Настройка импорта данных (Рис.2)

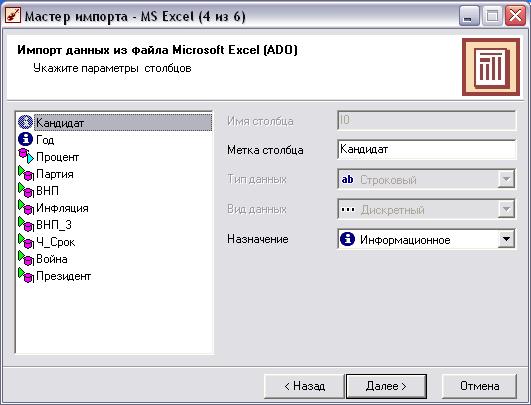
Рис 2 Настройка импорта данных

Задаём структуру сети (Рис.3)

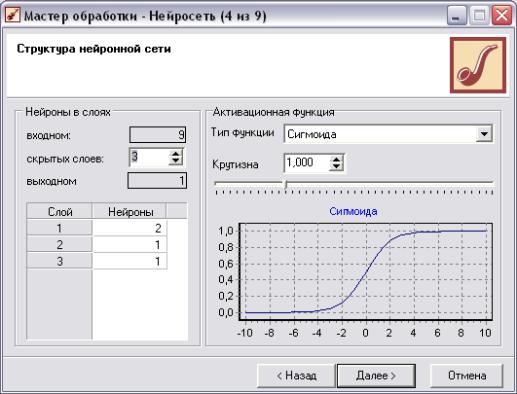
Рис. 3. Выбор типа сети

Результаты обработки (Рис.4)

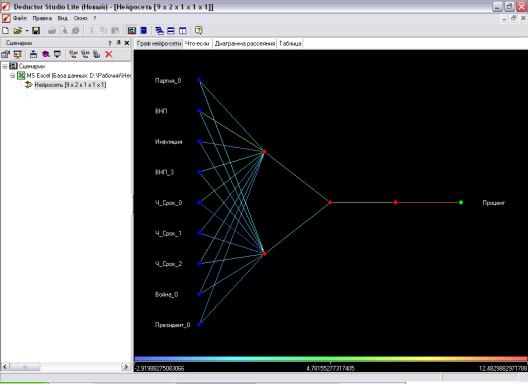
Рис 4 Построенная сеть

Построенная сеть используется для прогнозирования.

Аналогичным образом решается задача с сетью Кохонена. Эта сеть решает задачу классификации без образцов. Это естественные условия для многих задач.

Настройка параметров импорта

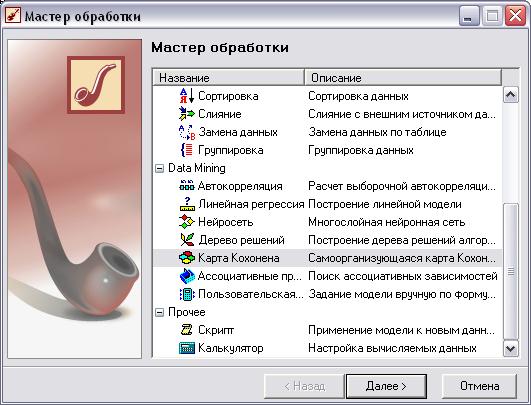
Запускаем мастер обработки

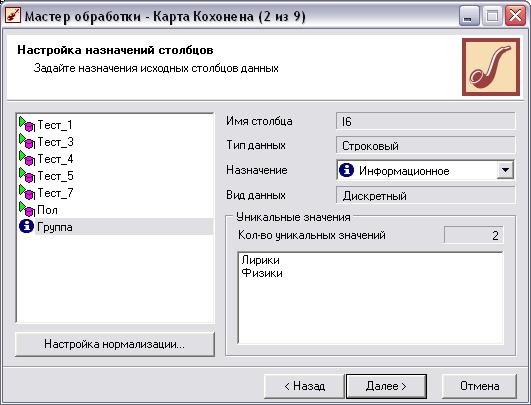
Настраиваем назначения столбцов

Настраиваем разбиение исходных данных

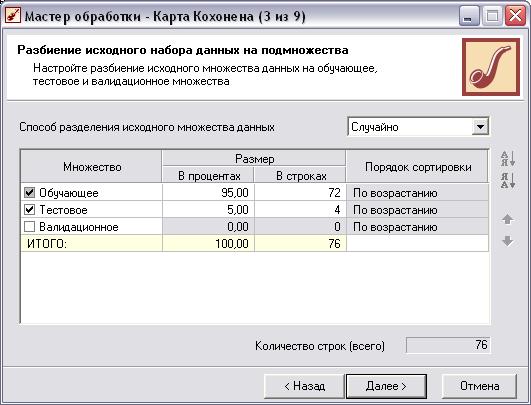
Настраиваем параметры карты Кохонена

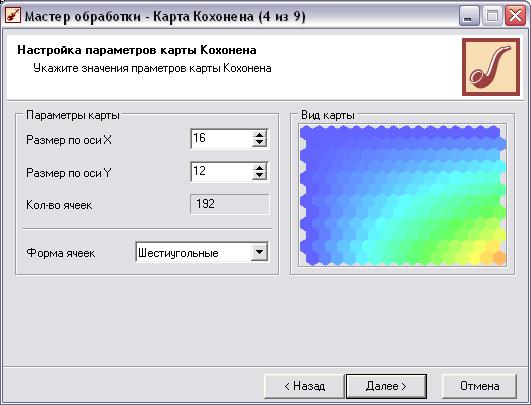
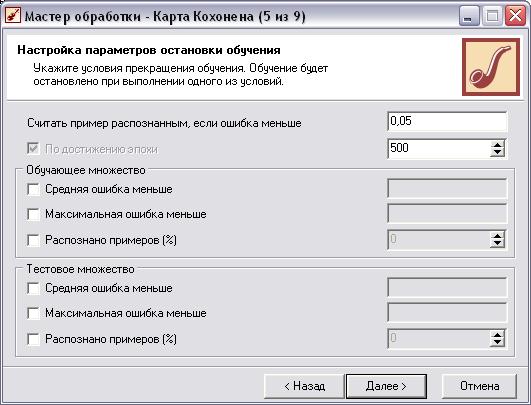
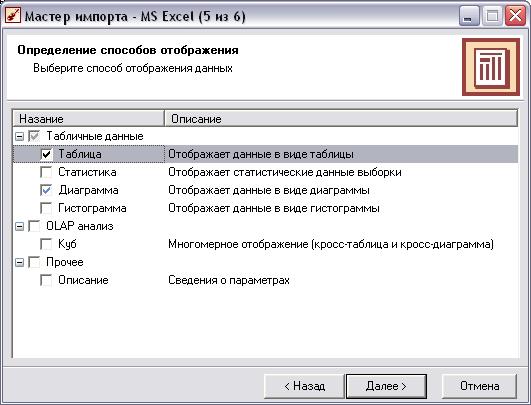
Настройка параметров отображения результатов

Таким образом, современные нейросетевые пакеты позволяют элиминировать несущественные технические операции и  обучить студентов экономических специальностей решению практически важных задач.

Результаты работы используются при выполнении курсовых работ студентами экономических специальностей

Литература

1. Бабешко Л,О. Математичексое моделирование финансовой деятельности-М.:КНОРУС, 2009.-224 с.

2. Дуброва Т.А. Прогнозирование социально-экономических процессов.-М.:Маркет ДС,20110.-192с.

3. Круглов В.В., Борисов В. В. Искусственные нейронные сети. Теория и практика.-М: Горячая линия Телеком, 2002

4. Таров Д.А. Нейронные сети –М.: Радиотехника, 2005

5. Аистов А,В. Эконометрика шаг за шагом-М.:ВШЭ, 2006-178 с

6. Эконометрика:практикум.-М.МГИМО,2010-145с.