Ковалева Е.Д., Жебит В.М.

Эконометрическая модель результативности модернизационных преобразований на примере региона республики Беларусь

ЭКОНОМЕТРИЧЕСКАЯ МОДЕЛЬ РЕЗУЛЬТАТИВНОСТИ

МОДЕРНИЗАЦИОННЫХ ПРЕОБРАЗОВАНИЙ НА ПРИМЕРЕ РЕГИОНА РЕСПУБЛИКИ БЕЛАРУСЬ

Определение потенциала экономического развития региона является одной из важнейших задач региональной экономики. Данный процесс во многом зависит от инвестиций, которые осуществляются в региональной хозяйственной системе. Для выявления тенденций модернизационных преобразований в Республике Беларусь на примере Минской области возможно применение эконометрических методов анализа.

Особый интерес представляет оценка влияния факторов на эффективность инвестиционных процессов в регионе.

Решение этой задачи требует определения результирующего показателя, характеризующего эффективность инвестиционных процессов. Здесь речь идет о процессах инвестирования средств в основной капитал.

Оценка эффективности инвестиционных процессов в регионе является актуальной проблемой. Уровень эффективности процессов инвестирования средств в основной капитал является интегральной характеристикой и определяется достаточно большим множеством факторов. Построение такого показателя в рамках детерминированных моделей затруднительно. Наш подход основан на применении линейной модели множественной факторной регрессии. Зависимой, обобщающей переменной мы предлагаем использовать объем инвестиций в основной капитал [1].

Многофакторная модель строится в соответствии с функциональной зависимостью типа:

Y –инвестиции в основной капитал, млрд.руб.;

х1 – уровень безработицы (%);

х2 – доля инвестиции в основной капитал организаций с участием иностранного капитала (%);

x3 – уровень экономической активности населения (%);

x4 – индекс промышленного производства (в % к предыдущему году);

x5 – удельный вес убыточных организаций (в % от общего числа организаций);

x7 – инвестиции в основной капитал на душу населения (тыс. руб.);

x8 – индекс физического объема инвестиций в основной капитал (в % к предыдущему году);

x9 – удельный вес инвестиций в основной капитал в валовом региональном продукте;

x10 – доля собственных средств в источниках финансирования инвестиций в основной капитал, %;

x11 – доля банковских кредитов в привлеченных источниках финансирования

инвестиций в основной капитал, %;

x12 – доля бюджетных средств в привлеченных источниках финансирования инвестиций в основной капитал, %;

e – случайная составляющая.

Исходная система данных рассчитана по Минской области за 2000–2012 гг. Значения признаков-показателей были отобраны на основе статистических сборников: «Регионы Республики Беларусь – 2005», «Регионы  Республики Беларусь – 2012», «Инвестиции в Республике Беларусь – 2005» «Инвестиции в Республике Беларусь – 2012» и данных Национального статистического комитета Республики Беларусь [2].

Обработка собранной аналитической информации проводится с помощью

корреляционного и регрессионного анализа. Корреляция характеризует меру зависимости переменных между собой.

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной. Информация о наличии такой связи может быть использована при анализе множественной регрессии, для построения регрессионного уравнения [3].

Описанный выше метод используется в исследовании для анализа корреляционной зависимости 12 факторов, предположительно влияющих на итоговый показатель – сальдированный финансовый результат в расчете на 1 руб. инвестиций в основной капитал.

Корреляционная матрица независимых факторных признаков показывает, что они слабо коррелируют между собой, и поэтому с применением метода пошаговой регрессии появляется возможность построить значимую модель линейной регрессии (см. табл. 1).

Таблица 1 – Корреляционная матрица независимых факторных признаков

Примечание – источник: собственная разработка на основании [4]

Для получения регрессионного уравнения необходимо провести ступенчатый отсев регрессоров. Процесс повторяется до тех пор, пока не останутся только значимые регрессоры.

В результате получено следующее уравнение множественной регрессии следующего вида:

Y = 1.407566726*X7 + 266.0806903*X9 + 17.17103391 (2)

Коэффициенты регрессионной модели на заданном уровне значимы.

Статистические оценки модели и ее параметров оказались полностью состоятельными (рис. 1):

Примечание – источник: собственная разработка на основании [4]

Обычной коэффициент детерминации равен R2= 0,999987, это означает, что изменение результирующего фактора инвестиций в основной капитал на 99.9 % зависит от изменения исследуемых независимых факторов, а на долю других факторов приходится 0.1 % изменений.

Исправленный коэффициент детерминации = 0,999984, он отличается от обычного на 0.000003. Данная разница не велика. Значение этих коэффициентов достаточно велики. Это значит, что регрессия аппроксимирует достаточно точно эмпирические данные.

О неслучайной природе полученных значений коэффициентов регрессии свидетельствуют их стандартные ошибки. В наших расчетах принят 5 %-й ( p = 0,05) уровень вероятности  ошибки. В модели расчетные значения стандартных ошибок для всех коэффициентов регрессии меньше задаваемого уровня. Из рис. 1 видно, что статистика критерия Фишера равна F= 384997,5.  Так как p=0,0000, что меньше, чем a = 0,05, то гипотеза о незначимости модели отклоняется.

Анализ остатков представлен на рисунке 2.

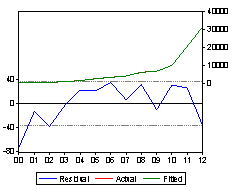
Рисунок 2 – Анализ  графика остатка

Примечание – источник: собственная разработка на основании [4]

Наблюдаются значительные колебания. В начале периода в 2000-2001 гг. значения остатков выходят за пределы доверительного интервала. С 2002 по 2006 гг. значения остатков возрастают, а после наблюдаются колебания со значительной амплитудой. Значение остатков не симметричны относительно оси Ох.

Адекватность модели – это соответствие реальному явлению. Т.е. необходимо что бы остатки удовлетворяли четырем условиям Гаусса-Маркова или четырем предпосылкам МНК.

Первое условие: математическое ожидание остатков равно 0.

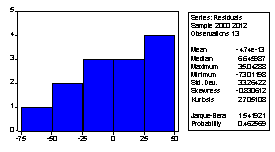
Примечание – источник: собственная разработка на основании [4]

Т.к. среднее =-4.74*10-13 то данное значение равно 0. Значит условие адекватности выполняется.

Второе условие: нормальный закон распределения остатков. Тест Жака Бера нулевая гипотеза остатки подчиняются нармальному закону распределения. Т.к. Р=0,462569 больше чем 0,05 то по эквивалентной форме критерия нулевая гипотеза отклоняется. Следовательно, условие адекватности выполняется.

Третье условие адекватности: дисперсия остатков постоянна. Тест Уайта

Примечание – источник: собственная разработка на основании [4]

Так как Р=0,144455 это больше 0.05, то по эквивалентной формуле нулевая гипотеза не отклоняется. Следовательно, дисперсия случайных ошибок в модели постоянна для всех наблюдений. Условие адекватности выполняется. Проверим принадлежность к процессу белого шума.

Примечание – источник: собственная разработка на основании [4]

Ряд является стационарным, т.к. Prob. меньше 0,05, нулевая гипотеза отклоняется.

Таким образом, полученное уравнение множественной регрессии (2) показывает высокую тесноту связи между эффективностью инвестиционных процессов в Минской области и выделенными приоритетными признаками-показателями. Об этом свидетельствуют высокое значение коэффициента множественной корреляции.

На основе проведенного факторного исследования динамики инвестиций в регион можно сформулировать следующие основные выводы по Минской области:

1. Уравнение линейной множественной регрессии (2), его аналитическое качество, подтверждаемое высоким значением коэффициента детерминации и исправленного коэффициента детерминации, а также отмеченные выше статистически состоятельные оценки параметров модели показывают, что эффективность процессов инвестирования средств в основной капитал в Минской области имеет высокую тесноту связи с выделенными приоритетными факторными признаками. Кроме того, на основе полученной регрессионной модели выявлен ряд важных тенденций в динамике инвестирования средств в Минской области.

2. На увеличение совокупной чистой прибыли предприятий и организаций Минской области  в результате инвестирования средств в основной капитал наибольшее положительное влияние оказывали следующие два фактора:

· инвестиции в основной капитал на душу населения (тыс. руб.);

· удельный вес инвестиций в основной капитал в валовом региональном продукте.

Литература:

1.Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL: Учебное пособие / Э. А. Вуколов. – М: ФОРУМ: ИНФРА-М, 2004. – С. 160.

2.Регионы Республики Беларусь. Социально-экономические показатели. 2012: Стат. сб. / Белстат. - Минск,2012. - 732 с.

3.Айвазян С.А., Бродский Б.Е. Макроэконометрическое моделирование: подходы, проблемы// Прикладная эконометрика. 2009. №2. С.85-111.

4.Янковский, И.А. Прикладная эконометрика: методические указания / И.А.Янковский.-Пинск: ПолесГУ ,2013.-44с.