Чурсинова Е.М., Чернейко А.В.

Построение регрессионной модели количества вновь выявленных онкологических заболеваний по Минской области за 2005 – 2011 гг

Полесский государственный университет, Беларусь, г. Пинск

Построение регрессионной модели  количества вновь выявленных онкологических заболеваний по Минской области за 2005 – 2011 гг.

Эффективность лечения больных злокачественными новообразованиями находится в прямой зависимости от своевременного выявления их на ранних стадиях заболевания, однако во всех странах мира существует проблема онкологической запущенности. Для анализа используется динамика онкологической запущенности за период 2005-2011 гг. в Минской области, где принимались меры по организации своевременного выявления онкологических заболеваний. Злокачественные новообразования (ЗНО) занимают одно из ведущих мест в структуре смертности населения многих стран мира.

В практику лечения онкологических заболеваний активно внедряются новые сложные и высокотехнологичные оперативные вмешательства, совершенствуются методики лучевой и химиотерапии. Но, по-прежнему, эффективность лечения больных злокачественными новообразованиями находится в прямой зависимости от своевременной диагностики их на ранних стадиях заболевания [1].

Проблема раннего выявления онкологических заболеваний является, в первую очередь, организационной проблемой [1], для решения которой необходимо четко знать причины, приводящие к развитию онкологической запущенности. Все случаи, когда злокачественное новообразование выявляется в далеко зашедшей стадии, подлежат тщательному анализу с целью установления причины несвоевременного выявления ЗНО.

Для анализа поставленной проблемы в работе был применен традиционный подход, основанный на использовании математических моделей. Так как математические модели позволяют решать широкий круг задач исследования: обнаружение и анализ статистических закономерностей в исследуемом временном ряде; построение на базе выявленных эмпирических экономических зависимостей эконометрической модели; проверка качества найденных параметров модели самой модели в целом;  использование построенных моделей для объяснения, прогнозирования и предсказания и поведения исследуемых экономических показателей [2].

Для построения регрессионной модели был применен пакет программ Eviews. Так как данный инструмент  лучше всего раскрывает возможности при решении задачи прогнозирования количественных показателей, представляющих собой именно временной ряд. Следует отметить, что в пакете Eviews имеется достаточный набор  методов по обнаружению и борьбе с типичными  проблемами: гетероскедастичность, автокорреляция, нестационарность и наличие коинтеграции [2].

При построении регрессионной модели количества вновь выявленных причин онкологических заболеваний в Минской области использовались годовые данные за период: с 2005 по 2011 годы. Можно выделить следующие потенциальные факторы [4]:

- Абсолютное число вновь выявленных онкологических заболеваний на 100, тыс. чел., количество случаев.

- Скрытое течение болезни, период.

-  Несвоевременное обращение, количество случаев.

-  Отказ от обследования, количество случаев.

-  Погрешности диспансеризации.

- Число специалистов на 100 тыс. населения, человек.

- Вредные выбросы в атмосферный воздух по Минской области, тыс. тонн.

- Неполное обследование, количество случаев

- Ошибки рентгенологической диагностики, количество случаев.

- Коэффициент  достоверности, единиц

В качестве эндогенной переменной выступает  абсолютное число вновь выявленных онкологических заболеваний в Минской области 100 тыс. населения. 

В качестве экзогенных переменных – оставшиеся перечисленные выше факторы.

При построении модели были введены обозначения исходных временных рядов. Условные обозначения временных рядов приведены в таблице 1.

Таблица 1 – Условные обозначения временных рядов

Учитывая требования отсутствия мультиколлиниарности (зависимость между факторами) факторов, при построении модели необходимо включать в нее минимальное количество факторов [2].

Для выявления наиболее значимых независимых переменных и возможной мультиколлинеарности были рассчитаны значения коэффициентов корреляции Пирсона ( Таблица 2).

Таблица 2. Матрица парных коэффициентов корреляции Пирсона

При этом высокие значения коэффициентов корреляции указывают на наиболее значимые независимые переменные.

Анализ матриц парных коэффициентов корреляции позволил выявить статистически значимые линейные корреляционные связи между исследуемыми переменными.Таким образом, для построения регрессионной модели в качестве независимой переменной используется переменная .

Перед непосредственным построением моделей и их анализом  на адекватность, необходимо проверить каждый временной ряд для определения его стационарности, а в случае нестационарности – для определения порядка интегрированности. От этого зависит построение по исследуемым  временным рядам регрессионной модели методом наименьших квадратов, без каких-либо преобразований. Это возможно в том случае, если все факторы представлены стационарными временными рядами или если временные ряды являются коинтегрированными.

На рисунках 1-2 отображены значения исследуемых временных рядов.

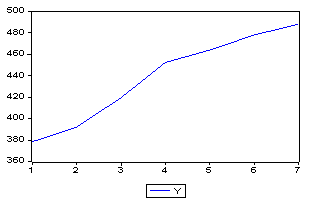
Рисунок 1. Временной ряд «Абсолютное число вновь выявленных онкологических заболеваний на 100, тыс. чел., количество случаев»

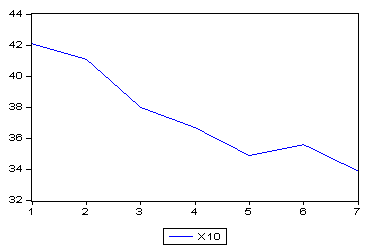
Рисунок 2. Временной ряд «Коэффициент  достоверности, единиц»

Для определения типа нестационарности и порядка интегрированности необходимо провести  три варианта теста Дики-Фуллера: со смещением, с трендом, без смещения и без тренда (процесс белого шума). Нулевая гипотеза состоит в том, что  конкретный временной ряд  нестационарен (имеет единичный корень). Результаты применения теста Дики-Фуллера для исследуемых временных рядов приведены в таблице 3.

Таблица 3. Результаты теста Дики-Фуллера

По результатам теста Дики-Фуллера можно заключить, что исходные временные ряд  являются нестационарным и временной ряд  стационарный.

С помощью метода наименьших квадратов была построена модель количества вновь выявленных онкологических заболеваний по Минской области за 2005 – 2011 гг.

(1) Y = -13.42036048*X10 + 941.994365

(2) t-значения  (0.0001) (0.0000)

(3) R2 =  0.958467,  0.950160, DW = 2.89, Prob(F-statistic) = 0.000121

Статистические показатели модели и тесты подтверждают ее приемлемое качество.  Анализ остатков не выявляет автокоррелированность (p-значение критерия множителя Лагранжа  равно 0.40), не обнаруживает гетероскедастичность (p – значение критерия Уайта равно 0.27), не выявляет значимого отклонения от нормального распределения ( P-значение критерия Жака – Берра равно  0.94).Построенная модель является адекватной. Данная модель может быть использована для анализа данных. Остатки построенной модели являются стационарными.

При анализе результатов медицинских исследований часто возникает необходимость определения достоверности полученных данных.

При увеличении значения фактора х10 на  единицу значение y уменьшится на 13,4 случая, так как коэффициент перед х10 меньше 0, то связь между изучаемыми переменными: с увеличением факторной переменной х10  на единицу результативная переменная y уменьшается на 13.4 случая.

1. Залуцкий, И.В. Совершенствование работы экспертных комиссий по раннему выявлению онкологических заболеваний / И.В.Залуцкий, Ф.Е.Венскевич // Здравоохранение. - 2011. - №7. - С.17-20.

2. Информационный портал по эконометрическому моделированию «Стратосфера» http://statosphere.ru/blog/34-compstatprog.html

3. Отчет Центральной экспертной комиссии по раннему выявлению онкологических заболеваний за 2006-2011 годы - [Электронный ресурс] - http://rnpcmt.belcmt.by/

4. Официальный сайт Республиканского научно-практического центра медицинских технологий, информатизации, управления и экономики здравоохранения, г. Минск - [Электронный ресурс] -http://rnpcmt.belcmt.by/