Тажин Ю.А.
Использование методов исследования операций для решения типовых задач обоснования управленческих решений (Часть 1)
независимый эксперт в области системно-финансового анализа,
экономических приложений Data Mining и Fuzzy-технологий
Использование методов исследования операций для решения
типовых задач обоснования управленческих решений
(Часть 1)
Важную роль в обосновании управленческих решений играют экономические расчёты, некоторые из которых (если, вообще не большинство!) можно свести к типовым задачам:
– исследования операций;
-->
По мнению автора, подтверждённому глубоким анализом источников, посвящённых финансовому менеджменту и специальным вопросам принятия управленческих решений, а также собственной практикой, здесь как, и в любой другой отрасли человеческой деятельности, весьма отчётливо просматривается закономерность, подмеченная ещё в XIX столетии итальянским учёным Вильфредо Парето: порядка 80% отмеченных задач являются типовыми и только около 20% – несводимыми к типовым. На эту закономерность, названную «правилом Парето» обращают внимание (в контексте анализа предпринимательских рисков) такие авторитетные отечественные исследователи проблем общего менеджмента, связанных с обоснованием управленческих решений, как С.Н. Воробьёв и К.В. Балдин /1, с.248-257/, а также В.С. Ефремов /3/ и О.И. Ларичев /4/.
Таким образом, сводимость к типовым задачам исследования операций значительного количества проблемных ситуаций, с которыми на практике сталкивается предприниматель (иное лицо принимающее решение – ЛПР или исследователь) является фундаментальным свойством исследуемых систем управления, а, значит, позволяет в большинстве случаев обоснованно формализовать и с нужной исследователю степенью точности решить практически важную хозяйственную задачу.
В философском аспекте это свойство отражает важный гносеологический аспект научной познаваемости социально-экономических систем, частным случаем которых являются хозяйственные системы (или бизнес-системы, расчленяемые с точки зрения системного анализа на совокупность органически взаимосвязанных бизнес-процессов).
Рассмотрим несколько типовых задач системного анализа, возникающих в практике обоснования принимаемых управленческих решений, обращая внимание как на формально-алгоритмическую сторону, так и на процесс абстрагирования исходных данных. О таком аспекте, как точность решения следует сказать отдельно.
Пока же сконцентрируем своё внимание на аспектах, как абстрагирование исходных данных и построение самого порядка (алгоритма) того или иного типового экономико-управленческого расчёта.
Графическим методом найти max и min функции F на множестве, задаваемом системой ограничений:
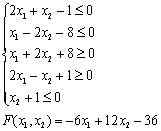
Комментарий автора статьи.
Такого рода задачи, относящиеся к классу задач линейного программирования относительно двух целевых переменных (ЛП-2), могут возникать на практике во множестве анализируемых хозяйственных ситуаций. Типичная хозяйственная ситуация – выбор оптимальной стратегии размещения заданного объёма финансовых ресурсов (например, кредитов юридическим и физическим лицам) в коммерческом банке, сопряжённой с нормативными ограничениями ЦБ РФ.
Рассмотрим алгоритм решения данной абстрагированной выше относительно исходных данных задачи. Он состоит из следующих этапов.
1 этап («Алгебраический»). Преобразуем систему ограничений, выразив х2 через х1:
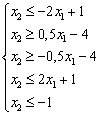
2. этап («Геометрический»). По двум точкам на декартовой плоскости построим прямые, соответствующие ограничениям-равенствам (рис.1).
В качестве характерных точек для каждой прямой выбираем точки пересечения осей х1 и х2, приравнивая в уравнениях соответствующих прямых к нулю х2 и х1 соответственно: 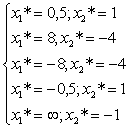
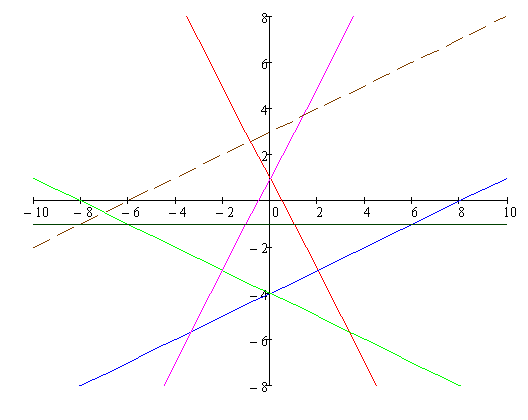
Рис.1. Иллюстрация «Геометрического» этапа решения задачи ЛП-2.
Этап 3. («Смешанный»). Пунктиром на рисунке 1 проведём прямую целевой функции:
F(x1,x2) = –6x1 + 12x2 – 36.
Множество, задаваемое системой ограничений, выделяем густой штриховкой (рис.2).
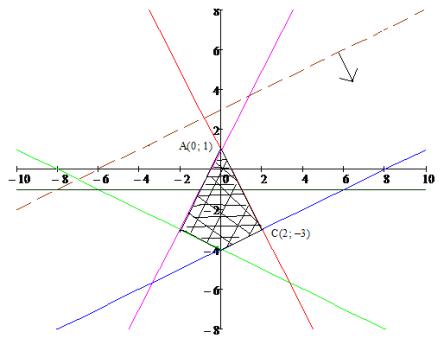
Рис.2. Иллюстрация «Смешанного» этапа решения задачи ЛП-2.
Максимум целевой функции достигается в точке А(0; 1) – первой точке пересечения «движущейся» в перпендикулярном к самой себе прямой целевой функции направлении с границей заштрихованной области, минимум – в точке С(2; –3) – крайней или последней точке пересечения указанных прямой и границы. Направление «движения» показано стрелкой на рис.2. Таким образом, находим минимальное и максимальное значения целевой функции.
![]()
Итак:
![]()
Решение задачи найдено. Теперь попробуем отвлечься от конкретных чисел и ответить на важный для системного аналитика вопрос: моделью какой типичной проблемной хозяйственной ситуации, сопряжённой с выбором оптимального решения может быть решённая задача?
Если немного подумать, что ответ напрашивается легко. Представим себе, что некий банк решил открыть кредитный филиал в регионе Х.
При этом известно, что на кредитование юридических лиц выделяется средний удельный объём финансовых ресурсов (в некоторых условных единицах, пропорциональных, например, среднему показателю финансово-операционной потребности /5/, приходящейся на одного условного заёмщика), описываемый переменной x1, а на кредитование физических лиц – x2 соответственно. Ожидаемый суммарный риск убытков описывается линейной целевой функцией F(x1,x2). Как получена эта функция – нам пока не важно. Но, забегая вперёд, можно сказать, что такого рода функция получается как регрессионная кривая (в данном случае – прямая) по данным внутренней статистики проблемных кредитов банка. Техника расчёта коэффициентов регрессионной кривой – предмет для построения отдельной математической модели.
Перед руководством филиала стоит задача: определить допустимые размеры лимитов ожидаемого убытка для одного кредита по каждому из двух видов заёмщиков («юрикам» и «физикам» – соответственно) с таким расчётом, чтобы этот лимит находился между некоторым минимальным и максимальным значениями, задаваемыми a priori руководством головного банка, как оптимальные резервы возможных потерь по ссудам (РВПС) исходя из нормативов ликвидности и доходности в соответствии с требованиями ЦБ РФ.
Анализируя полученное решение, исходя из такой постановки задачи, мы видим, что:
– во-первых, и постановка и решение задачи являются системной моделью довольно актуальной хозяйственной ситуации выбора в условиях риска и неопределённости;
– во-вторых, аналитические возможности построенной модели далеко не ограничиваются отмеченной выше хозяйственной ситуацией;
– в-третьих, построенная системная модель может служить общей системной моделью для построения алгоритма поддержки принятия решения в аналогичных хозяйственных ситуациях выбора в условиях риска, когда число выбираемых переменных равно двум, целевая функция – линейная, а ограничения выбора (также линейные), будучи представлены прямыми декартовой плоскости, пересекаясь, образуют выпуклую границу.
В заключение следует отметить, что более сложная и «многомерная» (по числу переменных) хозяйственная ситуация, системно аналогичная рассмотренной, сводится к типовой задаче линейного программирования вида ЛП-N, алгоритм решения которой известен под названием симплекс-метода /2, с.276-287/.
Библиография
- Воробьёв С.Н., Балдин К.В. Управление рисками в предпринимательстве. – М.: ИТК «Дашков и К0», 2006. – 772 с. ISBN 5-94798-553-0.
- Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.1. – М.: Высшая школа, 1997. – с. 304 с. ISBN 5-06-0037070-9.
- Ефремов В.С. Стратегия бизнеса. Концепции и методы планирования. – М.: Финпресс, 1998. – 192 с. ISBN 5-8001-0014-4.
- Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах. – М.: Логос, 2002. – 392 с. ISBN 5-94010-180-1.
- Любушин Н.П., Лещёва В.Б., Дьякова В.Г. Анализ финансово-экономической деятельности предприятия. – М.: Юнити, 2002. – 471 с. ISBN 5-238-00105-3.
