Мамонтов И.Ю.

Контейнерная площадка как одноканальная система массового обслуживания

« Container terminal as single-channel system of mass service»

Mamontov Ilya Jurevich, the post-graduate student of chair «Logistical transport systems and technologies» the Moscow State University of Railway Engineers  (MIIT) on a speciality 05.22.08"Management of processes of transportations»

· Контейнерная площадка

·  Теория массового обслуживания

·  Перегрузочные средства

·  Канал обслуживания

·  Случайная величина

·  Theory of mass service

· Reloading means

· Service channel

· Random variable

Аннотация: В данной статье представлено теоретическое описание контейнерной площадки, как одноканальной системы массового обслуживания.

The summary: The theoretical description of a container terminal is presented in this article, as single-channel system of mass service.

На основании изложенного каждую контейнерную площадку на терминале можно представить в виде системы, в которую поступает поток контейнеров на переработку (погрузки в вагон или автомобиль, а также выгрузку из вагона или автомобиля). Указанная переработка контейнеров производится либо козловыми кранами, либо специальными автопогрузчиками (ричстакерами).

Исследование функционирования таких систем может быть осуществлено методами теории массового обслуживания. Исследовательская модель представляет собой, в общем случае, систему массового обслуживания, которая характеризуется двумя параметрами: параметром входящего потока заявок на обслуживание и параметром обслуживания. Тот и другой параметры являются случайными в зависимости от закона распределения и структуры самой системы исследования и параметров ее функционирования.

Теория массового обслуживания имеет дело со случайными величинами, которые в значительной мере присутствуют и в работе любой контейнерной площадки. Так, например, случайной является масса груза в контейнере, поднимаемом козловым краном или автопогрузчиком. Поскольку заранее рассчитать массу загруженного отправителем контейнера не представляется возможным. Данный показатель, безусловно, зависит от внутренних размеров поданного под загрузку  крупнотоннажного контейнера, но и в этих пределах может значительно меняться, поскольку разные грузы отличаются объемом и способом транспортировки. Неопределенным заранее остается и тип контейнера, который понадобится грузоотправителю, будет это 20-фут. или 40-фут. контейнер остается неизвестным до момента подачи заявки на загрузку контейнера.

Помимо этого, случайным является время прибытия или завоза контейнеров на терминал. Просчитать даты окончания формирования и отправления со станции того или иного поезда, а соответственно и дату прибытия на терминал станции назначения очень сложно. Исключение составляют жесткие нитки графика контейнерных поездов, но далеко не весь график движения грузовых поездов состоит из подобных ниток.

Дата сдачи поезда на погрузку или разгрузку зависит от того насколько быстро на станции отправления будет сформирован поезд установленной длины из необходимого количества контейнеров, предъявленных отправителем к перевозке. Процесс прибытия груженых контейнеров от грузоотправителей на станцию имеет случайный характер в силу того, что зависит от целого ряда факторов. В том числе от даты заключения торговых контрактов, готовности груза к отправке, наличия товара на складе покупателя, от сезонности перевозок, а на морских терминалах еще и от погоды в портах отправления и назначения, оказывающей непосредственное влияние на подход судна и работу порта.

Аналогично работе железнодорожного транспорта и завоз груженых контейнеров автотранспортом на терминал не подлежит точному расчету из-за невозможности просчитать дату загрузки контейнера каждым конкретным отправителем. По мере готовности груза к отправке, отправитель заказывает необходимый контейнер у собственника последнего или нанимает экспедитора, который организует данную перевозку. Но сама дата отправки, в любом случае остается случайной.

В дополнении к вышесказанному, на каждой контейнерной площадке имеются все содержательные моменты моделей, описываемых теорией массового обслуживания, такие как: источник заявок на обслуживание, входящий поток требований, канал обслуживания, очередь в ожидании процесса обслуживания, простой канала обслуживания в ожидании поступления заявки на обслуживание.

Под источником заявок на обслуживание на площадке предлагается понимать  совокупность контейнеров, загруженных, например, в вагон или поступающих по завозу автомобильным транспортом на контейнерную площадку, которые по определенной процедуре необходимо выгрузить на площадку, или загрузить в подвижной состав автомобильного или железнодорожного транспорта.

Под каналом обслуживания на контейнерной площадке следует понимать устройства, выполняющие определенную технологическую операцию. Прежде всего, это погрузочно-разгрузочные средства для выгрузки контейнеров или погрузки их в подвижной состав автомобильного или железнодорожного транспорта.

К каналам обслуживания также относится подвижной состав автомобильного или железнодорожного транспорта, с помощью которого осуществляется такой вид обслуживания как доставка контейнеров. Количество каналов может изменяться от одного до некоторого конечного значения.

Работа любой контейнерной площадки состоит в переработке поступающего на него потока контейнеров или заявок. В нашем случае понятия контейнер и заявка тождественны. Контейнеры поступают один за другим в некоторые, случайные, моменты времени. Обслуживание поступившего контейнера продолжается какое-то время, после чего канал освобождается и снова готов для приема следующей заявки.

В том случае, если входящий поток является пуассоновским, а параметр обслуживания подчиняется экспоненциальному распределению, то система может быть исследована аналитическими методами. Данные методы теории массового обслуживания позволяют установить показатели эффективности системы массового обслуживания, описывающими с той или другой точки зрения ее способность справляться с потоком заявок (среднее число заявок, обслуживаемых в единицу времени; среднее число занятых обслуживанием каналов; средняя длина очереди и среднее время ожидания каждой заявкой начала обслуживания и др.).

В том случае, если параметр обслуживания подчиняется закону распределения отличному от экспоненциального, то система может быть исследована аналитическими методами, если она является одноканальной системой массового обслуживания. В соответствии с этим необходимо провести качественный и количественный анализ параметров потока заявок и параметра обслуживания. В остальных случаях система массового обслуживания может быть исследована численными методами (методы математического моделирования).

В значительной мере подход аналитического и численного моделирования случайных процессов в методическом плане основан на трудах отечественных ученых, таких как Н.П. Бусленко, Е.С. Вентцель [2], Б.В. Гнеденко [3], А.В. Горелик [4], и других, а также на трудах зарубежных авторов, таких как А. Кофман [5], Р. Крюон, Т. Саати.

Предметом теории массового обслуживания является установление зависимости между характером потока заявок, производительностью отдельного канала, числом каналов и эффективностью обслуживания.

В качестве характеристик эффективности обслуживания, в зависимости от условий задачи и целей исследования, могут применяться различные величины и функции. Например, среднее время простоя отдельных каналов и системы в целом; среднее время ожидания в очереди; вероятность того, что поступившая заявка немедленно будет принята к обслуживанию; закон распределения длины очереди и т.д.

Каждая из этих характеристик описывает, с той или другой стороны, степень приспособленности системы к выполнению потока заявок, иными словами – ее пропускную способность.

Пропускная способность, в общем случае,  зависит не только от параметров системы, но и от характера потока заявок. Например, на контейнерной площадке моменты поступления контейнеров случайны, как и длительность обслуживания заявки. В связи с этим процесс работы площадки протекает нерегулярно: в потоке контейнеров образуются места максимума и минимума. Первое может привести к образованию очередей. Второе к непроизводительным простоям технических средств или подвижного состава, а также площадки. На эти случайности, связанные с неоднородностью потока заявок, накладываются еще случайности, связанные с задержками обслуживания отдельных контейнеров.

Таким образом, процесс функционирования контейнерной площадки, как системы массового обслуживания, представляет собой случайный процесс. Данный процесс, протекающий в системе массового обслуживания, состоит в том, что система в случайные моменты времени переходит из одного состояния в другое: меняется занятость канала обслуживания, число заявок, стоящих в очереди и т.п.

Поэтому, чтобы дать рекомендации по рациональной организации системы, выяснить ее пропускную способность и предъявить к ней требования, необходимо изучить случайный процесс, протекающий в системе, и описать его математически.  Для описания случайных процессов, происходящих в системе контейнерной площадки и непосредственно связанных с работой технического комплекса каждой площадки, в настоящей работе предложен математический аппарат теории массового обслуживания.

В теории массового обслуживания существуют так называемые, одноканальные и многоканальные системы. В работе контейнерной площадки, как было сказано выше, под каналом обслуживания можно понимать погрузочно-разгрузочные средства, предназначенные для переработки контейнеров.

При этом площадка, как правило, оснащена несколькими кранами и погрузчиками с различными техническими характеристиками. На практике все имеющиеся на площадке перегрузочные средства будут отличаться друг от друга по ряду признаков: грузоподъемности, режиму работы, сроку службы, способу передвижения захватного устройства, скорости подъема груза  и т.д. Данное обстоятельство говорит о том, что на площадке вновь поступивший контейнер может быть переработан любым из имеющихся в наличии погрузочно-разгрузочных средств с определенными техническими характеристиками машины.

Таким образом, необходим качественный анализ обслуживания технического комплекса площадки, который определяется как параметром каждого технического средства, так и системы их.

Поэтому для анализа эффективности технического комплекса контейнерной площадки не всегда имеет смысл рассматривать последний, как многоканальную систему обслуживания. Достаточно дать комплексную оценку техническому оснащению площадки, учитывая особенности каждого погрузочно-разгрузочного средства. 

В соответствии с этим в настоящей работе принято решение представить все  погрузочно-разгрузочные машины, работающие  на контейнерной площадке, независимо от их количества не как несколько параллельных  каналов с разными параметрами обслуживания, а как один комплекс, характеризуемый суммарным параметром обслуживания. Это, по предварительной оценке  должно существенно упростить методику и процедуру исследования параметров функционирования контейнерного терминального комплекса.

Именно такой подход аналитического исследования функционирования   контейнерного терминального комплекса в виде одноканальной системы массового обслуживания выносится на защиту в данной диссертационной работе.

Наличие общего для всей системы параметра производительности определяется техническими особенностями каждой погрузочно-разгрузочной машины.

На основании вышеизложенного рассмотрим контейнерную площадку, как одноканальную систему массового обслуживания с входящим потоком заявок, который подчиняется закону Пуассона. Последнее означает, что поступающие в систему заявки образуют, так называемый, простейший поток, который обладает тремя основными свойствами: ординарностью, стационарностью и отсутствием последействия.

Ординарность потока означает практическую невозможность одновременного поступления двух и более заявок (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени).

Стационарным называют поток, для которого математическое ожидание числа заявок, поступающих в систему в единицу времени, не меняется во времени. Это значит, что число заявок, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным.

Отсутствие последействия обусловливает взаимную независимость поступления того или иного числа заявок на обслуживание в непересекающиеся промежутки времени. Это означает, что число заявок, поступающих в данный отрезок времени, не зависит от числа заявок, обслуженных в предыдущем промежутке времени.

На практике условия простейшего потока не всегда строго выполняются. Часто имеет место не стационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца).

Кроме того, количество поступающих на площадку контейнеров увеличивается на число контейнеров, требующих переработки внутри самой площадки.

Например, обслуживающие площадку технические средства должны переработать не только входящий поток контейнеров, поступивших по завозу автотранспортом, но и погрузить или выгрузить контейнеры, предназначенные к отправке или прибывшие железнодорожным транспортом. В дополнении к вышесказанному имеет место внутренняя сортировка контейнеров, выполняемая на площадке погрузочно-разгрузочными машинами. Примером такой сортировки может служить перестановка имеющихся на площадке контейнеров, обусловленная определенной необходимостью. В общем виде схема контейнерной площадки как одноканальной системы массового обслуживания представлена на рис. 1.

Анализ работы контейнерной площадки с точки зрения рассмотрения последней как одноканальной системы массового обслуживания предложен  автором работы впервые. При этом все погрузочно-разгрузочные машины, составляющие технический комплекс площадки, объединены в один канал обслуживания. Условно принято, что контейнер, поступивший в систему, может с равной вероятностью быть переработан любым из имеющихся в наличии кранов или автопогрузчиков. Данный подход позволит применить к описанию работы контейнерной площадки аналитические методы теории массового обслуживания. Последние предлагаются автором как математический аппарат для определения эффективности функционирования технического комплекса контейнерной площадки.

Список литературы:

1. Белый О.В., Попов С.А., Францев Р.Э. Транспортные сети России (системный анализ, управление, перспективы), СПб.: СПГУВК, 1999, 147с

2. Вентцель, Е.С. Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель,  Л.А. Овчаров.  – 3-е изд., перераб. и доп.  – М.: Издательский центр «Академия», 2003. – 432 с.

3. Гнеденко, Б.В. Математические методы в теории надежности / Б.В. Гнеденко. – М.: Наука, 1965. – 522 с.

4. Горелик А.В. Исследование операций / А.В. Горелик, И.А. Ушаков.  – М.: Машиностроение, 1986. – 288 с.

5. Кофман, А. Массовое обслуживание. Теория и приложение / А. Кофман, Р. Крюон. – М.: Мир, 1965. – 302 с.

6. Кузнецов, А.П. Методологические основы управления грузовыми перевозками в транспортных системах / А.П. Кузнецов. – М.: ВИНИТИ РАН, 2002. – 274 с.

7. Матюшин, Л.Н. Контейнерные и контрейлерные перевозки грузов: Справочник. Часть 3 / Л.Н. Матюшин, П.В. Баскаков. - М.: Интеграция, 2009. – 287 с.

8. Резер, С.М. Проблемы управления транспортом и логистики / С.М. Резер. – М.: ВИНИТИ РАН, 2008. – 512 с.

Сведения об авторах:

Мамонтов Илья Юрьевич, аспирант кафедры «Логистические транспортные системы и технологии» МГУПС (МИИТ) по специальности 05.22.08 «Управление процессами перевозок», ведущий инженер сектора отдела продаж по перевозкам с участием Японии и Кореи компании ОАО «ТрансКонтейнер». Тел. 8-916 249 9742 (моб.), 8 (495) 788 17 17 доб. 1193 (сл.). E-mail: ilya-mamontov@mail.ru

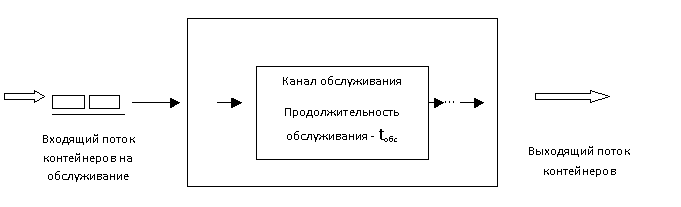
Рис. 1. Контейнерная площадка как одноканальная система массового обслуживания.