Стрельцова Е.Д., Богомягкова И.В., Стрельцов В.С.

Модель поддержки принятия решений на базе алгоритма равновесия по Нэшу

В [1] изложены результаты создания автоматной модели, функционирующей в переключаемых случайных средах и используемой для принятия решений при бюджетном регулировании. Переключаемые случайные среды описываются автором вероятностными характеристиками поступлений бюджетных средств от уплаты налогов различных видов, участвующих в долевом распределении , где оценка вероятности выигрыша автомата   в случайной среде действия поступлений от уплаты налога ,  номера состояний автомата . В связи с тем, что долевое распределение средств от уплаты налогов должно обеспечить достижение некоторого компромисса между уровнями бюджетной системы, авторами предлагается модель игрового поведения двух систем «автомат-переключаемая среда» как инструмента логического согласования интересов бюджетов вышестоящего и нижестоящего уровней бюджетной системы РФ. Рассмотрим формальное описание этой игры.  Игра  в нормальной форме описывается тройкой , где – множество индексов, отражающих количество игроков, в роли которых выступают системы  и ; ,  – декартово произведение стратегий, доступных игрокам  и ;  множество индексов, отражающих количество номеров состояний автоматов;  множество номеров переключаемых случайных сред автоматов;  – стратегия, доступная игроку , ; ,  – случайная среда, в которой функционирует автомат; количество состояний автомата;  количество случайных сред системы «автомат-переключаемая среда»;  набор функций выигрышей игроков  и  соответственно. Если обозначить множество выигрышей переменной  , то функции выигрышей ,  можно представить как отображения , , ставящие в соответствие каждому набору  стратегий  выигрыш этого игрока . Вследствие того, что множества игроков  и стратегий  конечны (мощности этих множеств составляют соответственно , , ), игра  формально описывается в виде матрицы . Элементами матрицы являются числа , , представляющие собой соответственно выигрыши игроков  и  в стратегиях  , , . В качестве выигрыша игрока  при наборе стратегий   примем вероятность выигрыша системы «автомат-переключаемая среда», величина которой  определяется в соответствии с аналитическими выражениями:

, если .

Выигрыш игрока,  имеющий вид , обозначим переменной : .

Решение игры в  ищется в  форме смешанных стратегий.  Для этого на множестве чистых стратегий , доступных игрокам   и , зададим вероятностное распределение , ставящее в соответствие каждой чистой стратегии  игрока ,  вероятность , . Это вероятность того, что стратегия  будет играться игроком , причём выполняется условие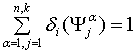. Тогда будем иметь пространство наборов смешанных стратегий , где ,  – набор смешанных стратегий игрока . Носителем смешанной стратегии является множество чистых стратегий , которым приписана положительная вероятность. Будем рассматривать смешанное расширение  игры , где  множество чистых стратегий, которые игрок   играет с положительными вероятностями в ситуации

, , а игрок   играет с положительными вероятностями  в ситуации

, .

Смешанные стратегии игроков  и  будем искать исходя из условия равновесия по Нэшу в смешанном расширении , в соответствии с которым при заданном распределении вероятностей противника ожидаемый выигрыш от применения чистых стратегий одинакова при любой стратегии противника.

Только в данном случае при нахождении смешанных стратегий необходимо учесть тот факт, что игрок  знает свою функцию выигрыша  , но не знает функции выигрыша игрока . То есть возникает задача описания ситуации с неполной информацией, когда игрок  сталкивается с некоторой неопределённостью относительно выбора стратегии игроком . В этой ситуации выдвинем следующую гипотезу. Примем, что выигрыш  игрока  при выборе стратегии , ,  распределён равномерно на отрезке . Правомерность этого предположения можно обосновать тем, что  финансовые управления вышестоящего уровня бюджетной системы РФ ЛПР в виду их заинтересованности в экономическом развитии всей территории и в зависимости от характера решаемых в данный период задач могут с равной вероятностью считать  своим выигрышем тот выигрыш, который получен при управлении бюджетной системой нижестоящего уровня. Игрок  будет играть свою стратегию , если его выигрыш  от этой стратегии будет не меньше некоторого заданного числа , т.е. если . Вероятность этого условия может быть определена следующим образом: . Очевидно, что вероятность выполнения условия  определяется из выражения

;  .

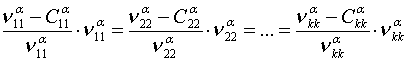Из последнего выражения получим следующую систему уравнений:

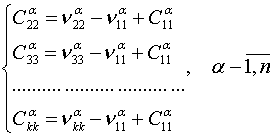 . (1)

Из системы уравнений (1) определяется значения

,

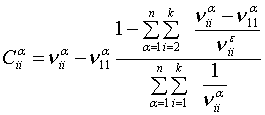или с учётом выражения  :

.

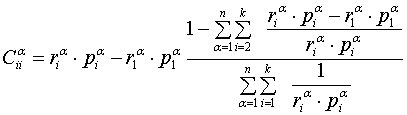Величины  позволяют определить вероятностное распределение , ; .  чистых стратегий игрока . Смешанные стратегии используются как коэффициенты для определения нормативов отчислений  в бюджет нижестоящего уровня бюджетной системы РФ по налогу вида   по формулам 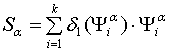. Выражения для положены в основу алгоритмов определения величин процентных отчислений от уплаты налогов в порядке бюджетного регулирования, приведённые в следующем разделе диссертационной работы.

Литература

1. Богомягкова И.В. Модель долевого распределения налогов в системе поддержки принятия решений по управлению межбюджетным регулированием //Научные ведомости Белгородского государственного университета (серия Информатика).-2010.-Выпуск 13/1