Срумова Ф.В.

Об асимптотике энергии для решения линейной системы уравнений Максвелла

Вычислена асимптотика энергии, излученной в пространство почти периодическим источником электромагнитных волн.

Рассмотрим следующую начально-краевую задачу для линейной системы уравнений Максвелла первого порядка

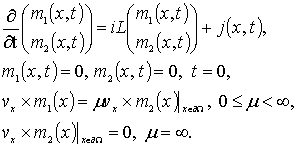(1)

Здесь  - нормаль,  и   - соответственно электрические и магнитные поля;  -трёхмерные векторные функции   соответственно, 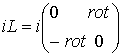 - самосопряжённый эллиптический оператор первого порядка, действующий в , где - открытая область в , содержащая внешность некоторой  сферы, причём граница области   принадлежит классу   . Пусть 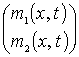 - классическое решение задачи (1). Вопрос о существовании и единственности такого решения исследован в работе [1]. Энергией  назовем интеграл

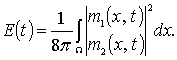
Следуя методу работы [2], вычислим асимптотику функции  при  для обобщённого решения задачи (1). Как известно [3], обобщённое решение задачи (1) существует и единственно. Обозначим в дальнейшем   ядро спектральной функции самосопряжённого оператора 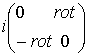 , которое представимо в следующем виде:

,

где -матрица решения задачи рассеяния [4].

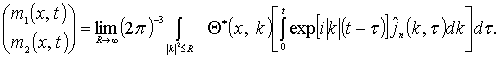(2)

Здесь

Интеграл (2) сходится в .

Лемма 2. Справедливо равенство

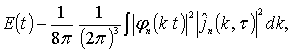
где

Рассмотрим далее функции

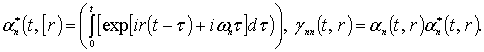
В результате вычислений получим

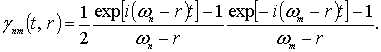
Лемма 3. Пусть  тогда

(4)

Пусть  -точка Лебега функции , тогда

. (5)

Доказательство. При условии, что величина   ограничена по  и  в окрестности  и

,

находим (4). Используя теорему о ядрах типа Фейера и соотношение

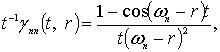(6)

имеем (5).

Пусть

(7)

Теорема. Если

1) ,

2)  для всех  и  есть точка Лебега функции  , то

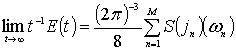. (8)

Доказательство. Если учесть (7), то (3) приобретает  вид

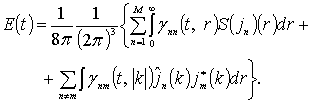
Принимая во внимание лемму 3, получим (8).

Литература

1. Schmidt G.- Arch. Rational Mech. and Anal., 1968, v. 28, N 4. p. 284-322.

2. Арсеньев А.А.- ЖВМ и МФ, 1970, т. 10, №4.

3. Ладыженская О.А.- Мат. сб., 1956, т. 39, вып. 4.

4. Пыжьянов А.М. –Дифференц. уравнения, 1974, т.10, № 6.