Алабугин А.А., Алюков С.В., Топузов Н.К.

Математическое моделирование систем управления ресурсосбережением предприятия

Многомерность статистических данных, присущая сложным социально-экономическим системам, определяет актуальность задач построения группировок и классификаций. При отсутствии обучающих выборок и априорной информации о характере распределения наблюдений растет неопределенность задач разбиения на классы, называемые в этом случае кластерами.

В тоже время, для повышения объективности оценок влияющих факторов в экспертных нечетких базах данных о социально-экономических системах необходимы содержательные управленческие и экономические числовые параметры взаимоотношений объектов. Действительно, при использовании разных модификаций метода взвешенной суммы частных технико-экономических показателей неявно предполагается, что при недостатке одних показателей можно их компенсировать избытком других. Однако, часто сравнению подвергаются предприятия, показатели которых отличаются в несколько раз (фактор неоднородности данных). При таком разбросе показателей чувствительность  результирующих показателей не может быть постоянной на всем факторном пространстве.

На величину интегрального показателя результативности влияют не только статистически оцениваемые количественные показатели, но и степень инновационности потенциала предприятия, персонала, его мотивированности, прочие социальные, экономические факторы и условия, часто плохо поддающиеся непосредственной количественной оценке. Для оценки таких показателей зачастую применяются экспертные вербальные оценки типа: «нерациональное использование ресурсов», «отличный уровень подготовки персонала», «высокий командных дух». Такая неопределенность исходных данных связана с невозможностью проведения дорогих полномасштабных исследований, а также с ограниченным доступом к правдивой финансовой и иной отчетности конкурентов.

В указанных условиях с помощью традиционных подходов трудно получать адекватные экономико-математические модели управления для оценки, например, инновационно-ресурсного потенциала предприятия и планирования его использования. В этих случаях широко применяются методы, учитывающие доступные экспертные знания. Понятно, что такие оценки имеют некоторую степень субъективизма и очевидно размытые границы. Превращать разные экспертные правила в математическую модель удобно с помощью теории нечетких множеств [2].

На наш взгляд целесообразно осуществить процесс интеграции различных инструментов количественного и качественного анализа в единый алгоритм, который позволит использовать преимущества существующих методов и уменьшить их недостатки. Применение количественных методов вероятностной оценки влияния факторов на результативные показатели можно оценить на основе регрессионных зависимостей. Использование таких зависимостей позволит снизить субъективность логических оценок влияния показателей-факторов на прогнозируемое поведение объектов. Кроме того, это дает возможность экспертам более обоснованно скорректировать оценки под воздействием полученных результатов. Взвешенные показатели-факторы в инструментарии нечётких множеств корректируются методами оценки рисков и граничных значений вероятностей качественных характеристик.

Критерием, например, качества или эффективности управления, инновационности или конкурентоспособности предприятия назовём число  Чем больше значение этого критерия, тем выше устойчивость развития предприятия, его инвестиционная привлекательность. На подобные результирующие показатели влияет многие производственные, социальные, экономические и другие характеристики. Обозначим их через . Тогда интегральный показатель результативности функционирования систем будет представлять функциональное отображение вида: , где  – вектор влияющих характеристик.

При большом числе характеристик их влияние удобно классифицировать в виде иерархического дерева логического вида (рис. 1).

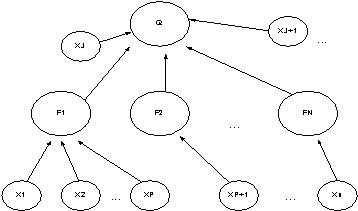
Значения факторов будем выражать как отклонения от усредненных показателей по аналогичным  факторам сравниваемых предприятий. Для моделирования укрупненных влияющих факторов используются экспертные нечеткие базы знаний типа Мамдани [2], приведенные в табл. 1.

Таблица 1 – Нечеткая база знаний для моделирования показателя результативности функционирования систем

Для некоторых факторов количество независимых характеристик может быть значительным. Правила отображения нечетких значений характеристик в нечеткие значения таких факторов могут быть громоздкими, что затрудняет процедуру сравнительной оценки вариантов развития предприятий. Поэтому при проведении такой оценки нами предлагается комбинировать методы нечеткого моделирования с широко известными методами статистической обработки данных, такими, как регрессионный анализ, факторный анализ, многомерное шкалирование. Так, методами факторного анализа и главных компонент можно значительно сократить число исходных характеристик, используя характеристики-заменители, либо латентные переменные. Уменьшение числа исходных характеристик позволит значительно упростить формирование свода правил.

Разрабатываемый нами интегративный метод предлагается включить в общий инструментарий экономико-математического моделирования развития сложных систем. Для этого следует учесть особенности оценки их результирующих (зависимых) и объясняющих (предикторных) переменных. Часть из них не поддается непосредственному измерению. Кроме того, исследователю и эксперту, нередко неясна степень тесноты статистической связи между анализируемыми переменными. Поэтому целесообразна следующая методика применения интегративного метода:

1. Предрегрессионный анализ многомерной общей совокупности данных (методами корреляционного анализа выбирается и оценивается измеритель статистической связи, проверяется гипотеза о её значимости). Например, устанавливается это по отношению к показателям уровней инновационности, адаптивности, производительности труда, ресурсосбережения как целевых, или зависимых переменных и качества управления факторов производительности труда, как объясняющих переменных.

2. При выявлении измеримости показателей входа и выхода модели стандартными методами находятся уравнения регрессионной связи [1]. В случае невозможности непосредственного измерения рассматриваемых свойств сложной системы решается задача оценивания сводного показателя F (Х) с точностью до произвольного монотонного преобразования. Содержательная (экономико-управленческая) интерпретация целевой функции при достаточной однородности исследуемых объектов либо (функцией управления качеством развития) их параметров и ограниченности времени, применения модели может быть представлена аппроксимацией линейного вида в виде разложения в ряд Тейлора либо индексно-факторной модели.

3. Организация обучения и опроса экспертов для балльной оценки выходных оценок результирующих показателей Fi.

4. Статистическая оценка объясняющих переменных Хj, дополняемая при необходимости экспертными балльными оценками статистических неизмеряемых показателей.

5. Построение искомой целевой функции  с количественными оценками Fi и Xj.

6. Количественное определение элементов антецедентов нечетких правил в баллах или долях единицы для замены нечетких словесных показателей в табл.1 в целях многовариантного прогнозирования или более глубокого анализа. При этом можно для соизмерения результатов, рекомендовать известные в практике вербально-числовые шкалы: очень высокая оценка показателя – 0,80…1,00; высокая – 0,64…0,80; средняя – 0,37…0,64; низкая – 0,30…0,37; очень низкая – 0,00…0,20. Достоверность указанных утверждений можно показать на примере моделирования влияния факторов на уровень эффективности использования персонала, который можно оценить коэффициентом отношения производительности труда к средней заработной плате.

Предложенные методы имеют универсальный характер. Поэтому их можно использовать не только для описания экономических и социальных процессов, как правило, имеющих высокую степень неопределенности, но и для решения значительно более детерминированных технических задач. Постановка технических задач также часто имеет субъективный характер. Например, при разработке моделей технических систем мы можем учитывать или не принимать во внимание зазоры в системе, упругость звеньев, трение в кинематических парах и т.п. субъективность постановки таких задач создает предпосылки  для совершенствования нечеткого моделирования.

Реализация п.6 предполагаемого нами интегративного метода разбиения области значений переменных на интервалы для выявления интервалов с низкими, средними и высокими значениями. При этом возможный нелинейный характер переменных часто затрудняет построение разбиений на равные интервалы. Непосредственное использование опыта и интуиции эксперта в таких ситуациях часто бывает достаточно рискованным с точки зрения хорошей сходимости экспертной оценки и реальности результатов. Для повышения точности экспертных оценок необходим дополнительный математический инструмент, помогающий экспертам в назначении диапазонов значений исследуемых переменных.

Для пояснения, рассмотрим, например, зависимость между экономичность автомобиля (оценивается в милях пробега на галлон расхода топлива) и мощностью двигателя (л.с.). исходные данные  для 403 автомобилей были собраны американской компанией SPSS Inc. и используются в данной статье с разрешения компании. Понятно, что экономичность автомобиля во многом определяется мощностью двигателя, типом используемой трансмиссией и другими характеристиками.

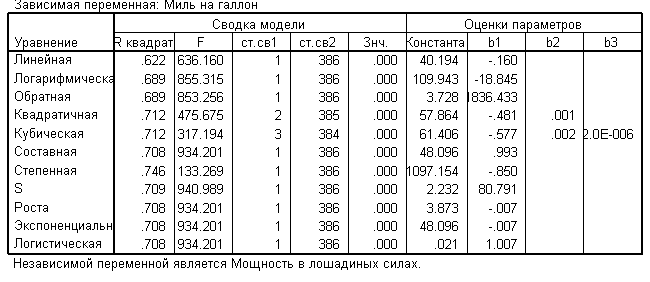
Регрессионный анализ, проведенный с помощью опции «подгонка кривых», позволяет подобрать наиболее подходящую зависимость для описания исходных данных. Как следует, наиболее высокий коэффициент детерминации (0,746) имеет степенная функция (табл. 2).

Таблица 2 – Сводка модели и оценки параметров

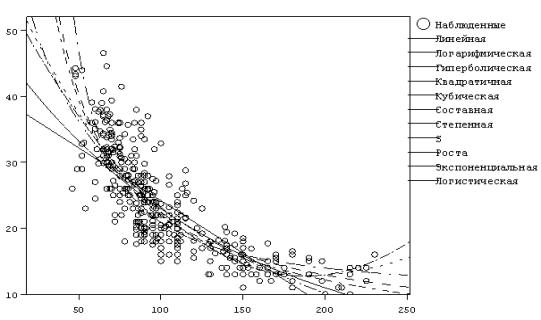
На рис. 2 изображены графики различных функций из данного набора, с помощью которых мы пытаемся наилучшим образом построить регрессионную модель.

Наилучшая регрессионная зависимость является и имеет вид , где независимая переменная х представляет собой мощность (л.с.), зависимая переменная y – экономичность автомобиля (миль на галлон). График функции изображен на рис. 3 использовать линейную зависимость не представляется рациональным, так как разность значений коэффициентов детерминации для степенной функции и линейной составляет 0,124 (см. табл. 2) и представляет собой достаточно большую величину.

Покажем, как назначить интервалы низких, средних и высоких значений для переменных «эффективность автомобиля» (миль на галлон) и «мощность» (л.с.) с учетом ярко выраженного характера нелинейности.

Для исходных данных ,  для точек А и В зададимся соответственно  координатами  и . Длину дуги АВ найдем с помощью криволинейного интеграла первого рода:

где .

Миль пробега на галлон расхода топлива

Мощность в лошадиных силах

Рис.2. Результат выполнения команды «подгонка кривых»

Находя производную регрессионной функции и подставляя в выражение (1), получим:

Интеграл (2) не берется в элементарных функциях в конечном виде, поэтому для его отыскивания воспользуемся разложением стандартной подынтегральной функции в ряд Маклорена с точностью до шестого порядка аппроксимации:

Подставив в формулу (3) вместо х выражение 869707,135(х-46)-3,70, получим разложение подыинтегральной функции в интеграле (2) в виде суммы степенных функций, допускающих дальнейшее интегрирование.

Миль пробега на галлон расхода топлива

Мощность в лошадиных силах

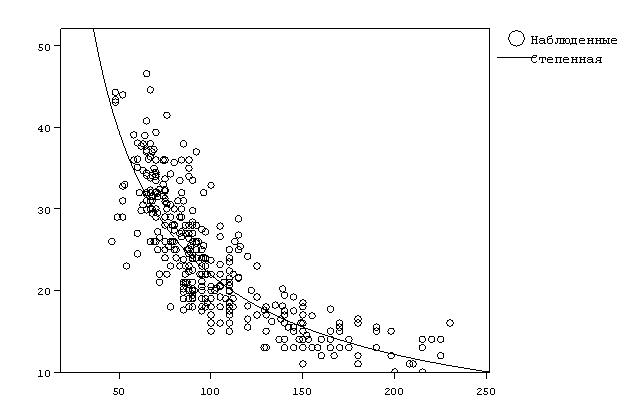
Рис. 3. График степенной регрессионной кривой, наилучшим образом

описывающей исходные данные

Предложенный путь возможен, но приводит к громоздким преобразованиям, поэтому воспользуемся программой MathCad Professional для приближенного нахождения интеграла (2). Тогда получим:

Развивая длину дуги на три части, получим промежутки кривой, соответствующие низким, средним и высоким значениям рассматриваемых переменных. Затем, зная длины этих частей, с помощью криволинейного интеграла  найдем середины  полученных частей дуги АВ. В нашем случае абсциссы этих середин с точностью до целых равны  ординаты центров найдем с помощью регрессионной функции у=1097,154х-0,850. При этом получим:  миль на галлон,  миль на галлон,  миль на галлон.

Как видим, если для переменной «мощность» расстояния между центрами достаточно близким по своим значениям, то для переменной «экономичность автомобиля» расстояния между центрами участков с низким, средним и высокими значениями переменной отличаются значительно в силу наличия нелинейности. Полученные результаты можно применить в дальнейших исследованиях с построением нечетких моделей.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Айвазян, С. А., Мхитарян В.С. Прикладная статистика и основы эконометрики: учеб. для экон. специальностей вузов / высш. шк. экономики (гос. Ун-т) М. : ЮНИТИ , 1998. – 1056 с.

2. Ким, Дж.-О, Мьюллер, Ч.У., Клекка, У.Р., Олдендерфер, М.С., Блешфилд, Р.К. Факторный, дискриминантный и кластерный анализ: Пер. с англ./ Дж.-О. Ким, Ч.У. Мьюллер, У.Р. Клекка и др.; Под ред. И.С. Енюкова. – М.: Финансы и статистика, 1989. – 215 с.
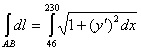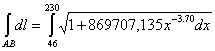