Калацкая Н.А., Пунько Ю.Г., Базака Л.Н.

Применение корреляционно-регрессионного анализа для получения прогноза по основным показателям предприятия

Полесский государственный университет

Применение корреляционно-регрессионного анализа для получения прогноза по основным показателям предприятия

Прогнозирование является важным этапом в процессе управления предприятием. Его результаты используются для выявления наиболее предпочтительных изменений, ожидаемых  в будущем состоянии предприятия, а также путей их достижения. От эффективных прогнозов зависит результативность работы предприятия в целом.

Использование различных специальных методов обработки, оснащенных пакетами программ машинной обработки статистической информации, таких как регрессионный и корреляционный анализы, гарантирует получение всестороннего и глубокого анализа информации (статистических данных по предприятию) [3].

Рассмотрены показатели предприятия ОАО ˮБерезовский сыродельный комбинат“. При построении регрессионной модели необходимо включать те факторы, которые описывают прибыль предприятия. На прибыль (результативный признак) оказывает влияние несколько потенциальных факторов: объем производства, цена, себестоимость продукции [2]. Учитывая требование отсутствия мультиколлинеарности (зависимость между факторами) факторов, при построении модели необходимо включать в нее минимальное количество факторов [4].

При проведении корреляционно-регрессионного анализа принято использовать следующий порядок действий: построение корреляционной диаграммы, построение модели линейной регрессии, расчет параметров модели, проверка модели на адекватность.

Для получения стабильного результата при построении регрессионных моделей необходимо проверить требование однородности исходной информации. Эта информация должна быть обработана на предмет аномальных, т.е. резко выделяющихся из массива данных, наблюдений. Эта процедура выполняется за счет количественной оценки однородности совокупности по какому-либо одномерному или многомерному критерию (в зависимости от исходной информации), целью которой является выяснение, у каких переменных наилучшие (или наихудшее) условия функционирования по не зависящим или слабо зависящим причинам [3] .

Также для того чтобы установить взаимосвязь между факторами можно использовать корреляционную диаграмму (диаграмму рассеивания) – это графическое представление статистического отношения между двумя или несколькими изменяющимися факторами [3].

Теснота (сила) связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции представляют собой количественную характеристику тесноты связи между факторами признаками (факторами), дают возможность определить ˮполезность“ факторных признаков при построении уравнений множественной регрессии. Величина коэффициентов корреляции служит также оценкой соответствия уравнению регрессии выявленным причинно-следственным связям.

Соответственно, корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. Различают: парная, частная и множественная.

Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными). Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков. Множественная корреляция – зависимость двух или более факторных признаков, включенных в исследование.

Термины корреляция и регрессия тесно связаны между собой. Первый термин оценивает силу (тесноту) статистической связи,  а второй исследует ее форму. Корреляция служит для установления соотношений между явлениями и для определения наличия или отсутствия связи между ними. Регрессия позволяет установить зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких [3].

Перед построением регрессионной модели необходимо произвести визуальный анализ значений результирующего признака для установление формы зависимости. Затем производят расчет значений параметров  модели в случае линейной регрессии с помощью метода наименьших квадратов. Использование этого метода обоснованно предположением о гауссовском распределении случайной переменной.

Для проверки гипотезы о значимости уравнения в целом используют F-статистику Фишера. Фактическое  значение  F -критерия  Фишера  сравнивается  с табличным (пороговым) значением F табл.  при заданном уровне значимости α и степенях свободы k1=m и k2=n-m-1.  При  этом,  если  фактическое значение  F-критерия  больше  табличного Fфакт > Fтеор, то  признается статистическая  значимость уравнения в целом на заданном уровне. Проверить  значимость  уравнения  регрессии  –  значит  установить, соответствует ли  математическая  модель,  выражающая  зависимость между переменными,  экспериментальным  данным  и  достаточно  ли включенных в уравнение  объясняющих  переменных (одной или нескольких)  для  описания зависимой переменной.

Также необходимо произвести оценку коэффициентов детерминации: обычного и исправленного (нормированного). Коэффициент детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи.  Коэффициент детерминации (обычный, R2 - обозначение) принимает значения в диапазоне от нуля до единицы. Коэффициент детерминации показывает, какая часть дисперсии результативного признака  объяснена уравнением регрессии. Чем больше R2, тем большая часть дисперсии результативного признака объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между результирующим признаком и объясняющий признаком коэффициент детерминации R2 будет близок к нулю. Таким образом, коэффициент детерминации R2 может применяться для оценки качества (точности) уравнения регрессии [3].

Корреляционный и регрессионный анализ, как правило, проводится для ограниченной по объёму совокупности. Поэтому показатели регрессии и корреляции – параметры уравнения регрессии, коэффициент корреляции и коэффициент детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить  адекватность построенных статистических моделей.

Для практического использования регрессионных моделей большое значение имеет соответствие фактических данных статистическим (адекватность модели) [1] – проверка четырех предпосылок МНК.

При анализе адекватности уравнения регрессии (модели) исследуемому процессу, возможны три варианта результатов.  Первый - построенная модель на основе F-критерия Фишера в целом адекватна и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов. Второй - модель по F-критерию Фишера адекватна, но часть коэффициентов  не значима. Модель пригодна для принятия некоторых решений, но не для прогнозов. Третий -  модель по F-критерию адекватна, но все коэффициенты регрессии не значимы. Модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы.

Чтобы  иметь  общее  суждение  о  качестве  модели,  из  относительных отклонений  по  каждому  наблюдению  определяют  среднюю  ошибку аппроксимации (1). Проверка адекватности уравнения регрессии (модели) осуществляется с помощью средней ошибки аппроксимации, величина которой  не должна превышать 10-12% (рекомендовано) [3].

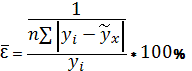
(1)

Где:   – фактическое значение результативного фактора;

 –  теоретическое значение результативного фактора;

– число наблюдений.

Рассмотренная методология корреляционно-регрессионного анализа и его основных параметров позволяет получить достаточно обширную аналитическую информацию. Корреляционный и регрессионный анализ позволяют определить зависимость между факторами, а так же проследить влияние задействованных факторов. Эти показатели имеют широкое применение в обработке статистических данных для получения прогнозных значений прибыли предприятия. Коэффициенты перед переменными означают, что при росте (снижении) значения соответствующей переменной на одну единицу измерения результирующий фактор изменится (увеличится, уменьшится) на значение соответствующего коэффициента. Так как количество наблюдений очень мало, то построение регрессионной модели нецелесообразно.

Литература:

1) Янковский И.А., Прикладная эконометрика: методические указания / И.А. Янковский. – Пинск: ПолесГУ,  2013.

2) Бухгалтерский отчёт предприятия ОАО ”Березовский сыродельный комбинат “ Елисеева И.И., Эконометрика: учебник для вузов / И.И. Елисеева. - М.: Финансы и статистика, 2002.

3) Колемаев В.А. Эконометрика: учебник / В.А. Колемаев. - М.: ИНФРА-М, 2006.