Серкебаева Л.Т.

Технология решения оптимизационых задач в Microsoft Excel

Костанайский государственный университет имени А.Байтурсынова, Республика  Казахстан

Технология решения оптимизационных задач

в Microsoft Excel.

При решении задач, возникающих в экономике, часто встает вопрос о выборе наилучшего в некотором смысле варианта решения. Иначе говоря, требуется решить задачу оптимизации, которая состоит в необходимости выбора наилучшего варианта решений среди некоторого, как правило, ограниченного множества возможных вариантов.

Оптимизация может быть достигнута только при постановке математического моделирования всех экономических и социальных систем. Задача оптимизации может быть сформулирована на языке математики, если множество доступных вариантов удается описать с помощью математических соотношений (равенств, неравенств, уравнений), а каждое решение - оценить количественно с помощью некоторого показателя, называемого критерием оптимальности или целевой функцией. Тогда наилучшим решением будет то, которое доставляет целевой функции наибольшее или наименьшее значение, в зависимости от содержательного смысла задачи.

- имеется единственная цель, функционально связанная с другими параметрами системы, которую нужно оптимизировать;

- имеются ограничения, выражающиеся, как правило, в виде неравенств;

Параметры задач ограничиваются такими предельными показателями:

- количество неизвестных - 200;

- количество формульных ограничений на неизвестные – 100;

- количество предельных условий на неизвестные - 400.

Алгоритм поиска оптимальных решений включает в себя несколько этапов:

- подготовительные работы;

- анализ решения.

Последовательность необходимых подготовительных работ, выполняемых при решении задач экономико-математического моделирования с помощью MS Excel приведена на рисунке 1.

Рисунок 1. Схема подготовительных работ

Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33 единиц питательного вещества А, 23 единиц вещества В и 12 единиц вещества С. Для откорма используется 3 вида кормов. Данные о содержании питательных веществ и стоимости весовой единицы каждого корма даны в таблице 1.

Таблица 1

Требуется составить наиболее дешёвый рацион, при котором каждое животное получило бы необходимые количества питательных веществ А,В,С.

Внесение исходных данных в электронную таблицу для последующего решения с использованием надстройки «Поиск решения» можно оформить следующим образом. (см. рисунок 2)

Командой меню Данные – Поиск решения вызывается окно «Поиск решения», которое заполняется для рассматриваемой задачи так, как показано на рисунке 3.

По получения оптимального решения проводится его анализ по полученным отчетам. Анализ устойчивости – изучение влияния изменений отдельно взятых параметров модели на  показатели оптимального решения. Анализ пределов – анализ допустимых изменений в оптимальном плане, при котором план остается оптимальным.

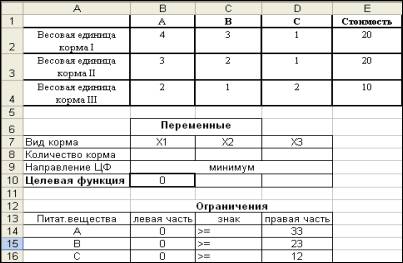
Рисунок 2. Оформление исходных данных в среде MS Excel

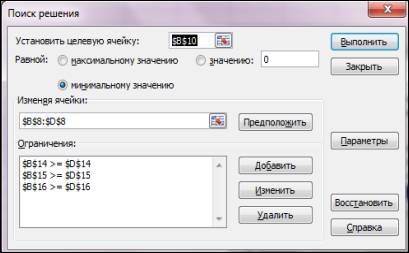
Рисунок 3. Заполнение диалогового окна «Поиск решения»

Анализ оптимального решения, встроенный в программу, представляет собой заключительный этап математического моделирования экономических процессов. он позволяет осуществить более глубокую проверку соответствия модели процессу, а также надежности оптимального решения. Основывается на данных оптимального решения и отчетов, которые выдаются в «Поиске решения». Но он не исключает и не заменяет традиционного анализа плана с экономических позиций перед принятием управленческого решения.

Литература:

1. В.Н.Пакулин. Решение задач оптимизации управления в MS Excel 2010

2. Тарасенко Н.В., Шеломенцева Н.Н. Математика-2. Решение задач оптимизации в Excel: Метод. указ. для студентов экономических специальностей. – Иркутск: Изд-во БГУЭП, 2003. – 43с.