Крылов В.Е.

Пространственно - временные диаграммы как способ моделирования социально - экономических систем

Владимирский Государственный Университет

имени Александра Григорьевича и Николая Григорьевича Столетовых

Пространственно – временные диаграммы как способ моделирования социально - экономических систем

Под социально – экономической системой мы понимаем взаимосвязанное множество социальных и экономических субъектов, а также отношений между ними, обусловленных распределением, потреблением материальных и нематериальных ресурсов, производством, распределением, обменом и потреблением товаров и услуг.

На существование и функционирование системы оказывают влияние всевозможные факторы, которые мы будем обозначать символами, ,…, . Рассмотрим интегрированный показатель S, являющийся функцией от факторов системы,

. (1)

Очевидно, что каждый фактор зависит от времени

Поэтому

. (2)

Значению времени соответствует значение функции (2)

.

Его мы будем называть состоянием системы.

Если состояние системы не зависит от времени, то система есть статическая, в противном случае – динамическая.

. (3)

Управление осуществляется в соответствие с некоторым планом – стратегией управления системой по переводу из одного состояния в другое.

С каждым управлением связан определенный критерий эффективности

. (4)

Соответственно, оптимальному значению критерия (4) соответствует оптимальное управление , а ему в свою очередь – оптимальная стратегия.

Очень удобным представляется моделирование управления с помощью пространственно – временных диаграмм (ПВД).

Рассмотрим декартову систему координат. По оси абсцисс будем откладывать значения функции S (1), а по оси ординат – время. Тогда состоянию системы  в данный момент времени  будет соответствовать точка А с координатами  (рисунок 1).

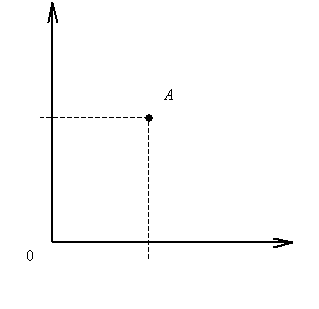
Рис. 1. Модель состояния системы.

Управление моделируется в виде направленной линии. Началу линии соответствует некоторое начальное состояние системы, а концу – конечное. В простейшем случае линия представляет собой луч. На рисунке 2 представлена ПВД, на которой процесс перехода системы из одного состояния в другое представлен в виде луча.

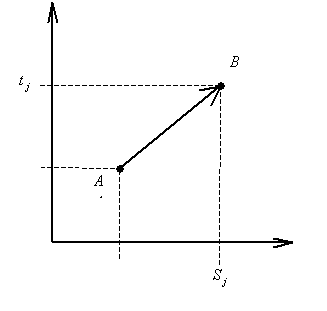
Рис. 2. Модель динамической системы.

Из рисунка 2 следует, что состояние системы меняется со временем. Значит, мы имеем дело с динамической системой. Исходя из определения, получаем: статической системе соответствует ПВД, изображенная на рисунке 3.

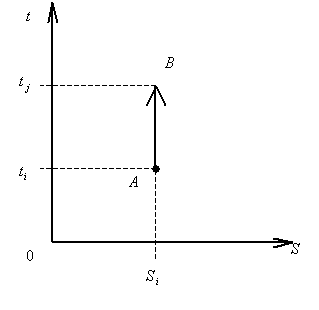
Рис. 3. Модель статической системы.

Ясно, что управление, помимо направления изменения процесса, характеризуется скоростью  и ускорением . Эти параметры находятся путем дифференцирования функции (1) по времени t:

, .

Пространственно – временные диаграммы позволяют по построенной модели управления определить и скорость и ускорение изменения состояния системы. На рисунке 4 представлена ПВД системы изменение состояния которой происходит с положительной скоростью, при этом оно замедляется со времени (система «прогрессирует» с «замедлением»).

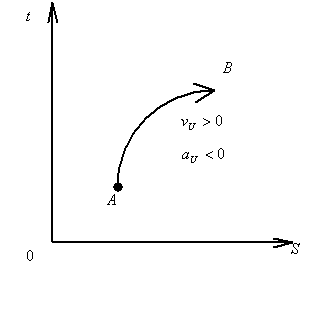
Рис. 4. Система «прогрессирует» с «замедлением».

Более подробно правила построения ПВД изложены в монографии [1] и статье [2].

В качестве примера применения ПВД приведем алгоритм построения оптимальной стратегии перевода социально – экономической системы из начального состояния в конечное (см. статью [2]).

1. Определяем ранние сроки  и поздние сроки  перевода системы в конечное состояние. Также находим конечные состояния системы, находящиеся в диапазоне от  до . Получаем многоугольник конечных состояний системы. Строим его на пространственно – временной диаграмме.

2. Разбиваем временной интервал, необходимый на перевод системы из начального состояния в конечное, на N частичных временных отрезка . Напомним, что в общем случае они могут иметь разную длину. Удобно, если длина отрезка разбиения кратна

.

3. Строим траекторию крайнего оптимизма. Затем на пространственно – временной диаграмме строим траекторию крайнего пессимизма. Тем самым, находим поле стратегий.

4. На каждом шаге в зависимости от выбранного значения коэффициента оптимизма  строим траекторию, соответствующую оптимальному управлению  на данном промежуточном шаге.

Пусть

- число, не меньшее нуля, но не большее единицы. Назовем его коэффициентом оптимизма. Оно характеризует степень риска, соответствующую i – тому состоянию системы. Значение коэффициента оптимизма определяет экспериментатор в зависимости от создавшейся ситуации и от субъективного его отношения к риску.

Тогда, оптимальному управлению, приводящему систему из состояния  в  соответствует траектория, построенная исходя из соотношения:

. (5)

Заметим, что если , то конец траектории пересечется с траекторией крайнего пессимизма в точке . Если же , то траектория в точке  пересечется с траекторией крайнего оптимизма.

Рассмотрим пример (рисунок 5). Пусть в момент времени   было решено, что значение коэффициента оптимизма можно принять равным

.

Применяя критерий (5) для времени  находим точку В:

.

Соединяем направленным отрезком точки А и В. Итак, оптимальному управлению , переводящему систему из состояния  в , соответствует направленный отрезок АВ.

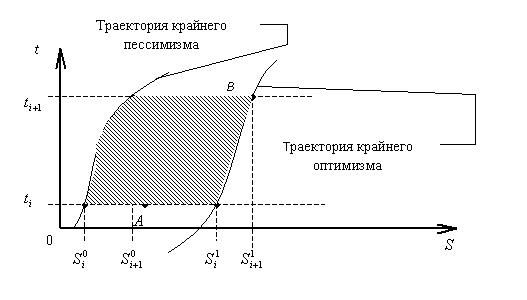
Рис. 5. Построение оптимального управления .

Неоспоримым преимуществом  критерия (5) является то, что со временем можно изменить значение коэффициента оптимизма исходя из сложившейся ситуации.

5. Объединяя вместе полученные в пункте 4 алгоритма управления , получаем оптимальное управление  для всей задачи:

.

6. По величине скорости изменения промежуточного состояния системы, соответствующей управлению , находим значение  критерия  эффективности применения стратегии. Тогда, суммарный эффект от применения оптимального управления, равен

ПВД, соответствующая алгоритму, представлена на рисунке 6.

Применение ПВД оказалось очень эффективным для моделирования развития муниципальных образований. Первые подходы к решению этой задачи осуществляются вместе в А.Ю. Андриановым [3]. Оказалось, что пространственно - временные диаграммы позволяют выстраивать стратегию развития муниципальных образований, производить прогноз возможных последствий.

Практика показывает, что пространственно - временные диаграммы являются очень удобным инструментом моделирования управления. Используя простейший математический аппарат, ПВД позволяют снимать параметры системы, строить прогноз ее развития, моделировать случаи взаимодействия социально – экономических систем.

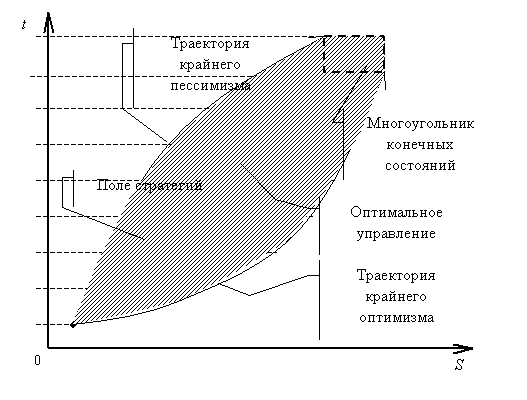
Рис. 6.  Пример построения оптимальной стратегии.

В учебнике [4] доктор экономических наук, профессор Ю.А. Маленков пишет: «Применяя научные методы моделирования стратегий, руководители компаний получают новые возможности быстро и эффективно определять сильные и слабые стороны своих фирм, выйти на новый уровень конкурентоспособности, увеличить прибыль и эффективность, устранить препятствия, мешающие формированию команд эффективных менеджеров, оценить уровень развития своих менеджеров, развивать механизмы внутренней конкуренции».  Надеемся, что пространственно – временные диаграммы будут способствовать решению этих задач.

Литература:

1.Глобальная трансформация: экономика, бизнес, социум: коллективная монография. / Автоном. некоммерч. орг. высш. проф. образования «Владим. ин – т бизнеса». – Владимир: ВИБ, 2012.

2. Крылов В.Е. Пространственно-временные диаграммы в стратегическом управлении социально-экономическими системами // Динамика сложных систем. 2012, № 4, т.6, С. 36 – 43.

3. Андрианов А.Ю. Стратегические проблемы социального развития муниципального образования // Актуальные проблемы менеджмента: формирование эффективных систем и процессов стратегического управления: материалы научно – практической конференции. Санкт – петербург, 14 декабря 2012 г. СПб.: ОЦЭиМ, 2013 – 220 с., с.с. 64 – 66.

4. Маленков Ю.А. Стратегический менеджмент: учеб. – М.: Проспект, 2009. – 224 с.