Андриенко В.М., Будорацкая Т.Л.

Главные компоненты динамики фондового рынка

Одесский национальный политехнический университет, г. Одесса, Украина

ГЛАВНЫЕ КОМПОНЕНТЫ ДИНАМИКИ ФОНДОВОГО РЫНКА

Задача построения  математических моделей, позволяющих лучше понять структуру и поведение рынка, как единого целого, так и его составляющих, является весьма актуальной для исследователей и практиков.Острота и научная значимость решения данной проблемы в наибольшей степени очевидна применительно к молодым развивающимся фондовым рынкам, специфика которых не всегда в полной мере учитывается имеющимся инструментарием. В данной работе применен многомерный статистический анализ для  оценки влияния макроэкономических показателей на фондовый индекс ПФТС.

В работе [1] показано, что  динамика индекса ПФТС (Первая Фондовая Торговая Система) пределяется множеством  совокупно действующих причин, то есть индекс  имеет многопризнаковую природу. Надежное отображение его в экономико- математических моделях возможно при условии учета комплекса присущих ему наиболее существенных характеристик. Для построения такой модели целесообразно использовать методы многомерного статистического анализа.  В настоящее время накоплен некоторый опыт в этом направлении. Например, в опубликованных ранее работах [2-4], рассмотрены многомерные  модели динамики различных фондовых параметров. В данной статье представлена многофакторная модель, отражающая взаимосвязь между фондовым индексом  ПФТС и основными макроэкономическими показателями.

В качестве факторов, влияющих на динамику фондового рынка, используются следующие  показатели: -  курс гривны к 100 долларам;   - индекс роста промышленного производства в % к предыдущему периоду ;  - индекс потребительских цен в % к предыдущему периоду ;  - инвестиции в основной капитал в % к предыдущему периоду ; - производство с/х продукции в % к предыдущему периоду; - экспорт в % к предыдущему периоду; - импорт в % к предыдущему периоду.

Учитывая тот факт, что  значения  индекса ПФТС  и некоторых макроэкономических показателей (например, курс гривны) коррелируют между собой на продолжительном  интервале времени, здесь взяты годовые значения всех показателей за 1997-2012г.г. Кроме того, для годовых значений выполняется основное требование к исходным данным для многомерного анализа, которое  заключается в том, что эти данные должны подчиняться многомерному нормальному распределению. Исходные данные официального сайта Госстата Украины [5] приведены в Таблице 1 (данных, - число  показателей(признаков)).

Таблица 1

Для сопоставимости показателей, исходные данные необходимо нормировать. Тогда основная модель факторного анализа имеет вид:

, (1)

j =, - нормированный  j-й признак (величина случайная); –  общие факторы (величины случайные, нормально распределенные);  uj – характерный фактор; aj1, aj2, …, ajp – факторные нагрузки, характеризующие существенность влияния каждого общего фактора; dj – нагрузка характерного фактора. Дисперсии  признаков  в силу нормирования равны единице, а средние значения равны нулю. Общие  факторы имеют существенное значение для анализа всех признаков. Характерные  факторы показывают, что он относится только к данному -му признаку. Основная задача факторного анализа – определить факторные нагрузки и собственные числа корреляционной матрицы.  

Из числа методов, позволяющих обобщать значения элементарных признаков, алгоритмически наиболее простым является метод главных компонент [6]. Однако, вычислительные процедуры метода главных компонент  достаточно трудоемки, поэтому расчеты проводились в Microsoft Excel с использованием надстроек «Анализ данных» и Attestat [7,8]. Получены следующие результаты:

Таблица 2.

Матрица факторных нагрузок 

Собственные числа корреляционной матрицы равны (Таблица 2):

Таким образом, первая главная компонента  объясняет примерно 3,4543/7=49,347049% всей вариации, вторая главная компонента  объясняет 1,6107/7= 23,009423%,  -  1,0212/7= 14,5888 14%.  Первые три главных компоненты учитывают примерно 87% суммарной дисперсии. Все семь компонент учитывают 100% дисперсии.

Статистическая оценка надежности решений методом главных компонент предполагает подтверждение значимости корреляционной матрицы и достаточности числа обобщенных факторов соответственно по критерию Уилкса и критерию Бартлетта [9].  В рассматриваемой задаче корреляционная матрица значима и в модели следует оставить  главных компоненты.

Компоненты можно интерпретировать следующим образом. В матрице факторных нагрузок первый столбец соответствует первой компоненте. Здесь достаточно высокими являются вклады показателей:  - индекс роста промышленного производства,  - инвестиции в основной капитал;  - соответственно экспорт и импорт товаров.  Первую компоненту  можно считать обобщенным фактором экономического потенциала. Второй столбец соответствует второй компоненте , наибольший вклад дают показатели  – курс гривны к доллару и  - инфляция, следовательно   -  обобщенный фактор стабильности  экономики.  Третью компоненту   и четвертую  можно считать соответственно:  обобщенный  фактор развития  аграрного сектора и  стабильность гривны по отношению к  доллару.

Теперь определим зависимость индекса ПФТС от выделенных факторов. Применим классический регрессионный анализ [10]. Данные для анализа приведены в Таблице 3. Статистические данные по ПФТС взяты на официальном сайте Национальной комиссии по ценным бумагам и фондовому рынку (НКГБФР) [11] .

Таблица 3.

Исходные данные регрессионного анализа

Второй и третий столбцы таблицы содержат исходные  и стандартизованные  значения индекса ПФТС. В остальных столбцах помещена матрица -

транспонированная матрица значений факторов.  Матрицу  ,  находят из соотношения:

(3)

Связь между переменной  и  главными компонентами  выразим в виде линейной регрессионной модели

, (4)

где   - параметры регрессии, - случайная ошибка наблюдений, нормально распределенная с параметрами  .

При построении регрессионной модели возникает вопрос об оптимальном составе главных компонент. На практике рекомендуется первоначально получить модель с учетом всех  главных компонент, затем последовательно исключать главные компоненты с наименьшим значением [6]. Выводы о качестве регрессионных уравнений делают по данным статистических критериев: - критерия Фишера о значимости модели, -критерия Стьюдента о существенности параметров модели,  - множественных коэффициентов корреляции и детерминации. Регрессионный анализ показал, что перечисленным критериям удовлетворяет регрессионная модель для шести факторов (Таблица 4). В этой модели значимыми являются параметры  и , следовательно, в уравнение регрессии должны быть включены факторы .

Таблица 4

Результат регрессионного анализа

Значение   – статистики равно 4,0920 , == 3,37 - квантиль распределения Фишера,   = =1,860 - квантиль распределения Стьюдента, где  - уровень значимости,  - число независимых переменных, - число данных; уровень значимости принят равным .

Таким образом, факторная модель имеет вид:

(5)

Переходя к исходной переменной , окончательно получим

(6)

Таким образом, на динамику индекса ПФТС оказывают влияние фактор экономической стабильности и фактор стабильности гривны по отношению к доллару.

Модель может быть статистически значима, но не адекватна. Если модель адекватна, то в силу предположений остатки  являются реализациями случайных ошибок наблюдений, которые независимы, имеют нормальное распределение с параметрами . В данном случае , а среднеквадратическое отклонение = 0,69. Эмпирическое распределение ошибок близко к нормальному по критерию Пирсона -на уровне . Следовательно, можно считать модель адекватной.

На Рис.1 представлен график фактических и предсказанных по уравнению (7) значений  ПФТС.  Черным цветом обозначены фактические значения, серым цветом – предсказанные.

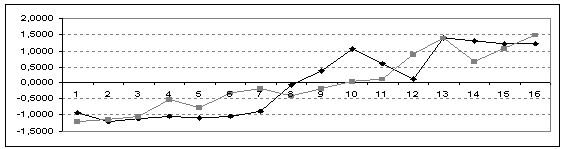
Рис.1. Результат моделирования.

Прогнозные значения достаточно близки к фактическим  значениям и практически полностью отражают тенденцию динамики индекса. Таким образом, построенную регрессионную модель можно использовать для оценки влияния макроэкономических  показателей на динамику  индекса ПФТС. Для

этого на основании (3) выразим факторы через исходные переменные

, (7)

где  - элементы -го столбца для -ой главной компоненты матрицы факторных нагрузок . Далее, учитывая вклад  переменных   в каждый фактор, получим следующую зависимость

(8)

В итоге, в соответствии с (8) можно считать, что фондовый индекс ПФТС зависит в настоящее время от двух показателей: курса гривны по отношению к

доллару и индекса потребительских цен.

В результате применения методов многофакторного анализа удалось выделить макроэкономические показатели, наиболее существенно влияющие на динамику  рыночного индекса. Полученная регрессионная модель позволяет прогнозировать значения индекса ПФТС:

1) рост курса  гривны к доллару на один пункт может привести ПФТС к увеличению на 185,92 пункта;

2) рост инфляции на 1% приводит к снижению  индекса на 34, 32 пункта.

Следует отметить, что ситуацию, которую отражает модель, нельзя считать экономически удовлетворительной. Фондовый рынок и инфляция движутся разнонаправленно, в то время как в развитых странах наблюдается противоположная ситуация. Движения фондового рынка и инфляции совпадают (кроме случаев неожиданной инфляции).  Рост фондового рынка только за счет роста курса гривны по отношению к иностранной валюте также является скорее негативным явлением. Более естественным положением было бы влияние индекса промышленного производства.  Данные обстоятельства свидетельствуют о нестабильности  экономики и инертности фондового рынка. 

Полученные результаты могут представлять интерес для специалистов по макроэкономическому анализу и прогнозированию развития фондового сектора национальной экономики, а также использованы в работе компаний, занимающихся инвестиционной деятельностью на фондовых рынках.

Литература

1. Андриенко В.М. Идентификация модели динамики Украинского фондового индекса ПФТС/Технологический аудит и резервы производства, №6/4(8), 2012.-С.7-8.

2. Никонов О.И., Фирсов А.А. Применение факторного анализа для моделирования доходности российского фондового рынка/Вестник УГТУ-УПИ, №3, 2009.- С.111-5. 5.

3. Кукушкина В.В. Проверка применимости факторной модели и модели АРТ для моделирования российского рынка акций/Российская экономика: взгляд молодых исследователей (сборник рефератов) − Москва: ИЭПП, 2006. -С.82-88.

4. Олейник А.Б. /Бизнесинформ, №7, 2010.-С.1-9.

5. Отчеты Госстата Украины/Интернет-ресурс. – Режим доступа: www/ URL: http://www.ukrstat.gov.ua. – Загл. с экрана.

6. Л.А.Сошникова, В.Н.Тамашевич, Г.Уебе, М.Шефер Многомерный статистический анализ в экономике/ Под ред. В.Н.Тамашевича-М.:ЮНИТИ, 1999.- 598с.

7. Пикуза В., Геращенко А. Экономические и финансовые расчеты в EXCEL: Самоучитель.-СПб. :Издат. группа BHV, 2003.-400с.

8. Гайдышев И.П.Моделирование стохастических и детерминированных систем: Руководство пользователя программы AtteStat /Интернет-ресурс. –  Режим доступа: www/ URL:http://attestatsoft.narod.ru - Загл. с экрана.

9. К. Иберла. Факторный анализ.-М.-Статистика,1980-397с.

10.  Елисеева И.И. Эконометрика: учебник/И..И.Елисеева, С.В.Курышева,

Т.В.Костеева. М.: Финансы и статистика, 2007.-456с.

11.  Отчеты Национальной комиссии по ценным бумагам и фондовому рынку за 2000-2012гг. /Интернет-ресурс. – Режим доступа: www/ URL: http:// ssmc.gov.ua. – Загл. с экрана.