Игнатьев В.М.

Игровой выбор объекта

Южно-Российский государственный технический университет (НПИ)

Рассмотрим задачу выбора объекта в условиях полной неопределённости, когда не заданы условия предпочтения одного показателя над другим показателем [1]. Число показателей, которые характеризуют альтернативные объекты, равно m. Число рассматриваемых альтернативных объектов обозначим через n. Значение j-го показателя у i-ого объекта равно (1)

где Xij – величина показателя; i – индекс объекта; j – индекс показателя.

Показатели альтернативных объектов образуют матрицу показателей X (1). Показатели имеют различную размерность, физическую природу и выражаются различными числовыми значениями. Для сравнения всех показателей между собой желательно иметь показатели одинаковой размерности или иметь безразмерные величины со значениями от 0 до 1, которые называют рандомизированными (указывающие не на случайность получения показателя, а на то, что он принимает значение от 0 до 1). Стратегия выбора объекта по определенному показателю бывает заранее известна, поэтому значения показателей можно привести к рандомизированному виду с помощью следующих формул.

Для показателя с положительным эффектом действия на объект, когда желательно иметь максимальное его значение, показатель рассчитывается по формуле: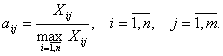 (2)

Для показателя с отрицательным эффектом действия на объект, когда желательно иметь минимальное его значение, производит вычисление по формуле: 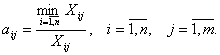(3)

Значения матрицы , полученной с помощью формул преобразования (2) и (3), принимают значения отрезка [0,1] и рассматриваются в дальнейшем как вероятности событий игры. Весовые коэффициенты каждого показателя объекта qj, j =  можно определить с использованием метода экспертного оценивания по k-бальной шкале j-го показателя. Весовые коэффициенты показателя вычисляются по формуле:

Аддитивный критерий оценки эффективности объекта с весовыми коэффициентами рассчитывается по формуле: (5)

Среднее значение критерия (5) называют критерием Лапласа

Когда суммарный уровень снижения показателя или показателей объекта не превышает суммарного уровня увеличения критерия объекта, т. е. для более значительного влияния показателей на значение критерия предлагается мультипликативный критерий эффективности объекта: (6)

Значения показателей отрицательного эффекта должны быть не равными нулю, в противном случае критерий (6) будет равен нулю. Можно объединить аддитивный критерий (4) и мультипликативный критерий (6) в один обобщенный критерий: (7)

где g - коэффициент влияния аддитивной части критерия, при 0 £ g £ 1.

Относительный разброс рандомизированного значения каждого показателя aij сильно влияет на величину критерия эффективности для оценки при выборе объекта, вычисляемую по формулам (5)¸(7).

для показателей с положительным эффектом cij = ;

для показателей с отрицательным эффектом cij = .

Возведение ранжированных значений показателей в соответствующие степени позволяет усугубить значения цены игры сij.

Оптимальная стратегия выбора объекта или оценка игры может определяться: – аддитивным критерием: P1 = (8)

– мультипликативным критерием: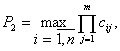 (9)

– критерием Вальда: (10)

– критерием Cэвиджа: (11)

– критерием риска Гурвица:  (12)

где l - вес минимального значения показателя цены игры, 0 £ l £ 1.

В критериях игры (8), (9) при выборе предпочитаемого объекта используются значения только одного показателя, одного элемента цены игры. Согласно критерию (10) игра ведётся как с агрессивным противником, делающим все для того, чтобы помешать достигнуть успеха.

Критерий Вальда олицетворяет позицию крайнего пессимизма. Если руководствоваться этим критерием, надо всегда ориентироваться на худшие условия, зная наверняка, что хуже этого не будет. Критерий Вальда называют перестраховочным. Критерий Сэвиджа (11) указывает, что значимость цены игры является величиной ущерба или риска при выборе объекта. Величина ущерба не превосходит его максимального значения по всем рассматриваемым системам. Критерий Сэвиджа называют критерием минимального риска, т.е. критерий ориентируется на величину риска. Сущность оптимизации по критерию Сэвиджа - возможность избежать большого риска при принятии решения. С помощью критерия Гурвица (12) оценивается взвешенное среднее из суммы минимального и максимального показателей, которые характеризует объект. Критерий Гурвица (12) является промежуточным между критериями успеха (8), (9) и критериями риска (10), (11). Критерий Гурвица называют критерием пессимизма-оптимизма. Значения выбора объекта по этому критерию совпадает с выбором критериев успеха (аддитивного, мультипликативного) или с выбором критериев Вальда  и Гурвица. Выбор критерия принятия решения или построения нового критерия является субъективным фактом, но всегда позволяет оценить объект по совокупности его показателей.

В качестве одного из эффективных критериев выбора объекта предлагается использовать Эвклидово расстояние до идеального объекта. Идеальный объект – объект, имеющий все координаты равные единицы. Рандомизированная матрица Сэвиджа представляет собой покоординатное расстояние от точки объекта до идеального объекта, где каждая координата меньше единицы. Предлагаемый критерий имеет следующий вид

P6 = 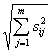, где sij – элемент матрицы Сэвиджа.

Критерий P6 работает в m-мерном пространстве параметров выбора.

Использую матрицу С в качестве исходной для выбора объекта, можно применить метод главных компонент из прикладной многомерной статистики для построения критерия выбора, который является линейной комбинацией коэффициентов собственных векторов латентных показателей, построенных на ковариационной матрице [2].

Выбор критерия принятия решения или построения нового критерия является субъективным фактом, но всегда позволяет оценить объект по совокупности его показателей.

Решение задачи выбора объекта игровым методом позволяет исключить некоторые показатели, характеризующие объекты, оценить влияние количественных и качественных показателей, указать условия предпочтения между показателями, т. е. не только выбрать объект, но и сформировать эффективную систему показателей. Игра по выбору объекта выделяет значимость показателя, позволяет упорядочить показатели по степени значимости. Значимость показателей, выраженная весовыми коэффициентами, определяемыми по (4), позволяет производить выбор в условиях частичной неопределенности.

Задачу выбора объекта следует решать в следующей последовательности: выбор в условиях неопределенности, упорядочение показателей и использование критериев эффективности, ввод уточненных цен игры и выбор в условиях частичной определенности. По предложенной методике были проведены выбор показателей систем хозяйственного и системного водопользования, также  комплексов машин и оборудования, используемых при строительстве и реконструкции оросительных систем [3].

Литература:

1. Ларичев О.Н. Теория и методы принятия решения, а также Хроника событий в Волшебных странах: учебник / О.Н. Ларичев. – М.: Логос, 2000. – 396 с.

2. Айвазян С.А. Основы эконометрики: учебник для вузов в 2-х т. / С.А. Айвазян. – М.: ЮНИТИ-ДАНА, 2001. – Т. 2. – 432 с.

3. Волосухин В.А. Оптимизация решений в водохозяйственном строительстве / В.А. Волосухин, В.М. Игнатьев, И.А. Русин. – Ростов-на-Дону: Изд-во СКНЦВШ, 2003. – 136 с.