Зинченко А.Б., Батурина Е.С.
НМ-решение кооперативной игры с целочисленными побочными платежами
Южный федеральный университет. Россия
НМ-решение кооперативной игры с целочисленными
побочными платежами
Классическая кооперативная модель 
, где 
- конечное множество, 
- функция множества, предполагает возможность произвольного распределения между игроками полезности 
, которую может получить коалиция 
. Игра 
называется игрой с трансферабельной полезностью, ТП-игрой или игрой с побочными платежами. Основные концепции решения игры 
являются подмножествами множества дележей 
. Для сравнения дележей используется отношение доминирования. Дележ 
доминирует 
(
dom
), если существует такая коалиция 
, что 
, 
, и 
. D-ядро 
игры 
состоит из всех недоминируемых дележей. C-ядро 
выделяет дележи, удовлетворяющие минимальным требованиям всех собственных коалиций. НМ–решение 
определяется условиями: из 
следует 
¬dom
и 
¬dom
; для каждого 
существует такой дележ 
, что 
dom
. НМ-решение отражает норму поведения экономических агентов, но его трудно вычислить.
Предположение о трансферабельной полезности подходит не для всех экономических ситуаций, т.к. полезность (или ее денежный эквивалент) может состоять из неделимых единиц. В этом случае значения 
, 
, и дележи должны быть целыми числами. Кооперативная игра 
с множеством дележей 
, где 
- целочисленная решетка, и целочисленной характеристической функцией 
называется дискретной. Семейство дискретных игр с множеством агентов 
обозначим через 
. Примеры ситуаций, порождающих игры 
, приведены в [1]-[4]. С-ядро дискретной игры есть пересечение С-ядра соответствующей ТП-игры 
и целочисленной решетки 
. D-ядро 
и НМ–решение 
игры 
определяются с помощью отношения доминирования на множестве целочисленных дележей 
. Множество всех НМ-решений игры 
обозначим через 
.
Игры 
менее изучены, чем ТП-игры. Ссылки на работы по дискретным играм можно найти в [3]. Они, в основном, посвящены ядрам игры 
. В данной заметке описаны свойства НМ-решений.
Из определения игры 
следует, что она имеет конечное множество НМ-решений, каждое из которых содержит конечное множество дележей. Все НМ-решения дискретной игры находятся алгоритмами выделения ядер в графе доминирования 
, множество вершин которого состоит из дележей игры 
, а 
тогда и только тогда, когда дележ 
доминирует дележ 
. В дискретных аналогах некоторых ТП-игр, имеющих многочисленные семейства НМ-решений (монополистические ситуации), граф доминирования не содержит циклов, т.е. НМ-решение единственное. Из определений, результатов для ТП-игр и [1]-[4] следует:
- если игра 
несущественная (
), то НМ-решение единственное и состоит из одного дележа 
;
- если характеристическая функция 
простая (
, 
, 
), то семейство НМ-решений игры 
состоит из (возможно пустого) множества дележей 
;
- если НМ-решение ТП-игры содержит только целочисленные дележи, то оно является НМ-решением соответствующей дискретной игры;
- если игра 
имеет D-ядро и НМ-решения, то D-ядро содержится в любом НМ-решении;
- если D-ядро игры 
является ее НМ-решением, то НМ-решение единственное;
- если в игре 
существует С-ядро и НМ-решение, то D-ядро непустое, С-ядро содержится в D-ядре и в любом НМ-решении.
Пример 1. Дана кооперативная игра трех лиц с супераддитивной целочисленной характеристической функцией:
, 
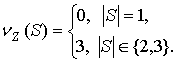(1)
В ТП-игре 
нет С-ядра и D-ядра, но существует НМ-решение 
. Соответствующая дискретная игра имеет непустое D-ядро 
, совпадающее со значением Шепли и N-ядром ТП-игры, но не имеет С-ядра и НМ-решений. Игра (1) является 0-формой игры, известной под названием "Мусор" [5]. Предполагается, что каждый из игроков имеет мешок с мусором, который он должен выбросить во дворе другого игрока. Нужно выяснить, смогут ли игроки договориться о размещении мусора. Согласно постановке, это дискретная игра и естественно было бы считать, что 
равно количеству мешков, принесенных игроками из 
во дворы участников коалиции 
. Однако в [5] вес коалиции 
рассматривается как трансферабельная "полезность" мешков, полученных агентами из 
("полезность" одного мешка равна (-1)). Интерпретация целочисленных решений игры (1) не вызывает затруднений. Но дробные дележи, содержащиеся в НМ-решении, не согласуются с постановкой проблемы.
Чтобы обойти трудности, связанные с дискретностью, при построении кооперативной модели в форме характеристической функции иногда вводят фиктивные делимости [6].
Особый интерес представляют кооперативные игры, в которых С-ядро является НМ-решением. Тогда оно доминирует все остальные дележи 
. Нерешенная до сих пор проблема классической кооперативной теории – каким условиям должна удовлетворять характеристическая функция, чтобы 
-ядро совпадало с НМ-решением – для дискретной игры (как показывает следующая теорема) разрешается просто, но такие игры не имеют практического значения.
Теорема 1. С-ядро дискретной игры является НМ-решением тогда и только тогда, когда оно совпадает с множеством всех дележей 
.
Пример 2. Дана дискретная игра трех лиц 0-редуцированной форме:
, 
, 
, nZ(1,3)=nZ(2,3)=nZ(N)=3. (2)
Она не имеет С-ядра, D-ядро состоит из трех дележей 
. НМ-решение является расширением D-ядра 
. Два дополнительных дележа доминируются дележами, не принадлежащими НМ-решению ((0,2,1)dom(2,1,0), (2,0,1)dom(1,2,0)), что снижает ценность этой концепции решения для игры (2).
Теорема 1 и пример 2 порождают новую проблему: при каких условиях D-ядро дискретной игры совпадает с НМ-решением? В следующей теореме сформулировано достаточное условие, при котором 
.
Теорема 2. Пусть 
- выпуклая функция, тогда D-ядро дискретной игры 
является ее единственным НМ-решением.
Известно, что в выпуклой ТП-игре С-ядро и D-ядро совпадают, поэтому теорема 2 аналогична результату, полученному для игр с трансферабельной полезностью. Заметим, что некоторые другие свойства выпуклой ТП-игры не переносятся на ее дискретный аналог. Например, равенство 
, справедливое даже для более широких, чем выпуклые, классов ТП-игр, в дискретной игре с выпуклой функцией 
выполняется только при совпадении С-ядра с множеством всех дележей [2].
Проведенные исследования показывают, что условия существования решений кооперативной игры, их свойства, сложность вычисления, соотношения между решениями могут сильно меняться при добавлении условия целочисленности дележей. В частности, проблема проверки существования С-ядра усложняется, а НМ-решения находятся проще.
Литература:
1. Зинченко А.Б., Мермельштейн Г.Г. Модель экономических ситуаций с дискретными платежами // Terra economicus. 2011. Т.9. №.3. С. 7-11.
2. Зинченко А.Б. Свойства ядер дискретной кооперативной игры. // Известия вузов. Северо-Кавказский регион. Естественные науки. 2009. № 2. С. 5-7.
3. Зинченко А.Б., Мермельштейн Г.Г. Сбалансированные и двойственно сбалансированные дискретные кооперативные игры // Экономический вестник Ростовского государственного университета. 2007. Т. 5. № 1. C. 109-115.
4. Zinchenko A.B., Oganjan L.S., Mermelshtejn G.G. Cooperative Side Payments Games with Restricted Transferability // Contributions to game theory and management. Collected papers of the Third International Conference «Game Theory and Management». 2010. V. III. P. 458-467.
5. Shapley L. S., Shubik M. On the core of an economic system with externalities // Amer. Econ. Rev. 1969. V. 59. P. 678-684.
6. Ju Y., Ruys P.H.M., Borm P. Compensating losses and sharing surpluses in project-allocation situations // Discussion paper. № 2004-37. university. P. 1-17.