Яговкина Е.Н., Майдан Д.А.

Методика экспертных оценок для выбора марки керамогранита

Самарский государственный технический университет, Россия

Методика экспертных оценок для выбора марки керамогранита

Керамогранит (керамический гранит) – это искусственный отделочный материал. Производится прессованием смеси глины и гранитных крошек при давлении 400-500 г/см2, с последующим обжигом при температуре 1200-1300 °C. Используется два вида глины – одна более пластична, богата иллитом, другая менее пластична, богата каолинитом [1, 2].

Внешне керамогранит напоминает натуральный камень, с присущими ему крапинками, разводами, всполохами. Но керамогранит окрашен гораздо равномернее, цветные вкрапления расположены более равномерно, чем у натурального камня. Еще одно отличие от натурального камня – на поверхности керамогранита нет трещин и крупных вкраплений другого цвета. Рисунок облицованной поверхности однороднее, без беспорядочных полос и пятен (чего практически нельзя достичь при облицовке натуральным камнем). Кроме этого, производится однотонный керамогранит. Также существует керамогранит под антик, с рельефной или глазурованной поверхностью.

Методика экспертных оценок. К опросу экспертов (специально привлекаемых компетентных лиц) прибегают обычно в тех случаях, когда надежный ответ на интересующий важный вопрос (или совокупность вопросов) не может быть получен другими более объективными методами (например, методами экспериментального или теоретического исследования). При выборе (товароведной экспертизе) керамогранита опрос экспертов может оказаться весьма полезным или даже необходимым при решении следующих вопросов [3].

1. Определения состава совокупности {У, Os, К, Ок} исходных данных:

- У={У1 … ,Уp} – совокупность условий;

- К ={к1, … ,кm} – состав совокупности (вектора) показателей качества керамогранита;

- Ok ={Ok1, … ,Okr} – совокупность ограничений, накладываемых на показатели качества.

2. Обоснования количественной формулировки некоторых из ограничении Os, Ок, например выбора максимально допустимых значении к1M, … ,кmM показателей качества.

3. Выбора вида критерия предпочтения.

4. Выбора значений параметров критерия предпочтения, например значений весов c1, … ,cm, входящих в результирующую целевую функцию.

5. Выбора лучшего вида керамогранита из конечного числа строго допустимых S1, …,Sj, … ,Sn в условиях, когда каждый вид Sj характеризуется вектором (совокупностью) Кj ={к1j, … ,кmj} показателей качества.

Различные методы опроса экспертов в большинстве случаев сводятся к следующему [3].

1. Составляется таблица экспертного опроса, которую должны заполнить эксперты, и пояснения к ней, указывающие, как следует заполнять таблицу и какие при этом учитывать факторы.

2. Выбирается состав экспертов из числа специалистов, имеющих большой опыт разработки и (или) эксплуатации аналогичных или близких по характеру систем. При этом важно обеспечить независимость высказываний экспертов.

3. Эксперты заполняют таблицу опроса, например, проставляют оценки в баллах по стобальной шкале каждой предложенной для оценки системе или каждому предложенному решению.

4. Производится статистическая обработка данных опроса, имеющая целью:

а) определить средние статистические значения оценок, например средние баллы, присваиваемые каждому виду керамогранита;

б) определить степень надежности полученных оценок.

О надежности оценок судят по таким статистическим характеристикам, которые описывают разброс оценок отдельных экспертов и групп экспертов или, что эквивалентно, степень согласованности (совпадения) оценок [3].

Эксперты 1, 2, ..., j, ..., N должны дать оценки решениям P1, …,Pi, … ,Pm. При этом разброс оценок, даваемых N экспертами решению Pi (виду керамгранита Si, весовому коэффициенту ci и т. п.), характеризуется величиной вариации

где ; и  - среднее значение и дисперсия оценки, данной решению Pi; (усреднение производится по N решениям экспертов).

Степень согласованности оценок, даваемых по совокупности всех оцениваемых решений, характеризуют так называемым коэффициентом конкордации (согласия) W и соответствующим уровнем значимости . Здесь , а  есть вероятность того, что согласованность мнений (оценок), характеризуемая данным коэффициентом конкордации W, есть случайное совпадение. Чем больше W и чем меньше , тем более согласованными (надежными) являются оценки. Обычно согласованность считают удовлетворительной, если , , и хорошей, если  и .

Степень согласованности решений двух групп (I и II) экспертов  характеризуется коэффициентом ранговой корреляции   - чем ближе  к единице, тем более согласованы решения. Обычно согласованность считается удовлетворительной при  и хорошей при .

Для вычисления значений W,  и  приходится предварительно находить ранги R1, …,Ri, … ,Rm соответствующих решений P1, …,Pi, … ,Pm.

Если ранжирование элементов некоторого множества не может быть произведено непосредственно по количественному признаку, то оно может быть произведено непосредственно по качественному признаку («лучше» - «хуже») или в два этапа: на первом каждому элементу экспертом дается оценка в баллах, например по стобалльной шкале - чем «лучше» оцениваемый элемент, тем выше его оценка в баллах. На втором происходит ранжирование элементов по степени убывания присвоенных баллов - первый ранг присваивается элементу, получившему наивысший балл, второй ранг - элементу, получившему следующий по величине балл и т. д.

Первый метод ранжирования является непосредственным, а второй - по результатам экспертных оценок. В общем случае оба этих метода могут давать несколько различающиеся результаты.

Если несколько сравниваемых элементов имеют одинаковый количественный (или качественный) признак, используемый для ранжирования, то им присваивается одинаковый ранг, равный среднему арифметическому.

Формулы, позволяющие вычислить значения параметров W,  и , характеризующих согласованность оценок экспертов [3]:

где

Rji - ранг, присвоенный решению Pi j-тым экспертом;

Si - сумма рангов, присвоенных решению Pi всеми экспертами;

среднее значение суммы рангов, где усреднение производится по всем m решениям;

где Lj - число групп решений с совпавшими рангами в совокупности решений j-го эксперта;

l - номер группы (с совпавшими рангами);

tjl - число совпавших решений j-го эксперта в группе номера l.

Величина уровня значимости  определяется по таблицам распределения случайной величины  с (N - 1) степенями свободы, где

Коэффициент ранговой корреляции определяется по формуле

где  и  - ранги, присвоенные решению Pi (соответственно I и II группой экспертов).

Путем вычисления и оценки значений величин , W,  и , возможно [3]:

- определить надежность полученных в результате экспертных оценок значений;

- проверить согласованность мнений различных экспертов и различных групп экспертов (например, специалистов по системным исследованиям и специалистов по эксплуатации);

- выяснить причины возможной ненадежности полученных оценок, например, поочередно исключая мнение каждого эксперта и вычисляя значения представленных выше величин, выявить эксперта (ряд экспертов), мнение которого значительно отличается от мнения остальной (большей) части экспертов.

Для экспертной оценки уже полученных (рассчитанных) результатов каждому варианту назначаются ранги (лучшей марке керамогранита присваивается ранг 1). При этом если мнение экспертов существенно отличается от результатов расчетов, необходима корректировка исходных данных, например ограничений на показатели качества керамогранита.

При опросе экспертов могут возникнуть сложности задания оценки в баллах для каждого предложенного решения, для человека гораздо проще провести попарное, чем групповое сравнение элементов (одно решение «лучше» или «хуже» другого).

В этом случае применяется методика, основанная на методе попарных сравнений [3, 4]. Результаты сравнения оформляются в виде таблицы 1, имеющей вид квадратной матрицы ||B||.

Таблица 1

Матрица результатов попарных сравнений

Оценка результатов парных сравнений Bij производятся на основе предлагаемых в таблице 2 шкал качественных и количественных оценок предпочтительности элементов по отношению друг к другу.

Таблица 2

Шкалы качественных и количественных оценок предпочтительности элементов

Весовые коэффициенты элементов представляются в виде вектора Ν = < ν1, ν2,..., νL >, который удовлетворяет уравнению:

где || С || = || B || × || A || - матрица значений парных сравнений коэффициентов значимости элементов системы;

|| A || - матрица, сопряженная с || B || (их элементы связаны соотношением aij=bji);

Lmax - наибольшее собственное значение матрицы || С ||.

Алгоритм итерационной процедуры состоит в следующем [1-3].

1. Составление матрицы || A ||, сопряженной с|| B||.

2. Вычисление матрицы || C || = || B || × || A ||.

3. Составление характеристической матрицы || C – L || × ||E|| × || N || = 0,

где L - собственное значение матрицы || C ||, а || E || - единичная матрица.

4. Решение характеристического уравнения на основе рекуррентной процедуры

|| N(k)|| = || C || × || N(k-1) ||, где || N(0) || = || E ||, || N(k)|| - || N(k-1)|| < D - условие окончания итерационного процесса, а D - требуемая точность вычислений.

Вектор || N(k) || = < n1, n2, ... , n L> представляет собой искомые бальные оценки (весовые коэффициенты) каждого из решений Pi.

Таким образом, с использованием предложенной методики при товароведной экспертизе керамогранита возможно определить надежность полученных в результате экспертных оценок значений, проверить согласованность мнений различных экспертов, выяснить причины возможной ненадежности полученных оценок, а также производить бальную оценку нескольких видов товара с использованием метода попарных сравнений. Это позволяет рационально выбирать наиболее предпочтительную марку керамогранита в зависимости от производителя, места применения, ценовой категории и других показателей.

Литература

1. Яговкина, Е. Н. Основные виды и товароведные свойства керамогранита [CD-ROM] / Е. Н. Яговкина; науч. рук. Д. А. Майдан // Студенчество в науке — инновационный потенциал будущего: Тезисы докладов IV Всероссийской студенческой научно-практической конференции (Набережные Челны, 15 апреля 2011 г.). — Набережные Челны, 2011. — ISBN 978-5-91875-002-5.

2. Яговкина, Е. Н. Потребительские свойства керамогранита [CD-ROM] / Е.Н.Яговкина; науч. рук. Д. А. Майдан // Студенчество в науке — инновационный потенциал будущего: Тезисы докладов V Всероссийской студенческой научно-практической конференции (Набережные Челны, 13 апреля 2012 г.). — Набережные Челны, 2012. — ISBN 978-5-91875-012-4.

3. Яговкин, Н.Г Методология поддержки принятия решений при управлении интегративными крупномасштабными производственными системами [Текст] / Н.Г. Яговкин, В.И. Батищев. – Самара: Российская Академия наук, Самарский научный центр, 2008. – 288с.

4. Яговкина, Е.Н. Обеспечение качества поддержки принятия решений управления при управлении безопасностью жизнедеятельности [Текст] / Е.Н. Яговкина, Моссоулина Л.А., Чернышева Е.А. // ELPIT 2011. Экология и безопасность жизнедеятельности промышленно-транспортных комплексов: сб. трудов III Межд. экологического конгресса (V Межд. науч.-техн. конф.), Т.6, науч. симпозиум «Проблемы и инновационные решения в области инженерного обеспечения экологической и промышленной безопасности урбанизированных территорий» (Ч. 1). – Тольятти: ТГУ, 2011. – С.310-315.
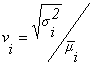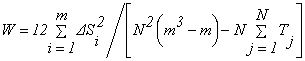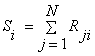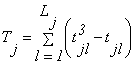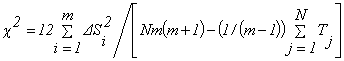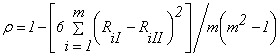