Меерсон А.Ю., Черняев А.П.

Точное решение дифференциального уравнения макроэкономической модели Харрода-Домара с переменным коэффициентом капиталоемкости прироста дохода

Точное решение дифференциального уравнения макроэкономической модели Харрода–Домара с переменным коэффициентом капиталоемкости прироста дохода

А.Ю. Меерсон, А.П.Черняев

В работе получено точное решение дифференциального уравнения макроэкономической модели Харрода–Домара с переменным коэффициентом капиталоемкости, зависящем от времени.

Дифференциальное уравнение модели Харрода-Домара с экзогенной динамикой потребения произвольного характера [1, 2] имеет вид

. (1)

Эта модель с непрерывным временем , описывающая динамику дохода , который рассматривается, как сумма потребления  и инвестиций . Экономика считается закрытой, поэтому чистый экспорт равен нулю, а государственные расходы в модели не выделяются. Основная предпосылка модели роста – скорость роста дохода пропорциональна инвестициям [3, с. 205]:, где - коэффициент капиталоемкости прироста дохода, или приростной капиталоемкости. До сих пор коэффициент капиталоемкости прироста дохода считался положительным и постоянным [4]

. (2)

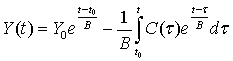.  (3)

Здесь предполагается выполненным начальное условие

. (4)

В настоящей работе предполагается, что

. (5)

При условиях (4) и (5) решение дифференциального уравнения (1) будет даваться формулой

которое и является основным содержанием данной работы. Простой проверкой нетрудно убедиться в том, что если , то из формулы (6) получается формула (3), т.к.

, ,

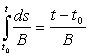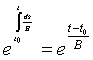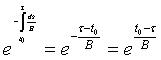
и

.

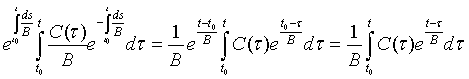Подставляя последние формулы в формулу (6) очевидно получаем (3).

Решение (6) дифференциального уравнения (1) при условиях (4) и (5) гораздо  важнее, решения (3) того же уравнения при условии (2), т.к. на практике условие (2) не может быть выполнено. Однако, решение (6) при условиях (4) и (5) важнее не только практически, но и теоретически, т.к. очень удобно для различных численных расчетов, которые невозможно осуществить зная лишь решение (3) уравнения (1) при условиях (2) и (3).

Работа выполнена при поддержке АВЦП «Развитие научного потенциала высшей школы», проекты № 2.1.1/11133 и 2.1.1/12968.

Список литературы

1. Меерсон А.Ю., Черняев А.П. Макроэкономическая модель Харрода-Домара с экзогенной динамикой потребения произвольного характера // Международная научно-практическая конференция «Инновации на основе информационных и коммуникационных технологий». Материалы международной научно-практической конференции «Инфо-2011». Симпозиум 4. Инновационные информационные и коммуникационные технологии в социальной среде. С. 437-439.

2. Меерсон А. Ю., Черняев А.П. Точное решение макроэкономической модели  Харрода-Домара с экзогенной динамикой объема потребления произвольного характера // Известия Российского экономического университета им. Г.В.Плеханова. 2011, № 1. С. 142-147.

3. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике: Учебник. – М.: МГУ им. М. В. Ломоносова, Издательство «ДИС», 1998 – 368 с.

4. Моделирование экономических процессов. Учебник для студентов вузов, обучающихся по специальностям экономики и управления (060000) / Под ред. М.В. Грачевой, Л.Н. Фадеевой, Ю.Н. Черемных. – М.: ЮНИТИ–ДАНА, 2005. –351 с.

5. Меерсон А. Ю., Черняев А.П. Особенности рабочего режима макроэкономической модели  Харрода-Домара с показателем потребления растущим в постоянном темпе // Вестник МГУП. М.: МГУП, 2012, № 3. С. 188-192.