Стрельцова Е.Д., Богомягкова И.В., Стрельцов В.С.

Стохастический автомат в переключаемой среде для управления межбюджетным регулированием

СТОХАСТИЧЕСКИЙ АВТОМАТ В ПЕРЕКЛЮЧАЕМОЙ СРЕДЕ ДЛЯ УПРАВЛЕНИЯ МЕЖБЮДЖЕТНЫМ

РЕГУЛИРОВАНИЕМ

В настоящее время особый интерес вызывает стоящая перед органами государственной власти субъектов РФ стратегическая задача выбора пропорций, в которых будут распределяться основные  средства межбюджетного регулирования.  В проводимых до настоящего времени исследованиях в основном уделялось внимание пассивной составляющей межбюджетного регулирования ─ перераспределению средств бюджета  вышестоящего уровня в бюджеты нижестоящего в форме дотаций, субсидий, субвенций. Функция стимулирования территорий  в их экономическом росте возложена на механизм  дополнительных отчислений от налогов и сборов, подлежащих  зачислению в региональный бюджет. Всё это имплицирует необходимость сосредоточения внимания на отношениях межбюджетного регулирования,  ориентируя их  на сокращение дотационности  бюджетов, повышение  самостоятельности, развитие инициативы. В [1] предложена автоматная экономико-математическая модель, позволяющая осуществлять долевое распределение налога одного вида между уровнями бюджетной системы. Для построенной модели определена структура автомата, состояниями которого являются величины долей  отчислений  денежных средств от уплаты налогов в порядке бюджетного регулирования, получены аналитические выражения для финальных вероятностей выбора автоматом своих состояний [1]. В реальной ситуации в процессе долевого распределения участвуют поступления от некоторого подмножества налогов, составленного из всего перечня налогов, участвующих при бюджетном регулировании. Для решения такой задачи авторами предложена математическая  модель поведения ранее описанного автомата  в переключаемых случайных средах. При этом для каждого вида налога  предлагается рассматривать свою отдельную случайную среду, вероятностные характеристики которой описываются вектором  , где оценка вероятности выигрыша автомата   в случайной среде, образованной  воздействиями поступлений от уплаты налога  вида , где  номера состояний автомата . Допустим, что в процессе долевого распределения доходов в порядке бюджетного регулирования участвуют  видов налогов: . Тогда имеем систему векторов , , описывающих вероятностные характеристики случайных сред:

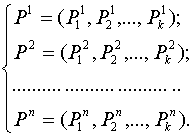
Переход к составной случайной среде приводит к следующему поведению автомата . Кроме переходов из одного состояния в другое состояние, автомат  может осуществлять переходы из одной случайной среды в другую. Переключаемую случайную среду обозначим . Автомат  находится в переключаемой случайной среде , если в каждый момент времени  он функционирует в одной из случайных сред  множества , где  множество индексов. Обозначим через  такое состояние системы «автомат – переключаемая среда», при котором автомат  находится в состоянии , а переключаемая среда – в состоянии  .  В качестве выходного воздействия на внешнюю среду системы «автомат – переключаемая среда» в момент времени в состоянии  примем величину , интерпретируемую как величина текущего запаса бюджета в условиях таких отчислений от уплаты налога вида , доля  которых составляет . При этом  если в момент  система находилась в состоянии  и произвела действие  , то в момент времени  это действие повлечёт за собой поступление входного сигнала  (т.е. «выигрыша») с вероятностью  и поступление входного сигнала  (т.е. «проигрыша» или «штрафа») с вероятностью . Если автомат в момент времени  находился в случайной среде , то в момент  он осуществит переход в случайную среду с вероятностью . Таким образом, рассматривается цепь Маркова, имеющая  состояний, матрица перехода которой из состояния  в состояние  обозначена , , .  Тогда оценка вероятности  перехода системы «автомат – переключаемая среда» из состояния  в состояние  определяется как  , где ,  – соответственно оценки вероятностей выигрышей и проигрышей системы «автомат – переключаемая среда» в состоянии ;  оценка вероятности перехода автомата  из состояния  в состояние  при поступлении входного сигнала , т.е. при «выигрыше»;  оценка вероятности перехода автомата  из состояния  в состояние  при поступлении входного сигнала , т.е. при «проигрыше» (или «штрафе»);  вероятность перехода автомата  из состояния  в состояние  при любом входном сигнале. 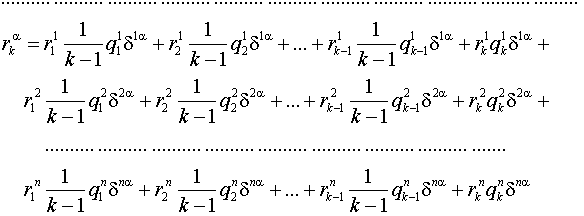Следовательно, вероятностные характеристики  и , ,  представляют собой оценки вероятностей соответственно дефицита и профицита, к которым приведёт пребывание  системы «автомат – переключаемая среда» в состоянии , интерпретируемом как доля отчислений денежных средств в бюджет нижестоящего уровня бюджетной системы РФ от уплаты налога вида  в порядке бюджетного регулирования.  Матрица перехода автомата  из одного состояния в другое в условиях действия случайной среды  имеет вид [1]:

.

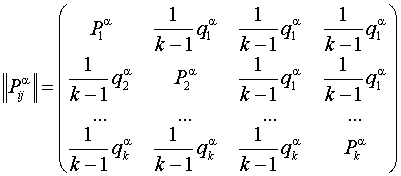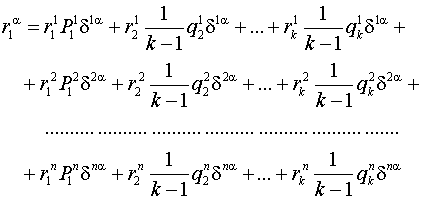
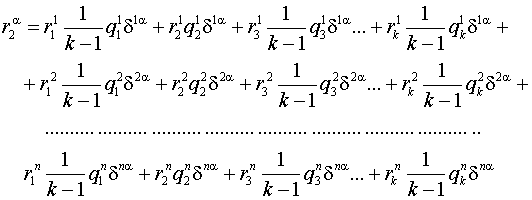
Примем, что составная вероятностная среда ,  переключается из одного состояния  в другое состояние  с одинаковой вероятностью  , , . Тогда на основе полученных уравнений для финальных вероятностей можно сделать вывод, что в условиях принятых допущений имеют место равенства: ; , …, .

Обозначим эти вероятности переменными соответственно . Решение составленных систем уравнений с учётом условия нормировки  позволило получить следующие выражения для финальных вероятностей пребывания системы «автомат-переключаемая среда» в своих состояниях:

………………………………………………………………………….

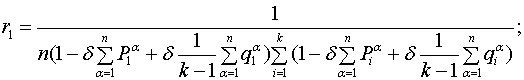
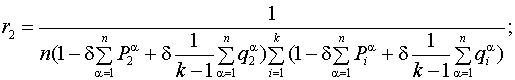
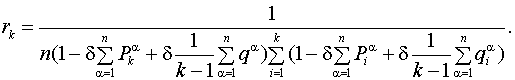
Для определения значений финальных вероятностей ,  на базе использования полученных выражений необходимо вычислить вероятности выигрышей  и проигрышей , ,  в каждом состоянии автомата. Для этой цели предлагается использование имитационной модели, описывающей  изменение величины остатков денежных средств в бюджете при случайном характере поступлений и расходований денежных средств.

Литература

1. Богомягкова И.В. Модель долевого распределения налогов в системе поддержки принятия решений по управлению межбюджетным регулированием //Научные ведомости Белгородского государственного университета (серия Информатика).-2010.-Выпуск 13/1