Трошина С.В.

Оптимизация инвестиционного портфеля при ограниченных вложениях

Оптимизация инвестиционного портфеля при ограниченных вложениях

Работа посвящена актуальному вопросу финансовой математики - построению динамической модели инвестиционной стратегии, учитывающей изменение во времени ставок доходности. Аналогичные модели рассматривались в [1,2], где так же, как и в представляемой работе, сформулированная задача инвестиционной деятельности формулируется как дискретная задача оптимального управления, для решения которой применяется принцип максимума Понтрягина.

Рассматривается конечный промежуток времени [0,T]. Предполагается, что инвестор планирует в каждый момент времени  ) вложить в безрисковые активы некоторую сумму, которая может быть немного больше или немного меньше величины  причем, сумма вложений во все активы в данный момент не должна превышать доход, полученный в этот же момент. Естественной целью инвестора является получение максимального дохода в конце срока при минимальных затратах.

Пусть инвестор вкладывает средства в  активов, имеющих ставку доходности  соответственно. Объем вложенных средств в  актив в момент  обозначим . Через  обозначим объем наращенного капитала по  активу за период от до .

Очевидно, динамика роста капитала определяется уравнениями:

.

При этом вложения должны быть сделаны так, чтобы достигал минимума критерий

где - положительные весовые коэффициенты.

Условие, ограничивающее величину вложений на каждом шаге, определяется неравенством

Введем обозначения:

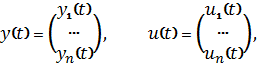
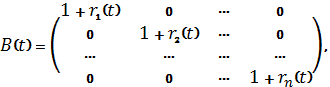
В результате сформулированная задача запишется в векторной форме:

(1)

, (2)

(3)

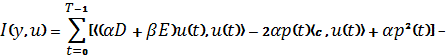
(4)

где  - дискретная траектория,  - дискретное управление,  - скалярное произведение векторов.

Таким образом, математическая модель рассматриваемой экономической задачи представляет собой дискретную задачу оптимального управления со смешанными ограничениями. Решение задачи (1)-(4) будем обозначать . Для получения необходимых условий оптимальности применим теорию Дубовицкого-Милютина [3].

В пространстве пар  рассмотрим конусы вариаций с вершиной в точке , соответствующие функционалу (4) и ограничениям, а также сопряженные к ним. Имеем следующие представления рассматриваемых конусов.

Конус запрещенных вариаций для функционала (4) с вершиной в точке :

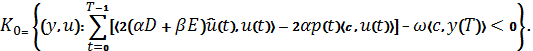
Сопряженный конус к конусу  состоит из функционалов вида:

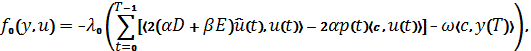
где .

Конус касательных направлений, соответствующий ограничениям (1), (2), совпадает с множеством пар , удовлетворяющих (1),(2), поэтому значение функционала  из сопряженного конуса на таких парах равно нулю.

Конус допустимых вариаций, соответствующий ограничению (3):

, , причем, конус  совпадает со всем пространством пар , если .

Сопряженный конус к конусу  состоит из функционалов вида:

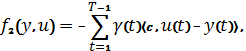
Если .

Теорема.

Если  - решение задачи (1)-(4), то существуют числа  и вектор-функция , для которых выполняется сопряженное уравнение

условие трансверсальности

и условие дополняющей нежесткости

При этом оптимальное управление определяется по формуле:

(5)

Здесь и далее знак * означает транспонирование.

Доказательство

Согласно теореме Дубовицкого-Милютина, существуют не равные одновременно нулю функционалы из сопряженных конусов, для которых имеет место уравнение Эйлера:

Для пары , удовлетворяющей уравнению (1) и условию (2), будем иметь:

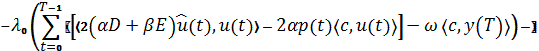
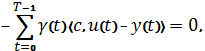
где .

Для произвольной вектор-функции  и пары , удовлетворяющей (1), имеем тождество

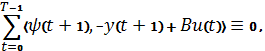
Сложим данное тождество с уравнением Эйлера, учитывая, что :

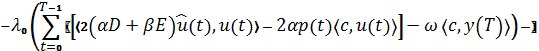
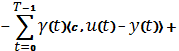
Выберем  так, чтобы выполнялось сопряженное уравнение  и условие трансверсальности

Тогда получим:

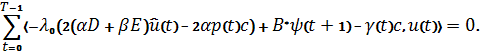
(6)

Так как для рассматриваемой задачи , и в (6) на  не накладывается никаких ограничений, то из последнего равенства для оптимального управления следует формула (5). Теорема доказана.

Можно показать, что полученные в данной теореме необходимые условия оптимальности являются также и достаточными. Таким образом, решение задачи оптимального управления (1)-(4) сводится к решению следующей краевой задачи (краевая задача принципа максимума):

  (7)

(8)

(9)

(10)

 (11)

В данных формулах

Обозначим:

Используя (7)-(10), найдем выражение  через

Аналогично из (5),(7)-(10):

Для нахождения множителей  из условия (11) будем иметь следующие уравнения.

Для

Для

.

Численная реализация.

Вычисления проводились в среде Mathcad для параметров

 Другие входные данные приведены в таблице 1. Таблице 2 содержит результаты вычислений.

Таблица 1

Таблица 2

Прибыль:

Литература:

1. Сидоров С.П., Трошина Н.Ю., Трошина С.В. Одна динамическая модель оптимизации инвестиционных вложений. //Аналитические и численные методы моделирования естественнонаучных  и социальных проблем. 5-ая Межд. науч.-техн. конф. Сб. статей. Пенза, 25-28 окт. 2010. 121-125.

2. Troshina S.V., Troshina N.Yu., Sidorov S.P. Discrete Dinamic Model of Portfolio Optimization with Risk-Free and Risk Assets. //Applitd Mathematical Sciences, Vol.7, 2013, no.20, 993-1004.

3. Дубовицкий А.Я., Милютин А.А. Задачи на экстремум при наличии ограничений. //ЖВМ и МФ. 1965. №3. 395-453.